MT【238】内心轨迹

标签：rac   轨迹   src   rri   分享   idt   jpg   http   技术分享   

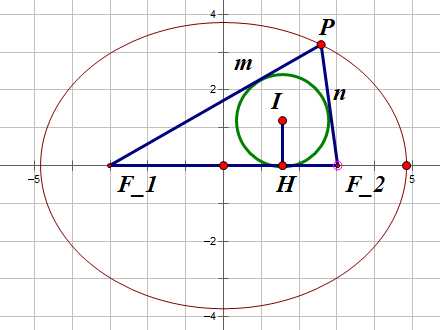
已知$F_1,F_2$为椭圆$C:\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$的左右焦点,点$P$在椭圆$C$上移动时,$\Delta{F_1PF_2}$
的内心$I$的轨迹方程为_____

分析:如图利用内心的向量结论得:$m\overrightarrow{IF_2}+n\overrightarrow{IF_1}+|F_1F_2|\overrightarrow{IP}=\overrightarrow{O}$
记$P(x_0,y_0),I(x,y)$容易知道$m+n=2a,m-n=2x$,
将坐标带入上式易得$y_0=3y,x_0=2x$代入$C:\dfrac{x_0^2}{4}+\dfrac{y_0^2}{3}=1$得$x^2+3y^2=1(y\ne0)$

MT【238】内心轨迹

标签：rac   轨迹   src   rri   分享   idt   jpg   http   技术分享   

原文地址：https://www.cnblogs.com/mathstudy/p/9863813.html