标签:etc problem size 范围 src i++ 期望dp str printf
这是写第一个概率期望dp。
一般看见这种题就想暴力了,看一下数据范围,暴力应该还是挺好想的吧。
24分
注意到有6个测试点m=0m=0,则说明不能提出申请,那么只需要求出全图的两两之间的最短路,路径唯一确定。
52分
注意到另外有7个测试点m=1m=1,只能提出一次申请。我们可以直接枚举在哪里提出申请,再与不申请的时候取一个min就可以了。
76分
注意到还有6个测试点m=2m=2,只能提出两次申请,暴力枚举哪两个点申请即可。
80分
其实我们并不需要分那么多类情况讨论,考虑直接爆搜,在每个点是否提出申请,最后暴力计算贡献。因为这样的复杂度是C(n ,m)?的,所以m<=2和n<=10是完全没有问题的,直接可以用搜索拿到80分。
接下来就让我们看一下正解,概率期望dp + floyd
我们设f[i][j][0/1]:表示前 i 门课程,已经申请 j 间教室,这间教室有没有申请的最小的期望值 状态转移方程:
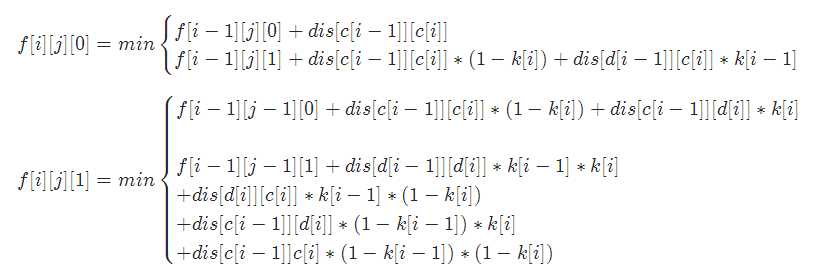
其实刚开始看到转移方程的我是崩溃的。但是转移挺好想的,很顺(舒服)。
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int maxn = 2005; const int inf = 0x7fffffff; inline int read(){ int f = 1 , x = 0; char ch = getchar(); while(ch > ‘9‘ || ch < ‘0‘){ if(ch == ‘-‘) f = -1; ch = getchar(); } while(ch >= ‘0‘ && ch <= ‘9‘){ x = x * 10 + ch - ‘0‘; ch = getchar(); } return x * f; } int n,m,v,e,x,y,z; int c[maxn],d[maxn]; double k[maxn],f[maxn][maxn][2],ans; int dis[maxn][maxn]; void floyd(){ for(int k=1;k<=v;k++) for(int i=1;i<=v;i++) for(int j=1;j<=v;j++) if(i != j && j != k && i != k) if(dis[i][k] != inf && dis[k][j] != inf) if(dis[i][j] > dis[i][k] + dis[k][j]) dis[i][j] = dis[i][k] + dis[k][j]; } int main(){ //freopen("hjs.in","r",stdin); n = read(); m = read(); v = read(); e = read(); for(int i=1;i<=n;i++) c[i] = read(); for(int i=1;i<=n;i++) d[i] = read(); for(int i=1;i<=n;i++) scanf("%lf",&k[i]); for(int i=1;i<=v;i++) for(int j=1;j<=v;j++) dis[i][j] = inf; for(int i=1;i<=e;i++){ x = read(); y = read(); z = read(); if(dis[x][y] == inf){ dis[x][y] = z; dis[y][x] = z; } else{ dis[x][y] = min(dis[x][y] , z); dis[y][x] = min(dis[y][x] , z); } } for(int i=1;i<=v;i++) dis[i][i] = 0; floyd(); for(int i=1;i<=n;i++) for(int j=0;j<=m;j++) f[i][j][0] = f[i][j][1] = inf; f[1][0][0] = f[1][1][1] = 0; for(int i=2;i<=n;i++){ //f[i][0][0] = f[i-1][0][0] + dis[c[i-1]][c[i]]; //表示一直都不换的消耗 for(int j=0;j<=min(i , m);j++){ double minl = f[i-1][j][0] + dis[c[i-1]][c[i]]; minl = min(minl , f[i-1][j][1] + dis[c[i-1]][c[i]] * (1 - k[i-1]) + dis[d[i-1]][c[i]] * k[i-1]); f[i][j][0] = min(f[i][j][0] , minl); if(j >= 1){ minl = f[i-1][j-1][0] + dis[c[i-1]][c[i]] * (1 - k[i]) + dis[c[i-1]][d[i]] * k[i]; minl = min(minl , f[i-1][j-1][1] + dis[d[i-1]][d[i]] * k[i-1] * k[i] + dis[d[i-1]][c[i]] * k[i-1] * (1 - k[i]) + dis[c[i-1]][d[i]] * (1 - k[i-1]) * k[i] + dis[c[i-1]][c[i]] * (1 - k[i-1]) * (1 - k[i])); f[i][j][1] = min(f[i][j][1] , minl); } } } ans = inf; for(int i=0;i<=m;i++){ ans = min(ans , min(f[n][i][0] , f[n][i][1])); } printf("%.2lf",ans); return 0; }
妈呀,终于写完了。。
标签:etc problem size 范围 src i++ 期望dp str printf
原文地址:https://www.cnblogs.com/Stephen-F/p/9866374.html