标签:mit 答案 修改 https math code limit rip 部分
给出一个序列 \(a[1...n]\) ,求构造一个 \(b[1...n]\) ,满足\(b_{i+1}\le b_{i}\),使得 \(\sum\limits _{i=1}^{n} |a_i-b_i|\) 最小 .
- \(n\le 5\times 10^5\)
首先对于暴力转移,定义\(dp_{i,j}\)为转移到i点,权值为j的最小花费.
那么有转移方程 $dp_{i+1,j}= min(dp_{i,k})+|A_i-j| $ [k>=j]
然后分析\(dp_{i,j}\) 构成的函数,定义 \(f(x)=dp_i\) ,那么可以得到\(f(x)\)是一个下凸函数 [斜率单调不递减]
首先对于i=1的情况,图像是:
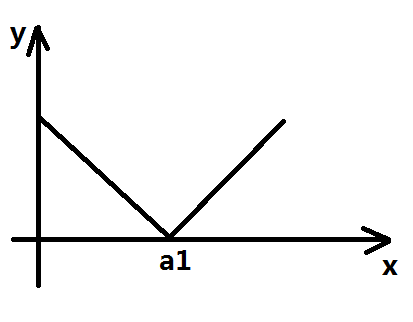
很显然是一个下凸函数
其中y表示花费,x表示b1的取值,a1表示原来第一个点的值
再观察上面给出的转移方程,发现对于一个j,用到的是大于等于自己的k对应的最小值
所以那段下降的函数是无用的
如果要转移到下一层的话,我们就只用管:
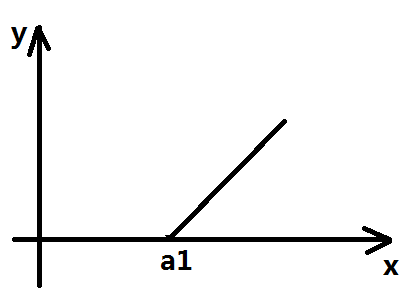
然后加入a2,但考虑a2构成的图像是和上面a1的图像相同的,然后再与修改后的转移图像相叠加,不难发现图像的斜率单调不减
由上面的推导可知:
加入一个数之后,图像会有所改变,并且我们不用管斜率小于等于0的部分函数
所以就始终维护一个斜率大于0且单调递增函数即可,并且答案就为那个下凹点
假设我们考虑 \(a_i\) ,那么 \(x< a_i\)的部分的斜率都要 -1,\(x> a_i\)的部分斜率都要 +1
加入第一个点后 \(f(x)\) 是一个斜率为1的递增函数
那么就放入\(a_1\),表示 \([a_1,\infty]\) 的局部函数斜率都为1
如果加入一个 \(a_2\)
若\(a_2\ge a_1\) ,那么 \([a_1,a_2]\) 的局部函数斜率变为0 ,\([a_2,\infty]\) 斜率变为2
若\(a_2<a1\) ,那么 \([a_2,a_1]\) 的局部函数斜率变成1,\([a_1,\infty]\) 的斜率变为2
对于第一种情况,可以看做 \([a1,\infty]\) $\to $ \([a1,a2],[a2,a2],[a2,\infty]\) 分别对应 0,1,2三种斜率
对于第二种情况,可以看做 \([a1,\infty]\) $\to $ \([a2,a1],[a1,\infty]\) 分别对应 1,2两种斜率
已知斜率小于等于0的函数部分是不要的
所以对于第一种情况,应该把\(a_1\)这个点给删掉,并加入两个\(a_2\)
而第二种情况,只需加入\(a_2\)即可
发现每次只需要调用最左边的点[即最小值],所以用堆维护即可
发现对于上述第一种情况,整个函数的下凹点改变了,假设原来凹点为\(f(a_1)=y_1\) ,\(,f(a_2)=y_1+k\times (a_2-a_1),k=1\) ,那么斜率改变后, 凹点位置转移到\(a_2\),对应 \(f(a_2)\)不变,所以答案增大\(a_2-a_1\)
RT
标签:mit 答案 修改 https math code limit rip 部分
原文地址:https://www.cnblogs.com/Zerokei/p/9866775.html