Bzoj 5195 [Usaco2018 Feb]Directory Traversal

标签：ESS   file   math   精通   点子   dir   编号   traversal   desc   

Descrtiption

奶牛Bessie令人惊讶地精通计算机。她在牛棚的电脑里用一组文件夹储存了她所有珍贵的文件，比如：

bessie/

  folder1/

?    file1

?    folder2/

?      file2

  folder3/

?    file3

  file4

只有一个“顶层”的文件夹，叫做bessie。

Bessie可以浏览任何一个她想要访问的文件夹。从一个给定的文件夹，每一个文件都可以通过一个“相对路径”被引用。

在一个相对路径中，符号“..”指的是上级目录。如果Bessie在folder2中，她可以按下列路径引用这四个文件：

../file1

file2

../../folder3/file3

../../file4

Bessie想要选择一个文件夹，使得从该文件夹出发，对所有文件的相对路径的长度之和最小。

\(N \leqslant 1e5\)

Solution

\(\,\,\,\,\,\,\,\,\,\,\,\)首先你得需要看懂题面（没看懂再看一次，我可不会解释）。典型的二次换根类题目。设\(len_i?\)为点i的名称长度，设\(f_i?\)为i到所有叶子点的长度之和，先考虑如何算出根的f值，再考虑如何用一个点更新其儿子，以此类推。
\(\,\,\,\,\,\,\,\,\,\,\,\)根的值很好求，因为只需要往下走。再考虑如何更新儿子。

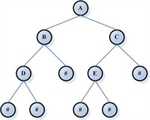
\(\,\,\,\,\,\,\,\,\,\,\,\) 用这个图打个比方，假设每个点的字符串长度就等于自身编号。我们先预处理出1号点到所有叶子点的总长度，再考虑更新7号点。对于所有在7号点子树内的叶子点，1号点必须先访问到7号点再下走访问各个点，所以7号点访问这些点的总长度=1号点访问的总长度-7号点子树内个数\(\times (len_7+1)\)，而除去7号点子树以外的叶子点只需让7号点先访问到一号点之后就和1号点的访问情况一样了，所以7号点访问这些点的总长度=1号点访问的总长度+(总点数-7号点子树内个数)\(\times 3\)。所以整合起来，7号点访问所有叶子点的总长度=1号点访问的总长度+总点数\(\times3-7\)号点子树内个数\(\times (4+len_7)\)。

Bzoj 5195 [Usaco2018 Feb]Directory Traversal

标签：ESS   file   math   精通   点子   dir   编号   traversal   desc   

原文地址：https://www.cnblogs.com/go-on/p/9867002.html