标签:val img nbsp opera info accept ++ width typename
题目传送门
题目大意
平面上有$n$个点,第$i$个点可以画一条平行于$y$轴且经过这个点的直线或者平行于$x$轴且经过这个点的直线或者什么都不做,问能够产生多少种本质不同的图案。
考虑每个点与它$x$坐标相同且$y$坐标比它大的第一个点连一条无向边,以及与它$y$坐标相同且$x$坐标第一个比它大的点连一条无向边。
显然,每个连通块和连通块之间互不影响,所以分别考虑每个连通块。
设当前连通块所有点的横坐标构成的集合为$X$,纵坐标构成的集合为$Y$。
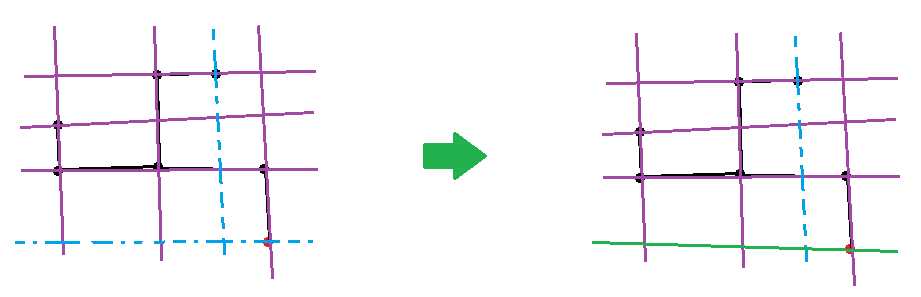
(其中蓝色虚线表示不存在的直线,紫色表示前$k - 1$个点选择的直线,绿色表示第$k$个点选择的直线,红点是第$k$个点)
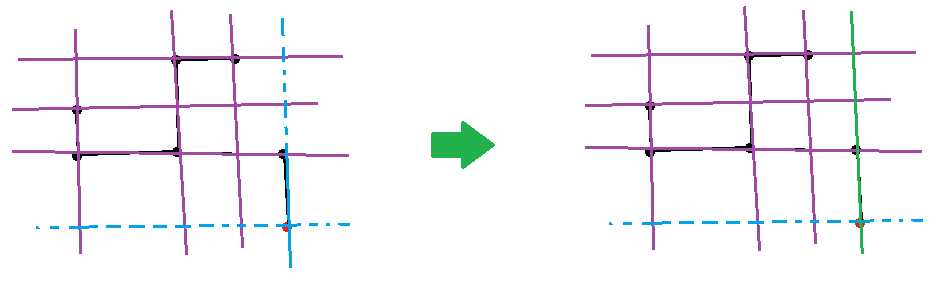
所以当一个连通块是树的时候方案数为$2^{|X| + |Y|} - 1$,否则是$2^{|X| + |Y|}$。
1 /** 2 * Codeforces 3 * Problem#870E 4 * Accepted 5 * Time: 93ms 6 * Memory: 9800k 7 */ 8 #include <algorithm> 9 #include <iostream> 10 #include <cstdlib> 11 #include <cstdio> 12 #include <set> 13 using namespace std; 14 typedef bool boolean; 15 16 template <typename T> 17 void pcopy(T* pst, const T* ped, T* pval) { 18 for ( ; pst != ped; *(pst++) = *(pval++)); 19 } 20 21 typedef class Point { 22 public: 23 int x, y, id; 24 25 Point(int x = 0, int y = 0, int id = 0):x(x), y(y), id(id) {} 26 }Point; 27 28 typedef class union_found { 29 public: 30 int n; 31 int *f; 32 int *dif; // |E| - |V| 33 34 union_found() { } 35 union_found(int n):n(n) { 36 f = new int[(n + 1)]; 37 dif = new int[(n + 1)]; 38 for (int i = 1; i <= n; i++) 39 f[i] = i, dif[i] = -1; 40 } 41 42 int find(int x) { 43 return (f[x] == x) ? (x) : (f[x] = find(f[x])); 44 } 45 46 void unit(int u, int v) { 47 int fu = find(u), fv = find(v); 48 if (fu == fv) { 49 dif[fu]++; 50 return; 51 } 52 dif[fu] += dif[fv] + 1; 53 f[fv] = fu; 54 } 55 56 int operator [] (int u) { 57 return find(u); 58 } 59 60 int operator () (int u) { 61 return dif[u]; 62 } 63 }union_found; 64 65 const int M = 1e9 + 7; 66 67 int add(int a, int b) { 68 return ((a += b) >= M) ? (a - M) : (a); 69 } 70 71 int mul(int a, int b) { 72 return a * 1ll * b % M; 73 } 74 75 int sub(int a, int b) { 76 return ((a -= b) < 0) ? (a + M) : (a); 77 } 78 79 int qpow(int a, int p) { 80 int pa = a, rt = 1; 81 for ( ; p; p >>= 1, pa = mul(pa, pa)) 82 if (p & 1) 83 rt = mul(rt, pa); 84 return rt; 85 } 86 87 int n; 88 Point* ps; 89 set<int> *sx, *sy; 90 union_found dsu; 91 92 inline void init() { 93 scanf("%d", &n); 94 ps = new Point[(n + 1)]; 95 for (int i = 1, x, y; i <= n; i++) { 96 scanf("%d%d", &x, &y); 97 ps[i] = Point(x, y, i); 98 } 99 } 100 101 inline void solve() { 102 dsu = union_found(n); 103 sort(ps + 1, ps + n + 1, [&] (const Point& a, const Point& b) { return (a.x ^ b.x) ? (a.x < b.x) : (a.y < b.y); }); 104 for (int i = 1, j, x; i <= n; i = j) { 105 for (x = ps[i].x, j = i + 1; j <= n && ps[j].x == x; j++); 106 for (int k = i; k < j; k++) 107 if (k + 1 < j) 108 dsu.unit(ps[k].id, ps[k + 1].id); 109 } 110 111 for (int i = 1; i <= n; i++) 112 swap(ps[i].x, ps[i].y); 113 sort(ps + 1, ps + n + 1, [&] (const Point& a, const Point& b) { return (a.x ^ b.x) ? (a.x < b.x) : (a.y < b.y); }); 114 for (int i = 1, j, x; i <= n; i = j) { 115 for (x = ps[i].x, j = i + 1; j <= n && ps[j].x == x; j++); 116 for (int k = i; k < j; k++) 117 if (k + 1 < j) 118 dsu.unit(ps[k].id, ps[k + 1].id); 119 } 120 121 sx = new set<int>[(n + 1)]; 122 sy = new set<int>[(n + 1)]; 123 for (int i = 1, p; i <= n; i++) { 124 p = ps[i].id; 125 sx[dsu[p]].insert(ps[i].x); 126 sy[dsu[p]].insert(ps[i].y); 127 } 128 int res = 1; 129 for (int i = 1; i <= n; i++) { 130 if (dsu[i] == i) 131 res = mul(res, sub(qpow(2, sx[i].size() + sy[i].size()), (dsu(i) < 0))); 132 } 133 printf("%d\n", res); 134 } 135 136 int main() { 137 init(); 138 solve(); 139 return 0; 140 }
Codeforces 870E Points, Lines and Ready-made Titles
标签:val img nbsp opera info accept ++ width typename
原文地址:https://www.cnblogs.com/yyf0309/p/9873974.html