标签:相关 eset oid mes http bubuko ... 技术分享 hit
7.1 过拟合问题 The Problem of Overfitting
7.2 代价函数 Cost Function
7.3 正则化线性回归 Regularized Linear Regression
7.4 正则化的逻辑回归模型 Regularized Logistic Regression
参考视频: 7 - 1 - The Problem of Overfitting (10 min).mkv
回归问题:
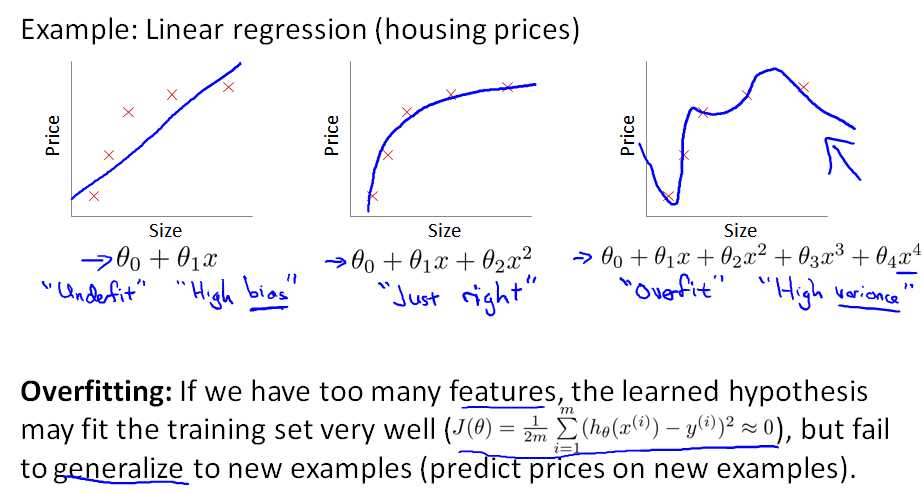
分类问题:
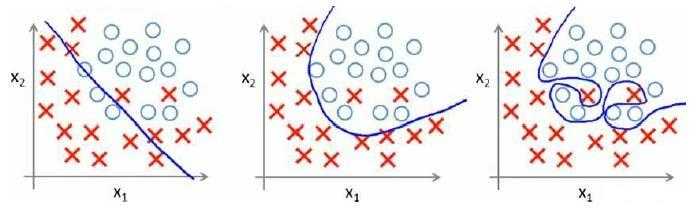
解决方法:
1) 减少 feature 的个数:
2) 正则化
参考视频: 7 - 2 - Cost Function (10 min).mkv
如果线性回归出现过拟合,曲线方程如下:
![]()
如果想消除高次幂项的影响,可以修改代价函数 ,在某些参数上设置一些惩罚,一定程度上减小这些参数的影响:
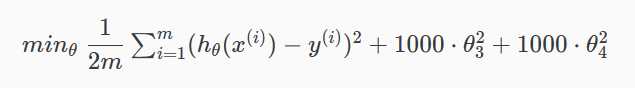
要使代价函数趋于0,则需降低θ3和θ4的值,因为二次项≥0,所以令它们为0时代价函数最小,降低了他们在hypothesis function的影响,从而减少了过拟合。这就是正则化的思想。
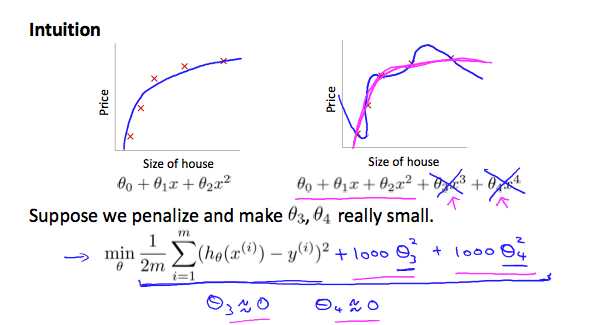
实际使用中,因为不知道具体应该惩罚那些参数。所以给所有参数都加一个系数 λ:
![]()
λ or lambda 叫做 regularization parameter,加号后面这一项叫做 regularization term。
1)如果 λ = 0或者特别小,起不到作用,仍然过拟合。
1)如果 λ 选的太大,所有参数都遭到惩罚。最后假设方程可能变成 h(x) = θ0,导致欠拟合 underfitting。
参考视频: 7 - 3 - Regularized Linear Regression (11 min).mkv
正则化线性回归的代价函数为:
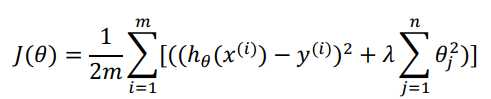
因为正则化不涉及到 θ0,梯度下降算法如下:

对上面的算法第二个式子调整可得
![]() ( j ∈ 1,2 ... n)
( j ∈ 1,2 ... n)
正则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令 θ减少了一个额外的值。
如果使用正规方程 Normal Equation方法,引入一个 (n+1)×(n+1)维的方阵L,正则化如下:
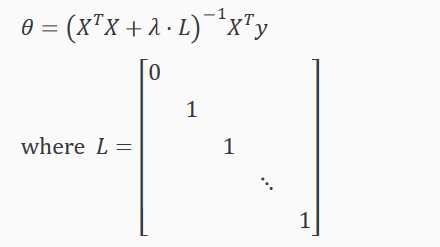
注:当 m < n 时,XTX 不可逆non-invertible。但是当加上 λ⋅L,XTX+ λ⋅L 变为可逆矩阵 invertible。
参考视频: 7 - 4 - Regularized Logistic Regression (9 min).mkv
逻辑回归的代价函数为:
![]()
加上正则项之后:
![]()
注:这个代价函数看上去同正则化线性回归的式子一样,但是两个 ? 不同,所以有很大差别。
θ0不参与任何正则化
效果(蓝色线是正则化之前,粉色线是正则化之后):
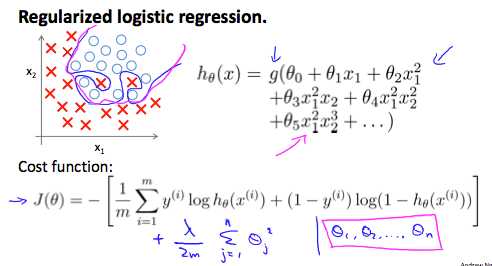
仍然可以用 fminuc 函数来求解代价函数最小化的参数 ,但我们实现的 costFunction 函数中进行了正则化:

python代码
1 import numpy as np
2 def costReg(theta, X, y, learningRate):
3 theta = np.matrix(theta)
4 X = np.matrix(X)
5 y = np.matrix(y)
6 first = np.multiply(-y, np.log(sigmoid(X*theta.T)))
7 second = np.multiply((1 - y), np.log(1 - sigmoid(X*theta.T)))
8 reg = (learningRate / (2 * len(X))* np.sum(np.power(theta[:,1:the
9 ta.shape[1]],2))
10 return np.sum(first - second) / (len(X)) + reg
decision boundary 决策边界
loophole 漏洞
nonlinear 非线性
penalize the parameter 惩罚参数
regularization term 正则项
regularization parameter 正则化参数
wiggly/curvy 摆动的 弯曲的
optimization objective 优化目标
lamda 即 λ
shrinking 收缩
magnitude 量级,重要性
【原】Andrew Ng斯坦福机器学习(7)——Lecture 7
标签:相关 eset oid mes http bubuko ... 技术分享 hit
原文地址:https://www.cnblogs.com/maxiaodoubao/p/9880971.html