标签:png 操作 pre nbsp namespace 互连 temp 时间 printf
画画图可以发现,只要是两个点之间没有相互连边,那么就必须将这两个人安排到同一个办公楼内,如图所示:
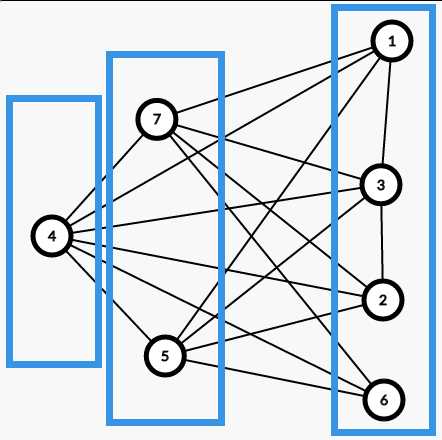
那,我们可以建立补图,就是先建一张完全图,然后把题目中给出的边都删掉,这就是一张补图,显然补图中相互连边的点就放在同一栋办公楼内。
我们可以用并查集来完成,但是数据范围显然不允许用这样的方法,建图的复杂度是 $N^2$ 的。所以考虑另一种方法:
将原图建立好,在原图中,从一个点开始,把这个点所能够直接到达的点标记出来,这些点是不可以放在一起的。然后将这些点删除。
之后对每一个点都进行这样的操作,那么之后要删除的点都要满足既没有被删除也没有被标记。这样做下来的复杂度还是 $N^2$ 的。再来想想如何优化,我们如果在删点的时候,不去枚举那些已经被删除的点。那所有的删点的操作总时间复杂度是 $M$ 的,因为每个边都要只遍历一次。如何优化?链表啊。。。
#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #include <queue> using namespace std; template <typename T> inline void read(T &x) { x = 0; T f = 1; char c = getchar(); while (c < ‘0‘ || c > ‘9‘) {if(c == ‘-‘) f = -1; c = getchar();} while (c <= ‘9‘ && c >= ‘0‘) {x = x*10 + c-‘0‘; c = getchar();} x *= f; } const int maxn = 4e6+3; int n, m, head[maxn], cnt, ans, pre[maxn], sur[maxn], num[maxn]; bool vis[maxn], del[maxn]; struct edge {int nxt, to;}ed[maxn]; inline void addedge(int x, int y) { ed[++cnt].nxt = head[x], head[x] = cnt, ed[cnt].to = y; } inline void DEL(int x) { sur[pre[x]] = sur[x]; pre[sur[x]] = pre[x]; del[x] = 1; } inline void BFS(int u) { queue<int> Q; Q.push(u), vis[u] = 1; while (!Q.empty()) { int now = Q.front(); Q.pop(); num[ans] ++; for(int i=head[now]; i; i=ed[i].nxt) vis[ed[i].to] = 1; for(int i=sur[0]; i<=n; i=sur[i]) if(!vis[i] && !del[i]) Q.push(i), DEL(i); for(int i=head[now]; i; i=ed[i].nxt) vis[ed[i].to] = 0; } } int main() { read(n), read(m); int u, v; for(int i=1; i<=m; i++) { read(u), read(v); addedge(u, v), addedge(v, u); } for(int i=0; i<=n; i++) pre[i] = i-1, sur[i] = i+1; for(int i=1; i<=n; i++) if(!del[i]) del[i] = 1, ans ++, BFS(i), DEL(i); sort(num+1, num+1+ans); printf("%d\n", ans); for(int i=1; i<=ans; i++) printf("%d ", num[i]); return 0; }
标签:png 操作 pre nbsp namespace 互连 temp 时间 printf
原文地址:https://www.cnblogs.com/bljfy/p/9880973.html