openGL坐标系

标签：渲染   固定   直接   device   模型   screen   mod   坐标系统   来讲   

从我们构造模型的局部坐标系（Local/Object Space）经过一系列的处理最终渲染到屏幕坐标系(Screen Space)下,这个过程有6种坐标系。

一、世界坐标系（World Coordinates）

学名：右手笛卡尔坐标系统。

在OpenGL中，世界坐标系是以屏幕中心为原点(0, 0, 0)，且是始终不变的。x轴正方向为屏幕从左向右，y轴正方向为屏幕从下向上，z轴正方向为屏幕从里向外。长度单位这样来定：窗口范围按此单位恰好是(-1,-1)到(1,1)，即屏幕左下角坐标为（-1，-1），右上角 坐标为（1,1）。

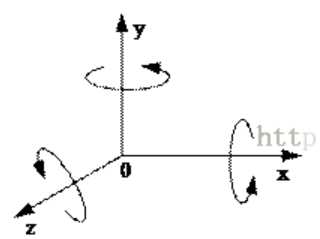
进行旋转操作时需要指定的角度θ的方向则由右手法则来决定，即右手握拳，大拇指直向某个坐标轴的正方向，那么其余四指指向的方向即为该坐标轴上的θ角的正方向（即θ角增加的方向），在上图中用圆弧形箭头标出。

坐标变换矩阵栈：

用来存储一系列的变换矩阵，栈顶就是当前坐标的变换矩阵，进入OpenGL管道的每个坐标(齐次坐标)都会先乘上这个矩阵，结果才是对应点在场景中的世界坐标。OpenGL中的坐标变换都是通过矩阵运算完成的。 
如图： 

对象坐标系（乘以模型视图矩阵）--->眼睛坐标系（乘以投影矩阵）--->裁剪坐标系（除以w）--->标准设备坐标系--->设备坐标系

二、对象/模型/局部/绘图坐标系(object coordinate)

这是对象在被应用任何变换之前的初始位置和方向所在的坐标系，也就是当前绘图坐标系。该坐标系不是固定的，且仅对该对象适用。在默认情况下，该坐标系与世界坐标系重合。这里能用到的函数有glTranslatef()，glScalef(), glRotatef()，当用这些函数对当前绘图坐标系进行平移、伸缩、旋转变换之后， 世界坐标系和当前绘图坐标系不再重合。改变以后，再用glVertex3f()等绘图函数绘图时，都是在当前绘图坐标系进行绘图，所有的函数参数也都是相对当前绘图坐标系来讲的。如图则是对物体进行变换后，对象坐标系与世界坐标系的相对位置。

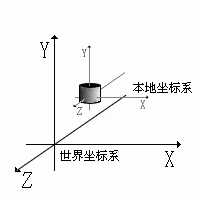
三、眼/照相机坐标系（eye coordinate）

模型变换：对象坐标系-->世界坐标系

视图变换：世界坐标系-->眼睛坐标系

GL_MODELVIEW矩阵是模型变换和试图变换矩阵的组合（view*model）,因为没有单独的模型变换和视图变化，所以使用GL_MODELVIEW矩阵可以使对象直接从对象坐标系转换到眼睛坐标系。

为什么要转换到眼睛坐标系？

因为我们的观察位置没定，如果我们的眼睛（照相机）的位置不同，那么观察物体的角度则不同，看到的样子也不同，所有要有这一步，把场景与我们的观察位置对应起来。

默认情况下，眼睛坐标系与世界坐标系也是重合的。使用gluLookAt()则可以指定眼睛（相机）的位置和眼睛看的方向。该函数的原型如下：

1 void gluLookAt(GLdouble eyex, GLdouble eyey, GLdouble eyez, 
2                         GLdouble centerx, GLdouble centery, GLdouble centerz,
3                         GLdouble upx, GLdouble upy, GLdouble upz);

函数参数中,点(eyex, eyey, eyez)代表眼睛所在位置；
点(centerx, centery,centerz)代表眼睛看向的位置；
向量(upx, upy, upz)代表视线向上方向,其中视点和物体的连线与视线向上方向要保持。

注：

四、裁剪坐标系（clip coordinate）

眼坐标到裁剪坐标是通过投影完成的。眼坐标通过乘以GL_PROJECTION矩阵变成了裁剪坐标。

投影分为透视投影（perspective projection）和正交投影（orthographic projection）

1>透视投影

类似日常生活看到的场景，远大近小。透视投影函数有两个：gluPerspective()和glFrustum()

1 void glFrustum(GLdouble left, GLdouble right,
2 　　　　　 GLdouble bottom, GLdouble top, 
3 　　　　　 GLdouble near, GLdouble far)

1 void gluPerspective(GLdouble fovy,  GLdouble aspect,
2 　　　　　　　   GLdouble near, GLdouble far) 

far, near是指近裁剪面，远剪裁面离视点的距离(>0),fovy视角，aspect = w/h

2>正投影

1 void glOrtho(GLdouble left, GLdouble right,
2 　　　　       GLdouble bottom, GLdouble top, 
3 　　　　       GLdouble near, GLdouble far);

把物体直接映射到屏幕上，不影响它的相对大小。也就是图像反映物体的实际大小。

五、归一化设备坐标系(normalized device coordinate)

在裁剪坐标系下通过除以w分量得到，这个操作称为透视除法。得到的坐标值均为[-1,1]

六、屏幕坐标（screen coordinate）

屏幕坐标的x轴向右为正，y轴向下为正，坐标原点位于窗口的左上角。是归一化设备坐标系通过视口变换得到（viewport）

几何变换

OpenGL中可以使用的几何变换有平移、旋转、缩放三种。

glTranslatef(x, y, z);

该函数可以实现平移变换，x、y、z为各坐标轴上的平移量。

glRotatef(θ, x, y, z);

该函数实现旋转变换。θ为旋转角度，x、y、z为旋转轴。旋转方向由右手法则决定（参见第一节“坐标系”）。

glScalef(x, y, z);

该函数实现缩放变换。x、y、z为各轴方向的扩大量。若为负值，则沿着坐标轴的反方向进行缩放。

openGL坐标系

标签：渲染   固定   直接   device   模型   screen   mod   坐标系统   来讲   

原文地址：https://www.cnblogs.com/keguniang/p/9886605.html