标签:rac splay width display mit info 开始 ali float
学习曲线
“训练误差”和“交叉验证误差”如下
\[\begin{array}{l}
{J_{train}}\left( \theta \right) = \frac{1}{{2{m_{train}}}}\sum\limits_{i = 1}^{{m_{train}}} {{{\left( {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right)}^2}} \\
{J_{CV}}\left( \theta \right) = \frac{1}{{2{m_{CV}}}}\sum\limits_{i = 1}^{{m_{CV}}} {{{\left( {{h_\theta }\left( {x_{CV}^{\left( i \right)}} \right) - y_{CV}^{\left( i \right)}} \right)}^2}}
\end{array}\]
对于
\[{h_\theta }\left( x \right) = {\theta _0} + {\theta _1}x + {\theta _2}{x^2}\]
当训练样本从1增加到6时,会出现和下图类似的情况
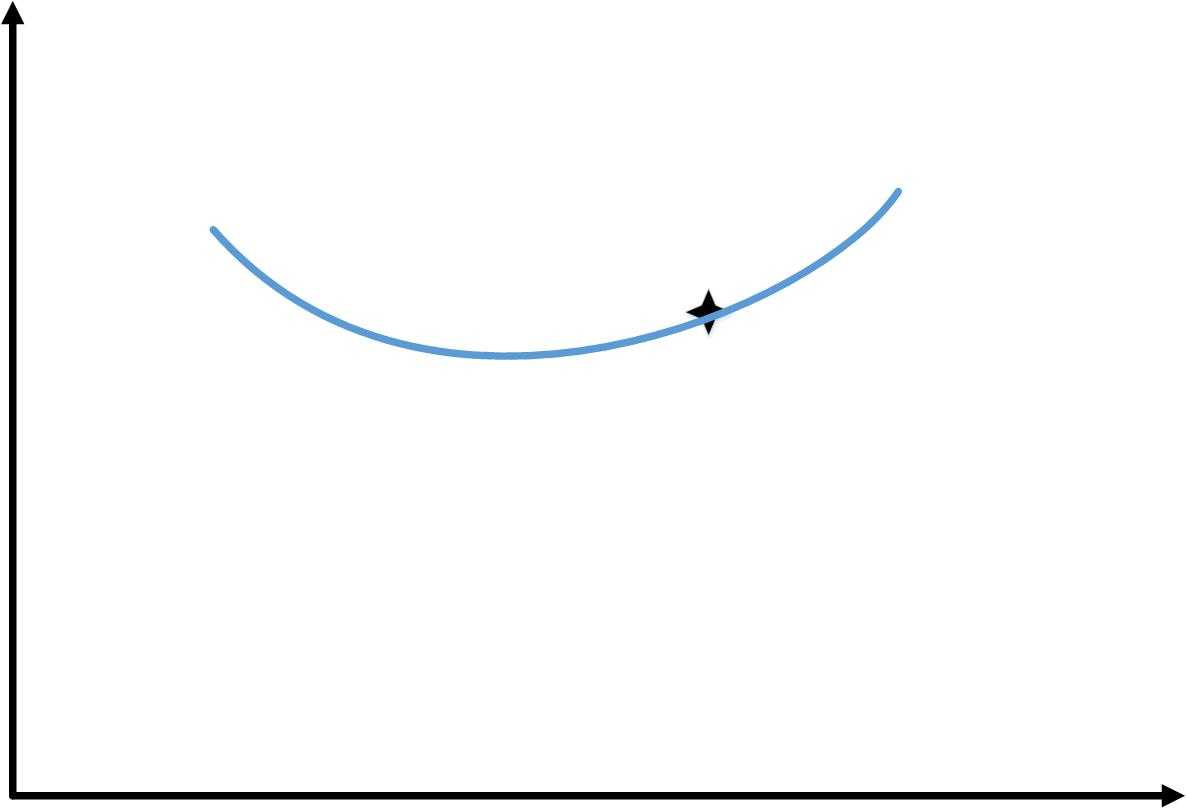
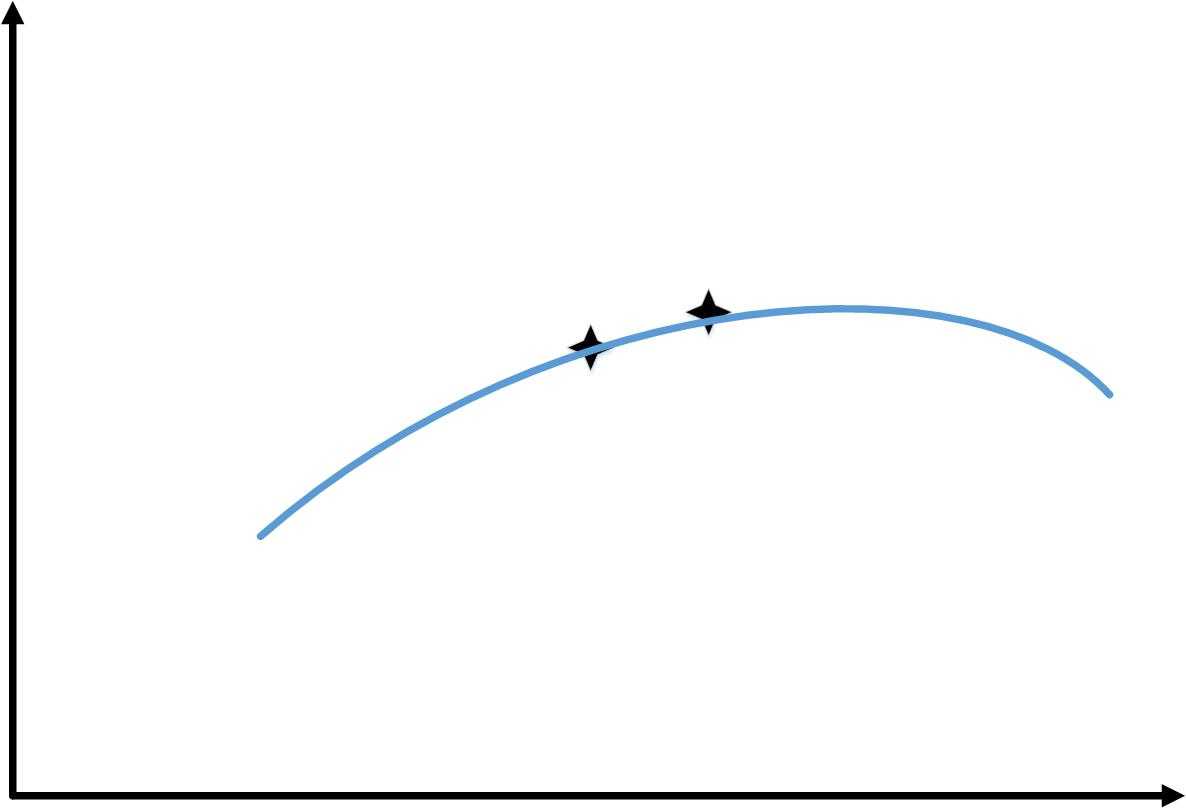
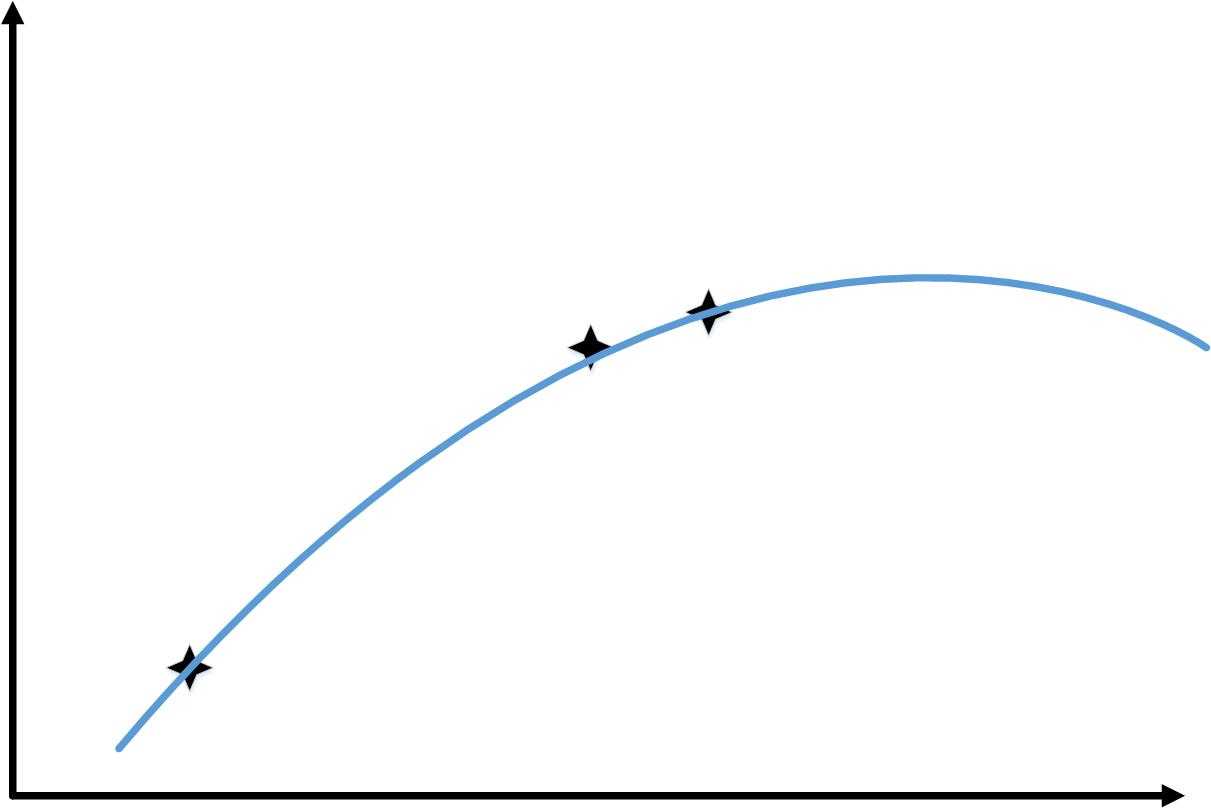
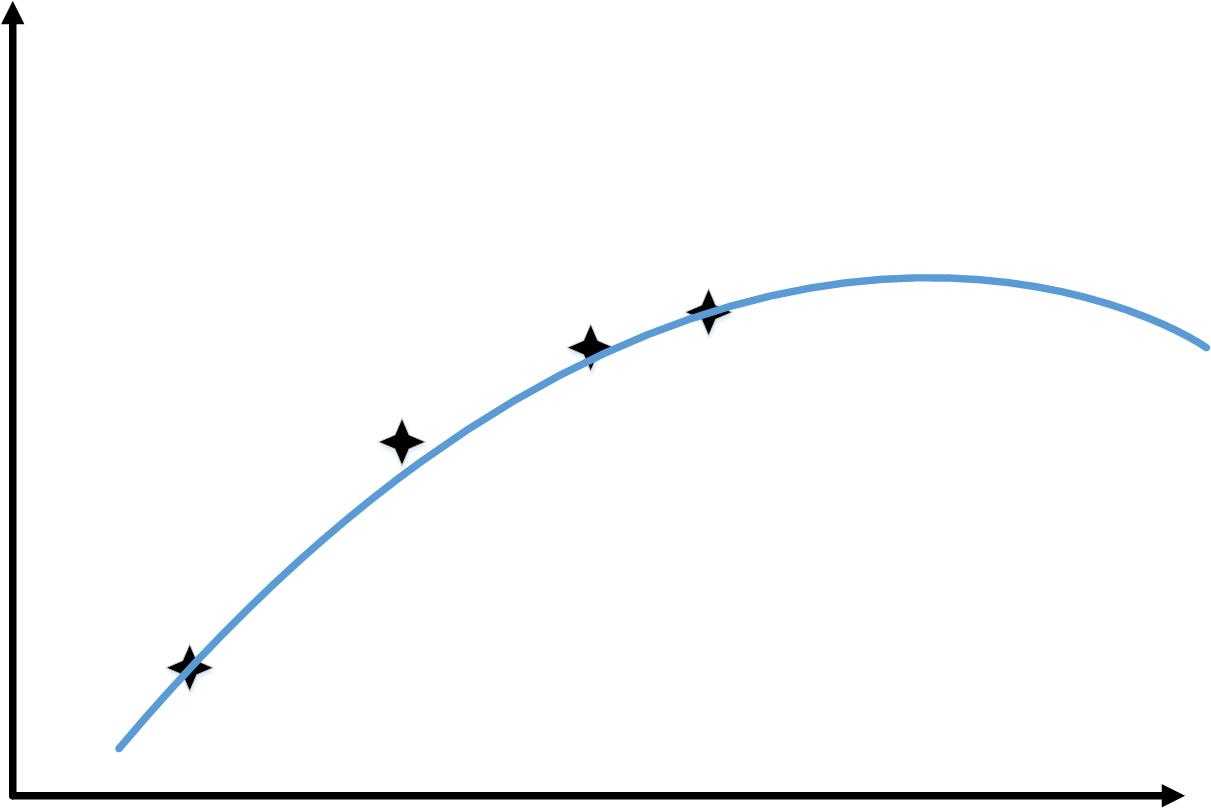
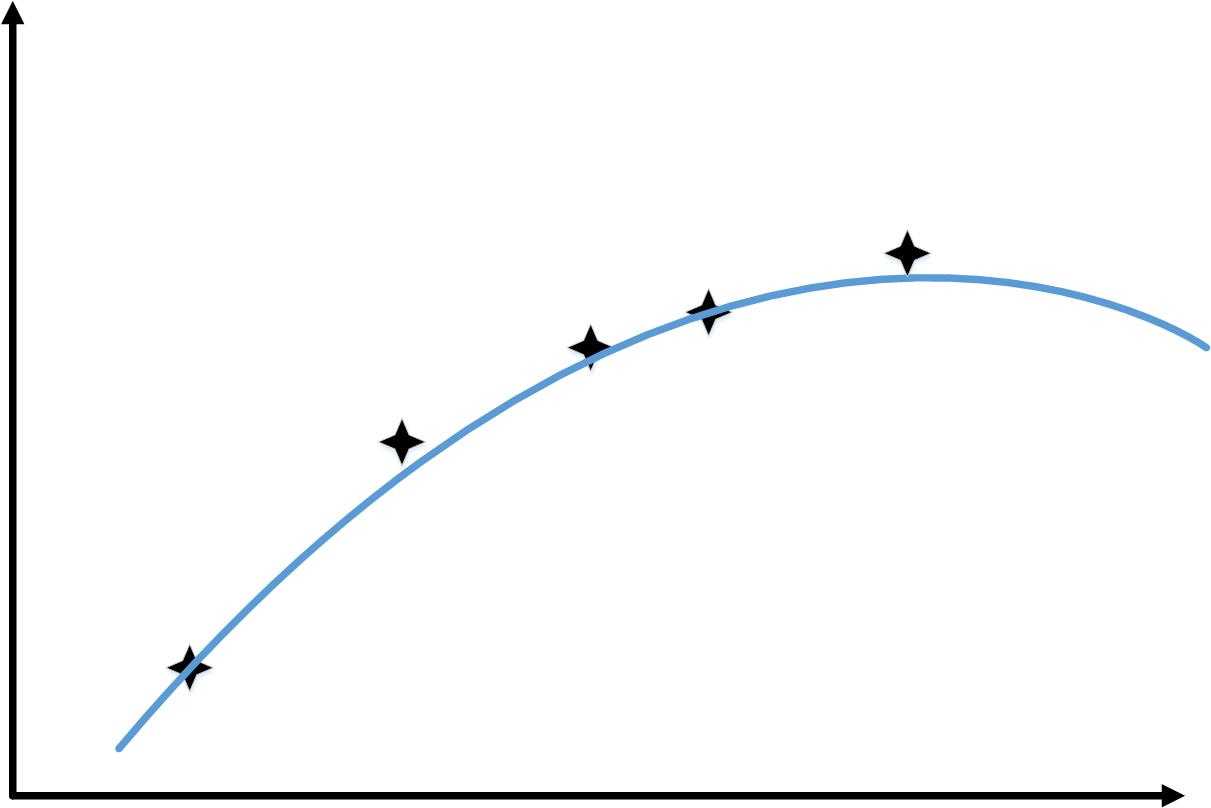
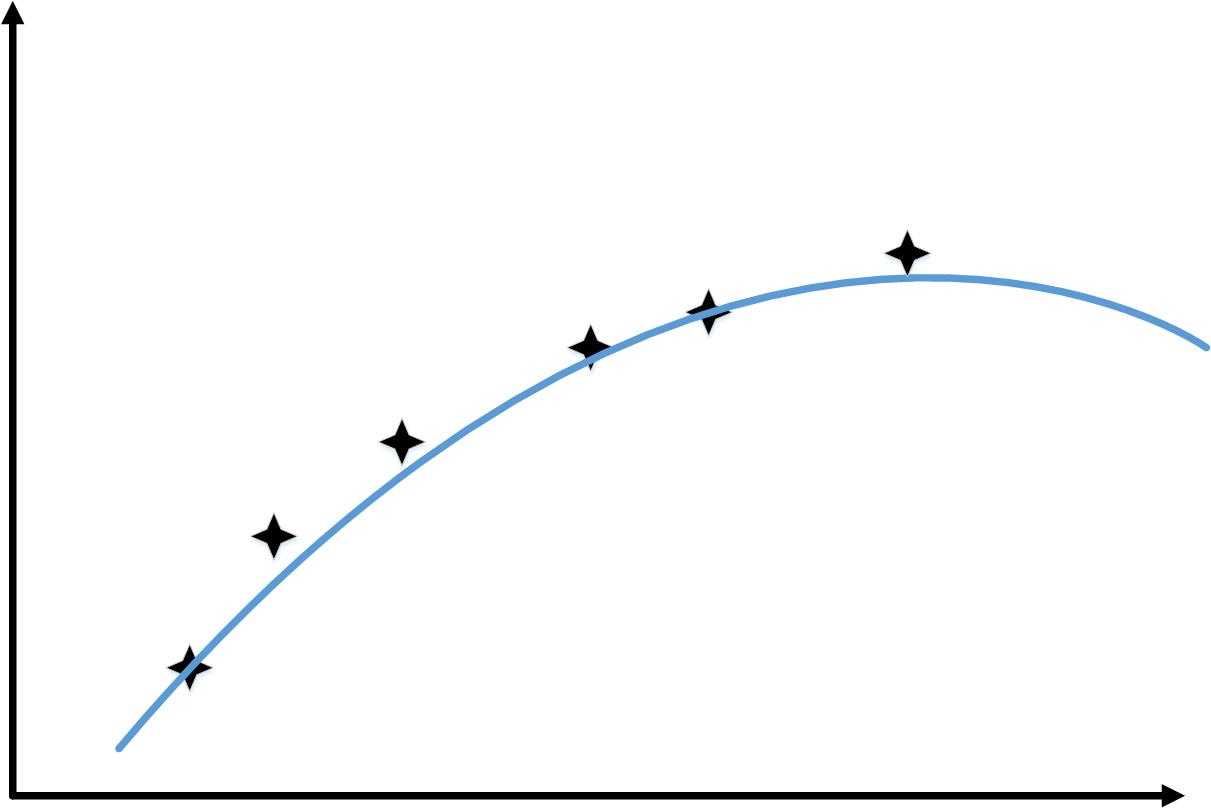
这样,随着训练样本的增加,“训练误差”和“交叉验证你误差”的变化如下图
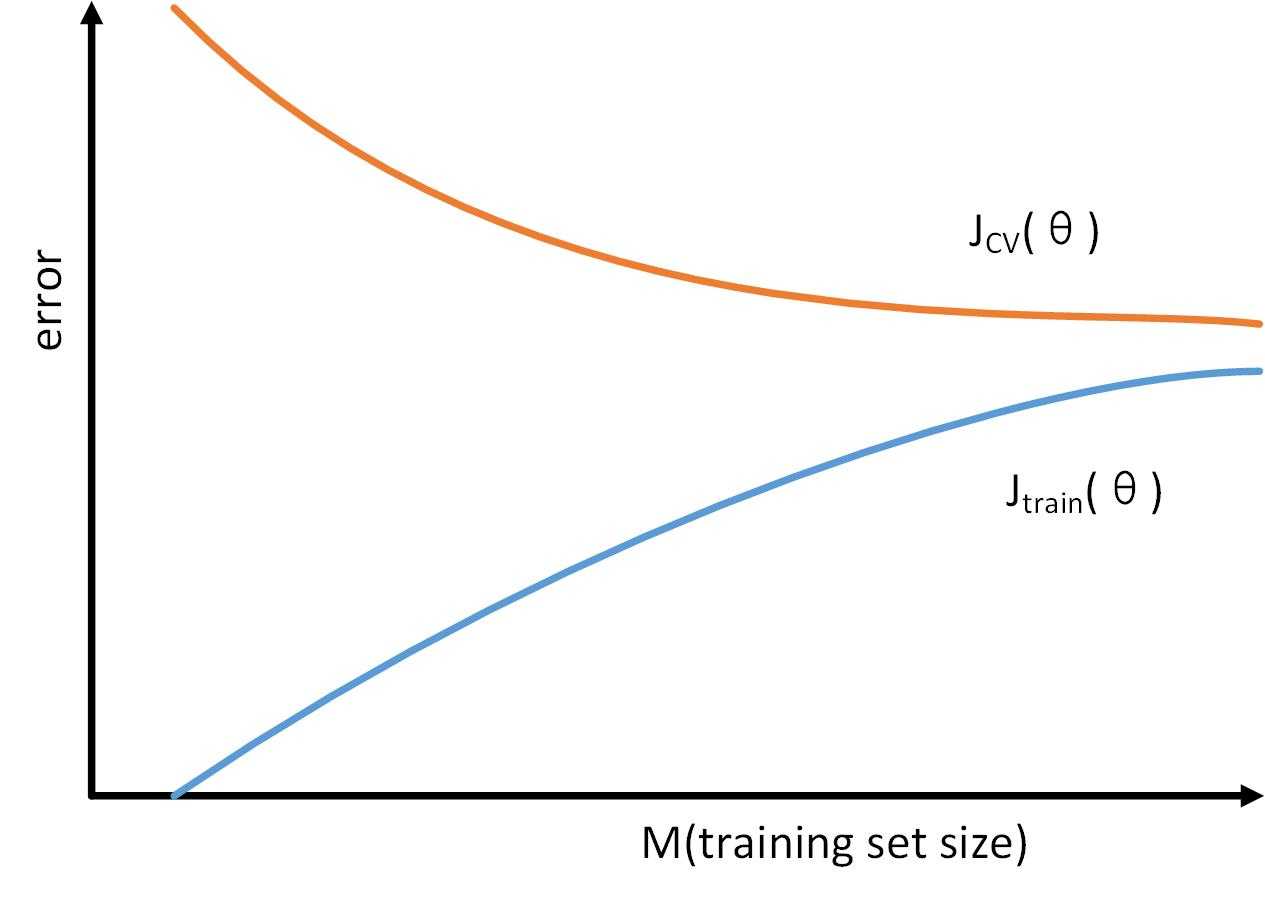
对于“High bias”情况
\[{h_\theta }\left( x \right) = {\theta _0} + {\theta _1}x\]
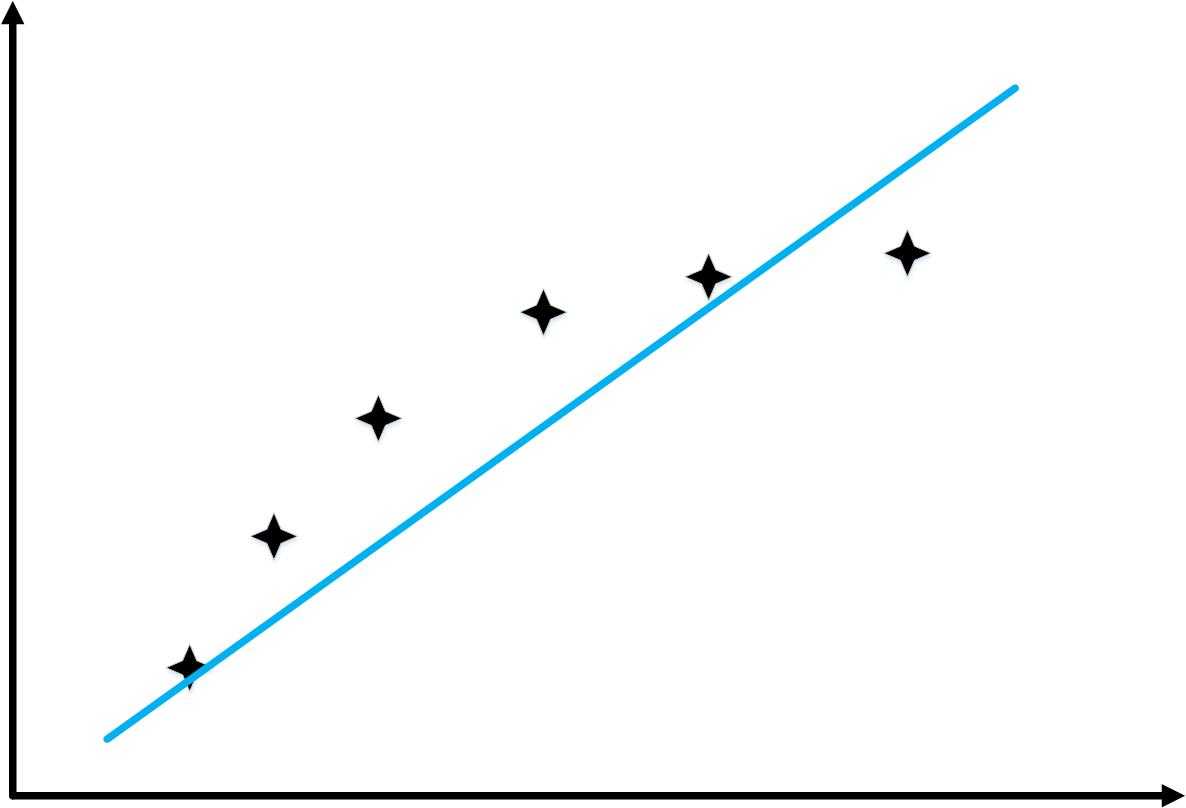
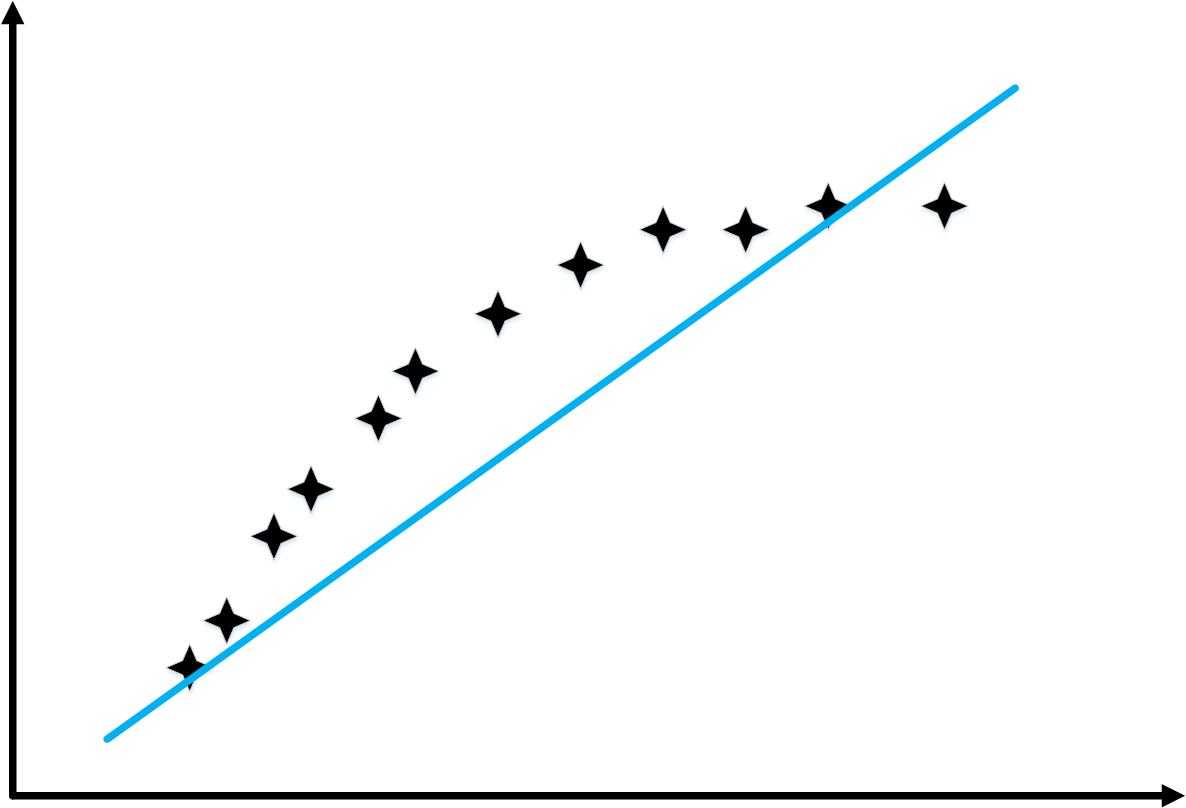
随着训练样本的增加,“训练误差”和“交叉验证你误差”的变化如下图
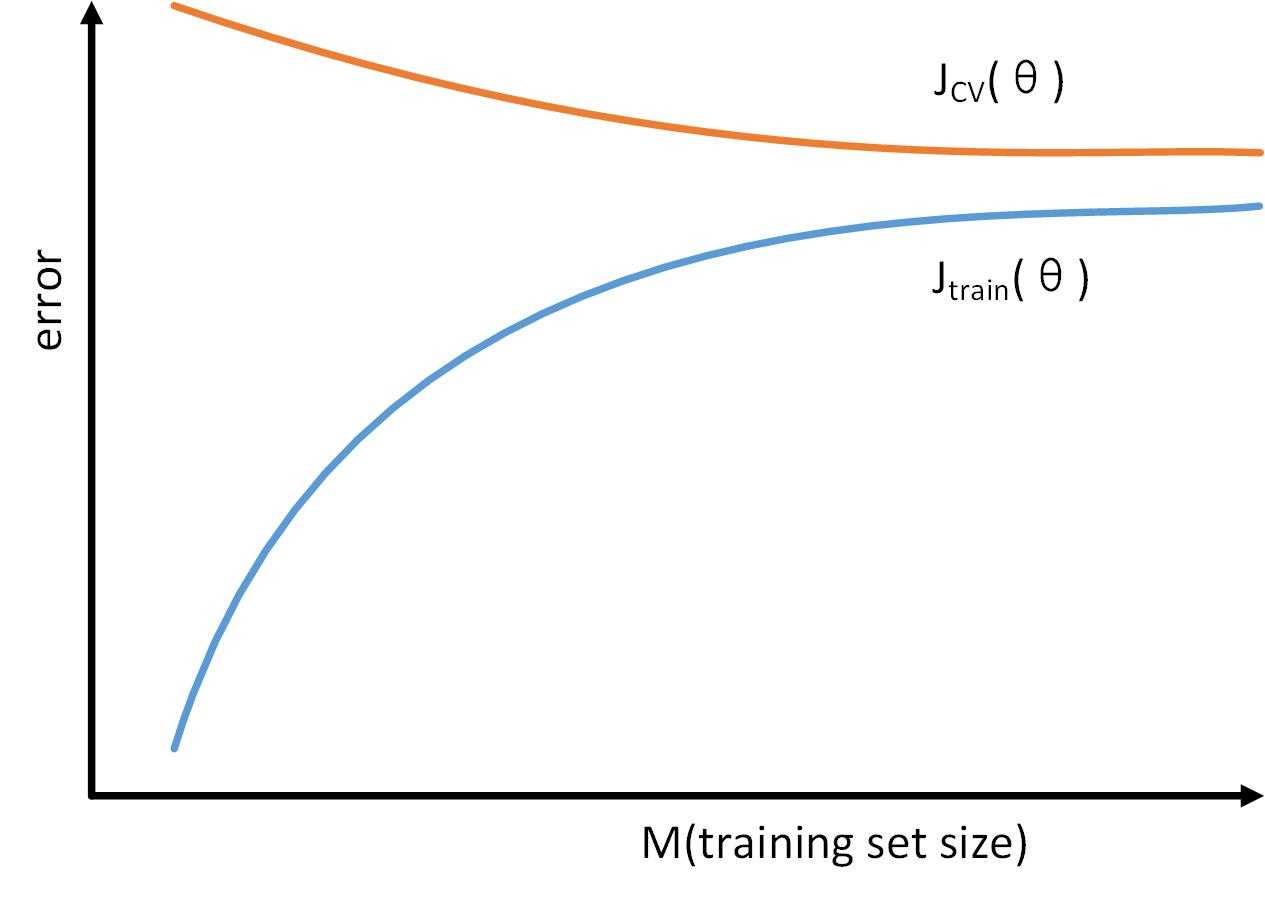
可以看到,两者都很大。因此,如果是“High bias”的情况,增加训练样本作用不大。
对于“High variance”情况
\[{h_\theta }\left( x \right) = {\theta _0} + {\theta _1}x + ... + {\theta _{100}}{x^{100}}\]
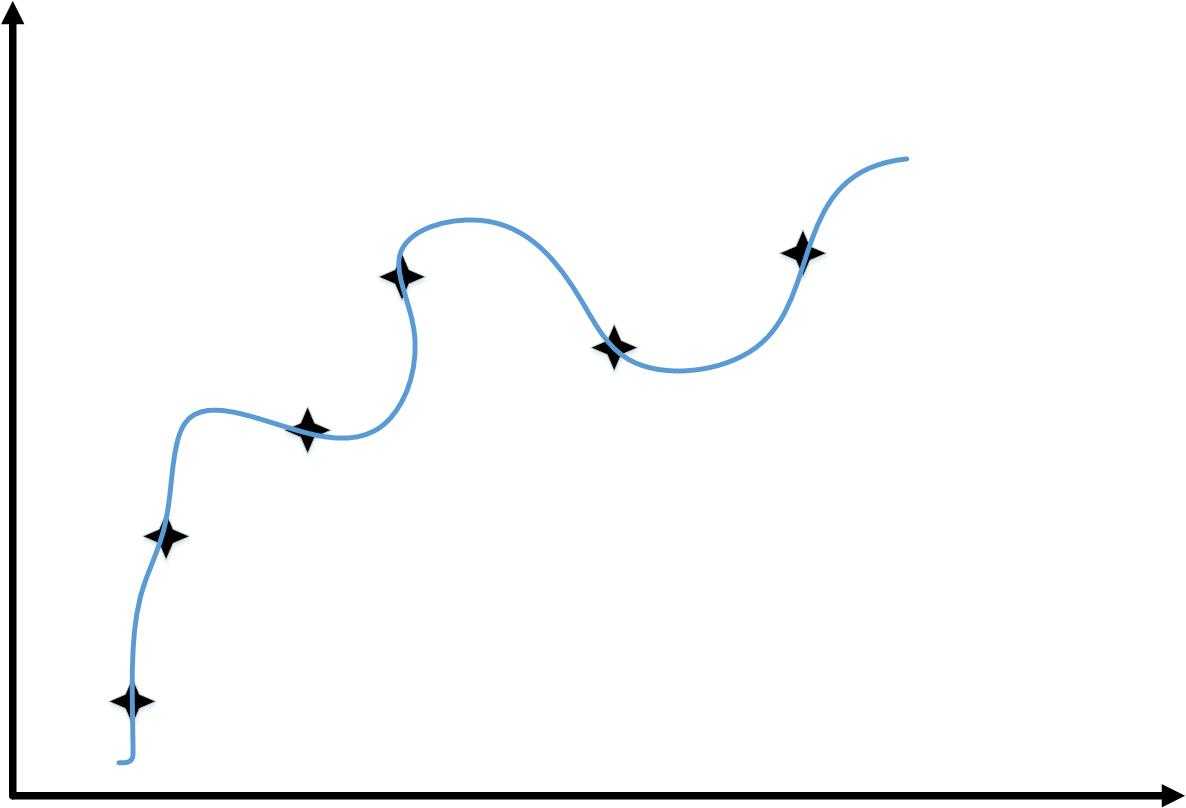

随着样本数量的增加,“训练误差”和“交叉验证你误差”的变化如下图
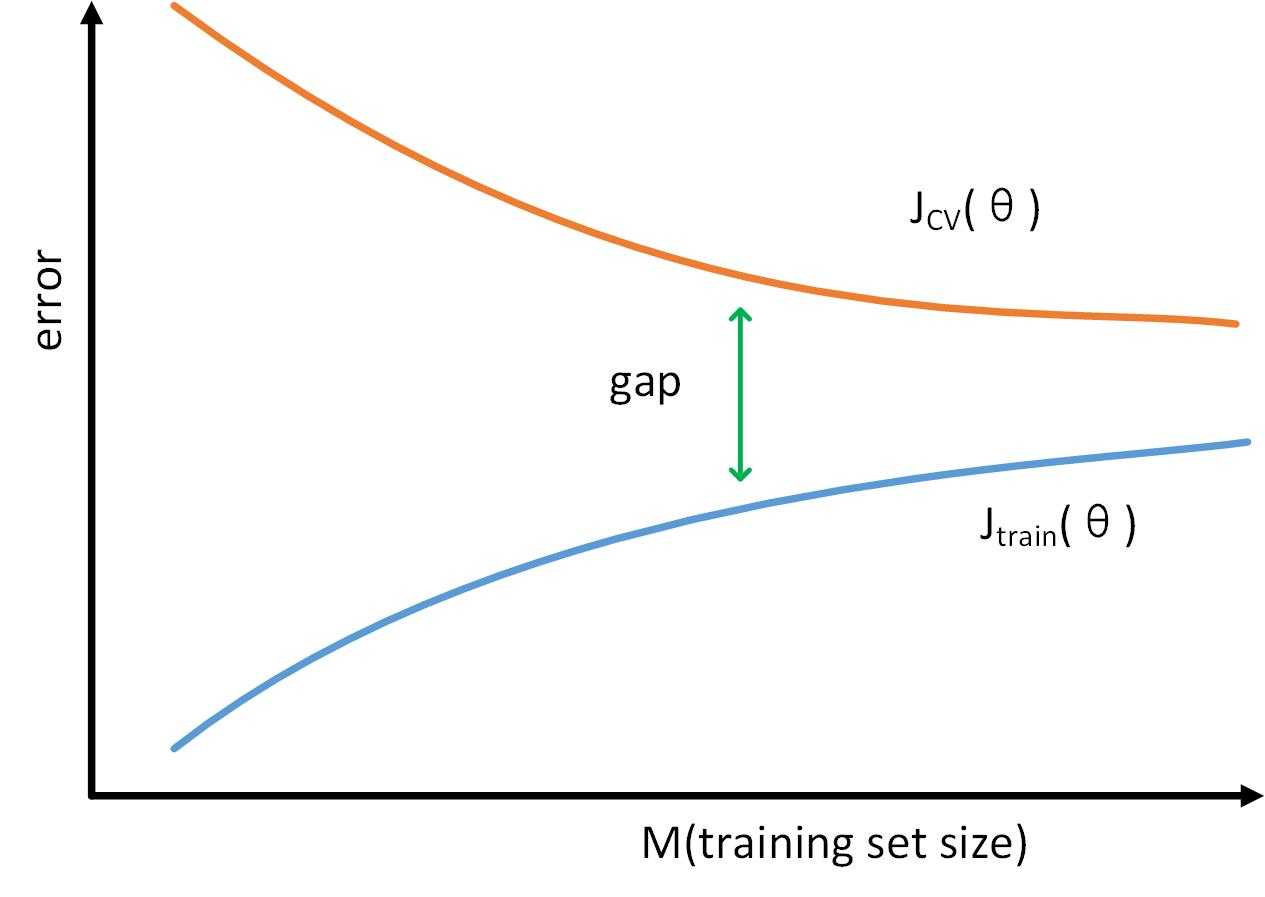
由于是“High variance”情况,刚开始模型对少量训练样本的适应度高,“训练误差”较小,“交叉验证误差”较大。随着训练样本的增加,两个误差之间存在明显的“gap”,如果继续加大样本,“交叉验证误差”可能会逐渐降低。因此,对于“High variance”情况,增加训练样本可能会有帮助。
标签:rac splay width display mit info 开始 ali float
原文地址:https://www.cnblogs.com/qkloveslife/p/9887115.html