深入浅出看递归

标签：rom   ring   很多   inf   回文串   com   基础   col   span   

本来以为可以不用写这一篇文章的,奈何最近学弟学妹反映深度优先搜索听不懂,原因可能与递归有关?那就写一篇文章,以我微薄的水平尝试阐述一下递归的伟大思想.

首先看定义: 程序调用自身的编程技巧称为递归

然后让我们用一个图,抽象出程序执行过程可能出现的情况:

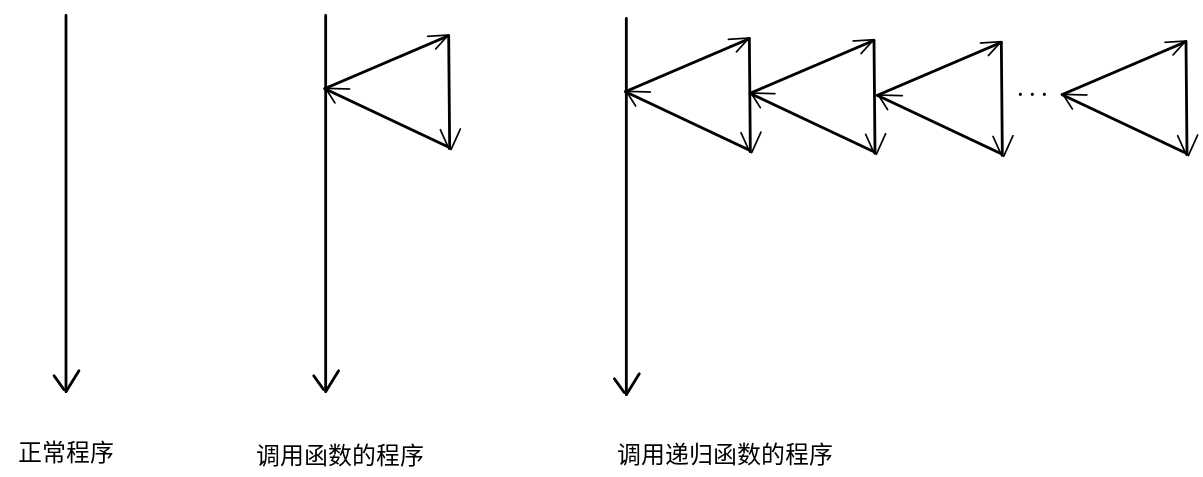
其中上图的箭头表示程序语句执行的方向,我们知道正常程序,都是从上到下线性执行的,如上图,而调用函数的程序,它会跳转到另一个函数中去执行,结束后会回到断点处继续执行原程序,总体上还是线性的.那么递归呢? --递归也只是调用函数,只不过是在一个函数内部调用该函数自身,进入一个新的"自我执行"的阶段,而且在这个阶段里面又会遇见一条调用自身的语句,从而开始新一轮的"轮回".但如果设计得当,我们让函数在适当的时候停止调用自身,而是返回,那么这些函数也一定会在一个点不满足递归的条件,从而层层返回,直到最后一个递归函数被返回,进入原程序继续执行到结束的过程

所以我们可以归纳一下递归的几个要素:

1.函数内部由自我调用语句;

2.必须存在递归出口;

如此,我们可以写一个基础的递归通式:

void fun()
{
    if(递归出口 == true)
        return;
    fun();
}

上面的代码虽然简单,却反映了递归的两个性质,并非所有的递归函数都是这样写,但是所有的递归函数必定满足上面的性质.

我们来看几个简单的例子:

1.递归求斐波那契数列

int fib(int x)
{
    if(x == 1 || x == 2)    return 1;
    return fib(x-1) + fib(x-2);
}

2.递归求阶乘

int factorial(int x)
{
    if(x == 0 || x == 1)  return 1;
    return x*factorial(x-1);
}

以上都是我们熟悉的递归,因为斐波那契数列和阶乘在数学上都是递归定义的,所以递归实现非常方便.那为什么递归出口如此小的一个返回值,到最后能计算出非常大的数的阶乘或者斐波那契数列的第很多位呢?原因在于递归的第二个返回值,即if落空后执行的语句,这条语句将反复执行很多次才能执行到if条件满足,此时层层返回,虽然一开始的返回值很小,但是返回的路径很深,导致结果就像滚雪球一样慢慢积累,到最后一个返回结束后,结果就很大了.

下面我们再仿照上面的形式,写一些我们不太熟悉的递归函数:

1.递归判断回文串

bool parlindrome(string str,int l,int r)
{
    if(l == r || r-l == 1)  return 1;
    if(str[l] != str[r])    return 0;
    return parlindrome(str,l+1,r-1);
}

深入浅出看递归

标签：rom   ring   很多   inf   回文串   com   基础   col   span   

原文地址：https://www.cnblogs.com/AAMahone/p/9892398.html