标签:老师 -- 对象 最好 两种 因此 过程 private 迭代

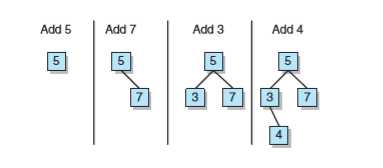
列表的一些常见操作

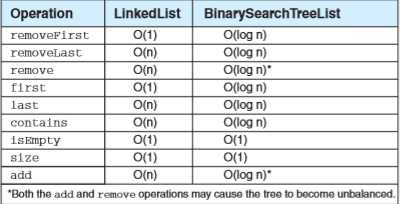
有序列表的特有操作

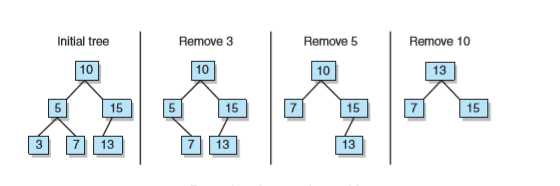
如果二叉查找树不平衡,其效率可能比线性结构的还要低。例如蜕化树看起来更像一个链表,事实上它的效率比链表的还低,因为每个结点附带有额外的开销。
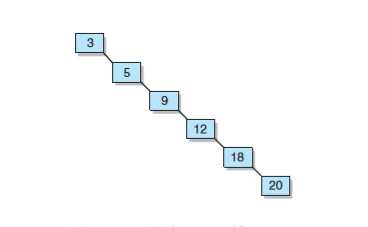
我们的目标是保持树的最大路径长度为(或接近)log2n。
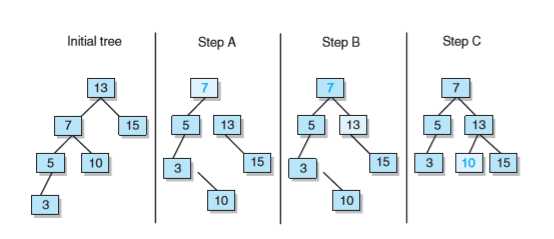
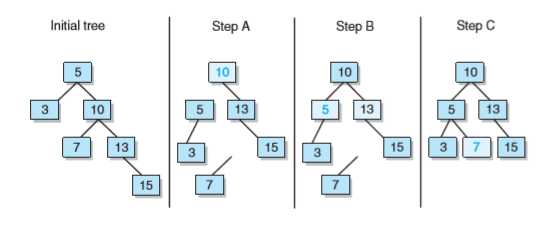
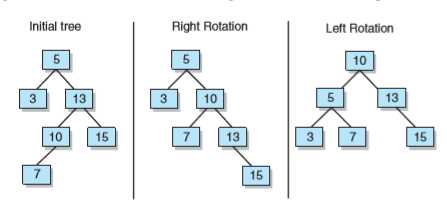
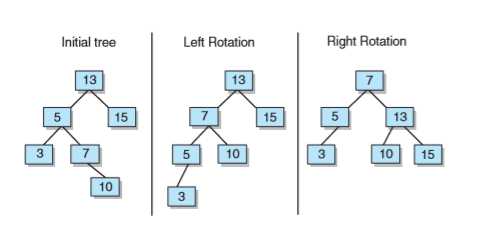
树(或树的任何子树)只有两种途径变得不平衡:插入结点或删除结点。因此在每次进行这两种操作时,都必须更新平衡因子,然后从插入或删除结点的那个地方开始检查树的平衡性。上溯到根结点,所以AVL树通常最好实现为每个结点都包含一个指向父结点的引用。
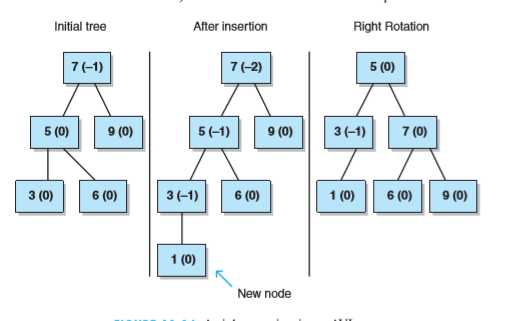
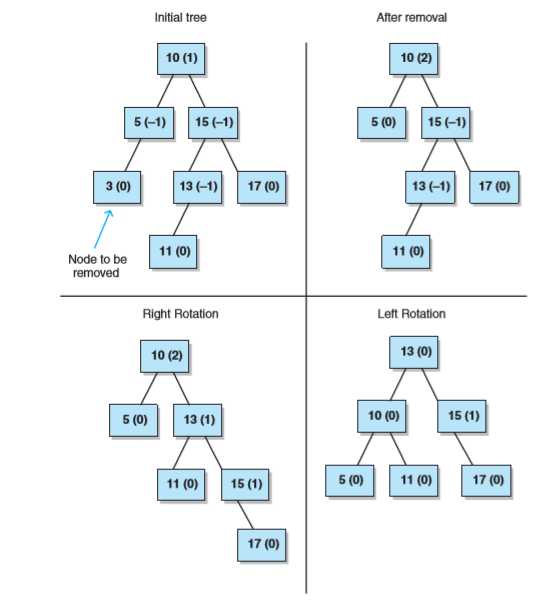
红黑树示意:
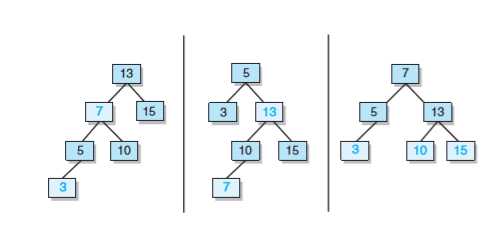
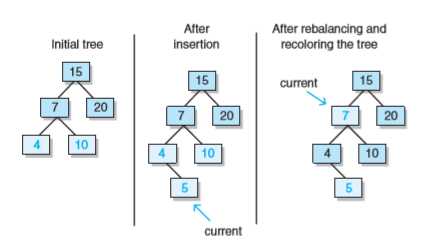
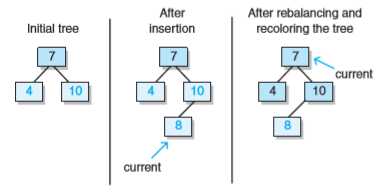
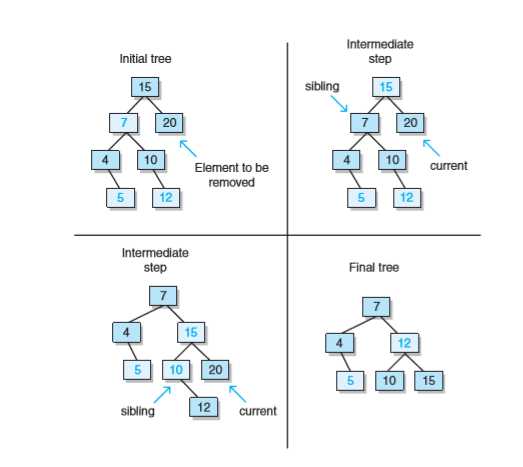
问题二解决:
public T removeElement(T targetElement) {
T result = null;
if (isEmpty()) {//树为空时抛出异常
throw new ElementNotFoundException("LinkedbinarySearchTree");
} else {//树不为空
BinaryTreeNode<T> parent = null;
if (((Comparable<T>) targetElement).equals(root.getElement())) {//要删除的元素是根结点
result = root.element;
BinaryTreeNode<T> temp = replacement(root);
if (temp == null) {//找不到结点替换
root = null;
} else {
//用找到的结点替换根结点
root.element = temp.element;
root.setLeft(temp.getLeft());
root.setRight(temp.getRight());
}
modCount--;
} else {//要删除根节点的孩子
parent = root;
if (((Comparable<T>) targetElement)
.compareTo(root.getElement()) < 0) {//目标在根的左边
result = removeElement(targetElement, root.getLeft(),
parent);
} else {//目标在根的右边
result = removeElement(targetElement, root.getRight(),
parent);
}
}
}
return result;
}
private T removeElement(T targetElement, BinaryTreeNode<T> node,
BinaryTreeNode<T> parent) {//用来删除除根以外的目标元素
T result = null;
if (node == null) {
throw new ElementNotFoundException("LinkedbinarySearchTree");
} else {
if (((Comparable<T>) targetElement).equals(node.getElement())) {//找到目标元素
result = node.element;
BinaryTreeNode<T> temp = replacement(node);//将node元素删除
//往下继续查找目标元素,看看左右孩子是否是
if (parent.right == node) {
parent.right = temp;
} else {
parent.left = temp;
}
modCount--;
} else {//如果目标元素比根结点小,则在根结点左侧,再次使用该方法从左子树中查找目标元素
parent = node;
if (((Comparable<T>) targetElement)
.compareTo(root.getElement()) < 0) {
result = removeElement(targetElement, root.getLeft(),
parent);
} else {//目标元素比根结点大,再次使用该方法从右子树中查找目标元素
result = removeElement(targetElement, root.getRight(),
parent);
}
}
}
return result;
}
// 删除元素
private BinaryTreeNode<T> replacement(BinaryTreeNode<T> node) {
BinaryTreeNode<T> result = null;
if ((node.left == null) && (node.right == null)) {//如果左右子树都为空,该元素没有孩子,直接返回空删掉它即可
result = null;
} else if ((node.left != null) && (node.right == null)) {只有左孩子时,将父结点指向左孩子
result = node.left;
} else if ((node.left == null) && (node.right != null)) {//只有右孩子时,将父结点指向右孩子
result = node.right;
} else {/* 先找到其右子树的最左孩子(或者左子树的最右孩子),即左(右)子树中序遍历时的第一个节点,然后将其与待删除的节点互换,最后再删除该节点(如果有右子树,则右子树上位)。总之就是先找到它的替代者,找到之后替换这个要删除的节点,然后再把这个节点真正删除掉。*/
BinaryTreeNode<T> current = node.right;//初始化右侧第一个结点
BinaryTreeNode<T> parent = node;
//获取右边子树的最左边的结点
while (current.left != null) {
parent = current;
current = current.left;
}
current.left = node.left;
// 如果当前待查询的结点
if (node.right != current) {
parent.left = current.right;// 整体的树结构移动就可以了
current.right = node.right;
}
result = current;
}
return result;
}问题三解决:在课堂上,老师提到了前驱结点,就是对一棵树进行中序排序,形成一个序列,书上所提到的返回中序后继者的意思就是排序后的序列的被删除结点的前驱结点或后驱结点都可以,由自己来定义。例如

对这棵树进行中序排序为:2 3 4 5 6。删除结点3后,可以返回前驱结点2,也可以返回后驱结点4。
20172314 2018-2019-1《程序设计与数据结构》第七周学习总结
标签:老师 -- 对象 最好 两种 因此 过程 private 迭代
原文地址:https://www.cnblogs.com/YiYiYi/p/9896248.html