标签:素数 alt fir 怎么 引用 current 意图 创建 需要
二叉查找树(binay scarch tree)是种带有附加属性的二叉树,即对树中的每个结点,其左孩子都要小于其父结点,而父结点又小于或等于其右孩子。
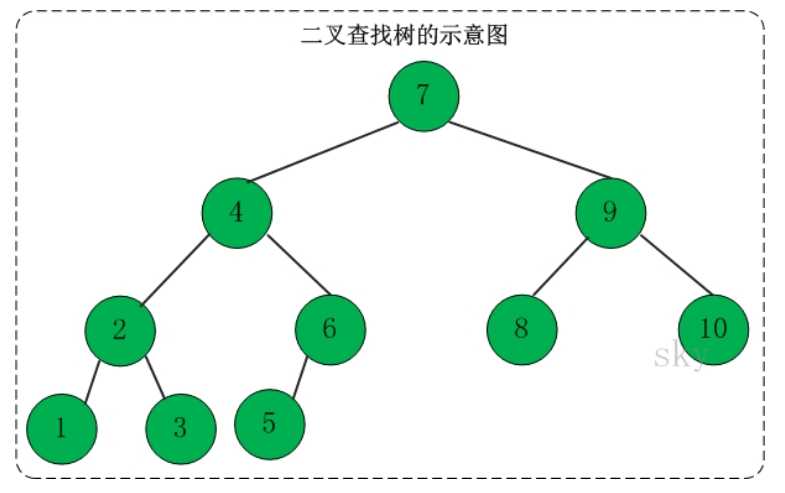
二叉查找树的定义是上章中讨论的二叉树定义的扩展。因此,下面的操作是二叉树中已定义的那些操作的补充。二叉查找树和平衡二叉查找树的接口是一样的程序列表。
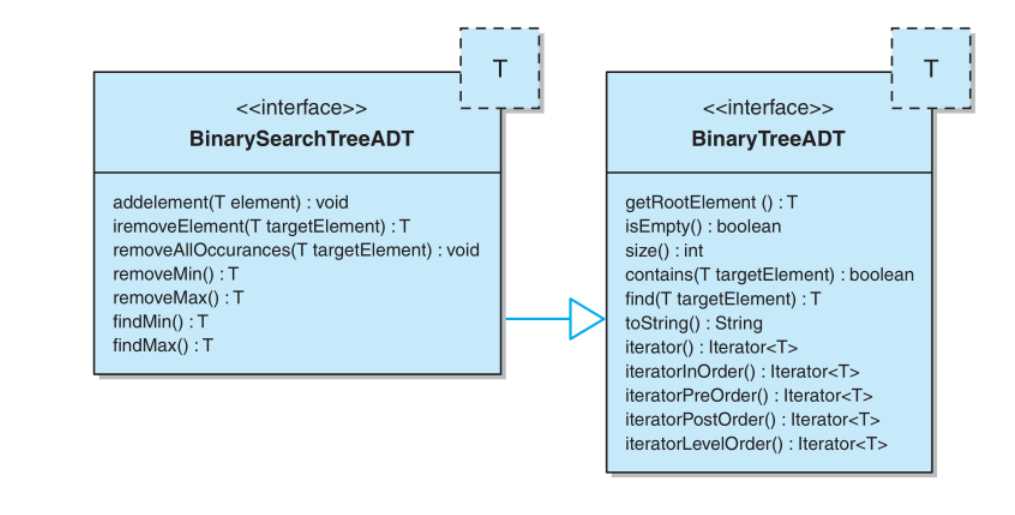
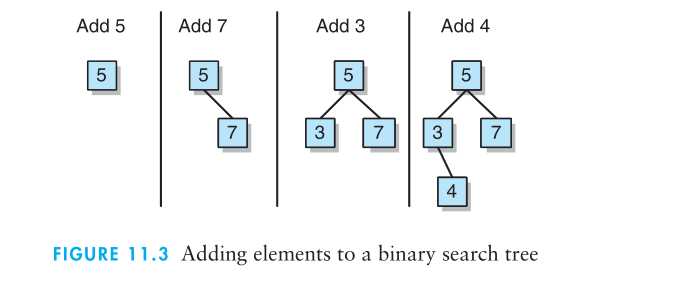
二叉查找树的最右侧结点会存放最大元素,而其最左侧结点会存放最小元素.
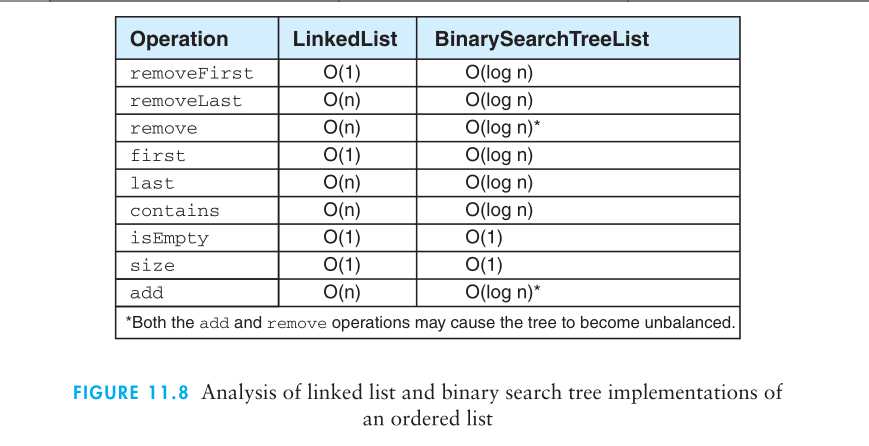
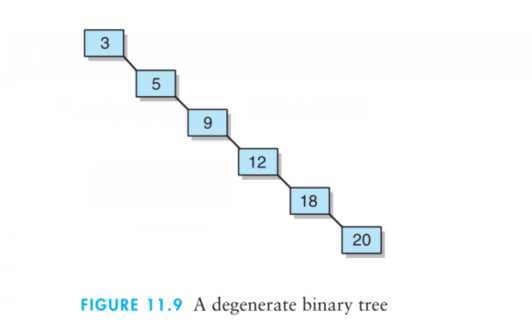
如果二叉查找树不平衡,其效率可能比线性结构的还要低。
平衡二叉树:任何一个节点的左右子树深度差不超过1.通过这个限定,阻止了二叉树的左右子树深度差较大的情况,维持了二叉树的稳定。
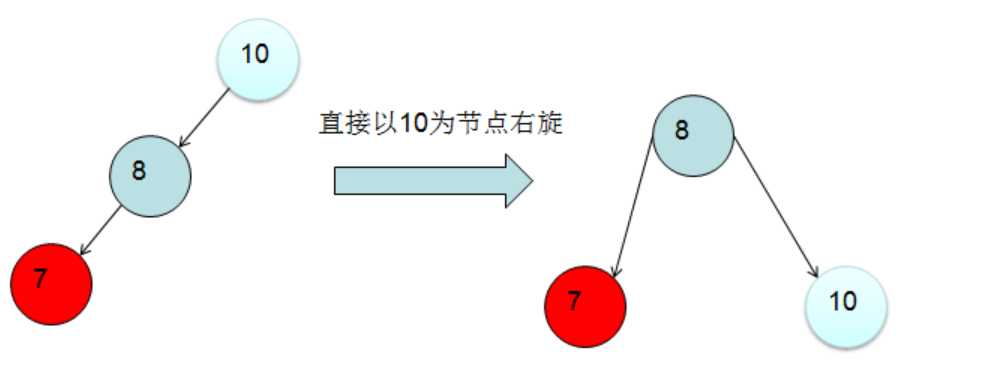
右旋:节点插入在最小不平衡树的右子树的右子树上面。
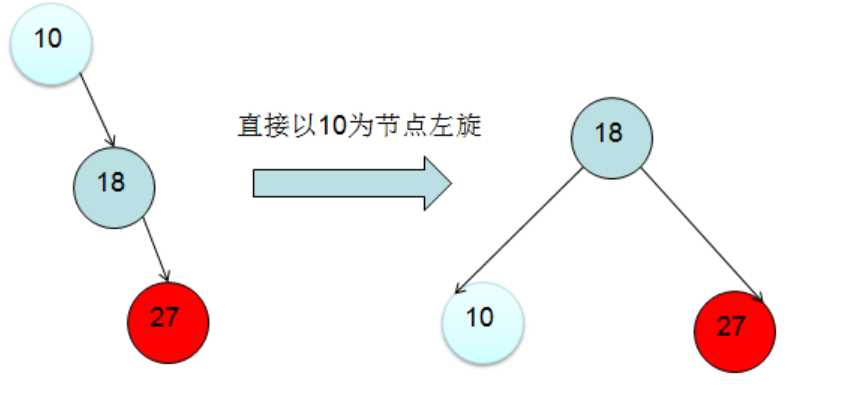
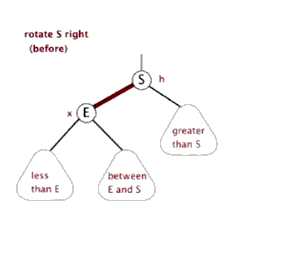
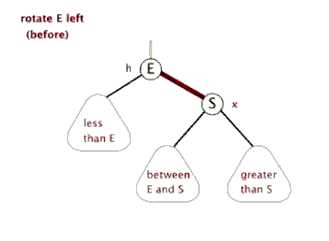
左旋:节点插入在最小不平衡节点的左子树的左子树上。
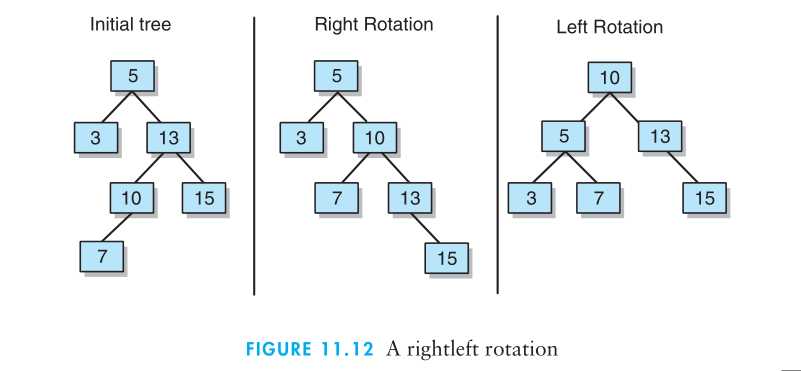
右左旋:节点插入在最小不平衡树的右子树的左子树上面。
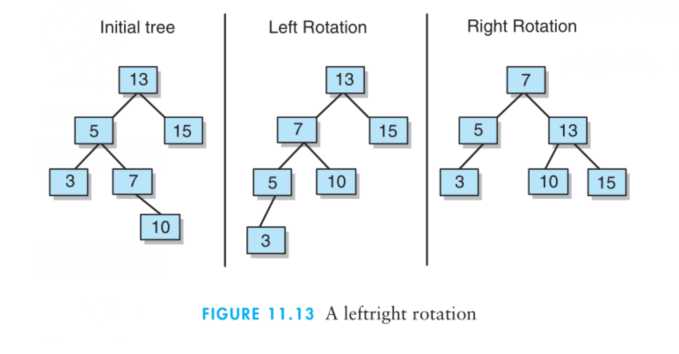
左右旋:节点插入在最小不平衡节点的左子树的右子树上面
用法总结:从发生不平衡的结点起,沿刚才回溯的路径取直接下两层的结点,如果这三个结点在一条直线上,则采用单旋转进行平衡化,如果这三个结点位于一条折线上,则采用双旋转进行平衡化。如图:
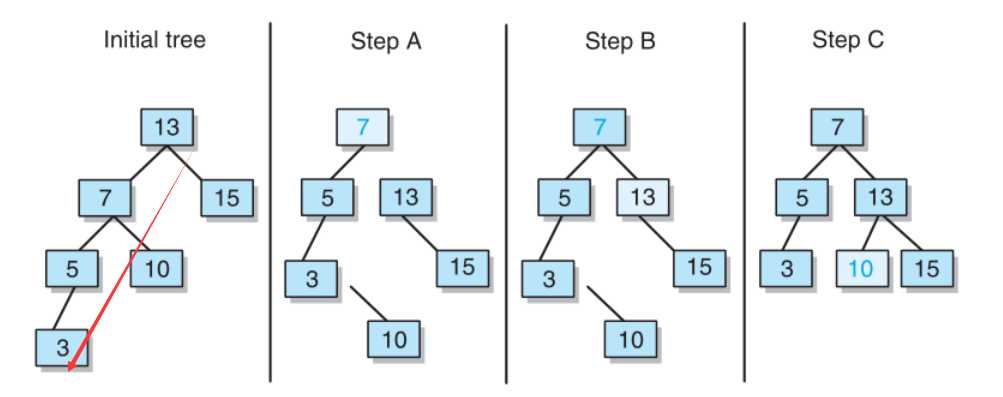
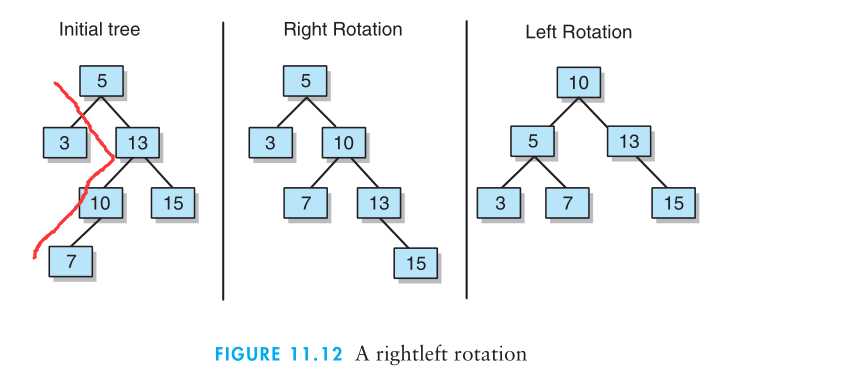
这是一篇很好的参考资料:数据结构——平衡二叉树
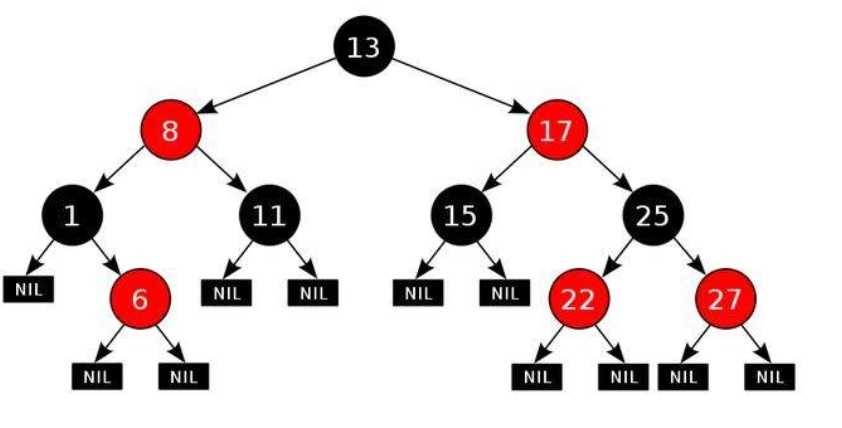
问题1:对课本removeElement方法的代码理解有困难,主要是后面的删除元素的图给错了,于是理解了半天。
问题1解决方案:其实最重要的是replacement代码段的理解,课本给出了三种情况的分类,“如果被删除结点有两个孩子,则replacement 会返回中序后继者”这种类型的时候中序后继者是什么意思呢?我结合着课本给出的删除结点的示意图来理解。
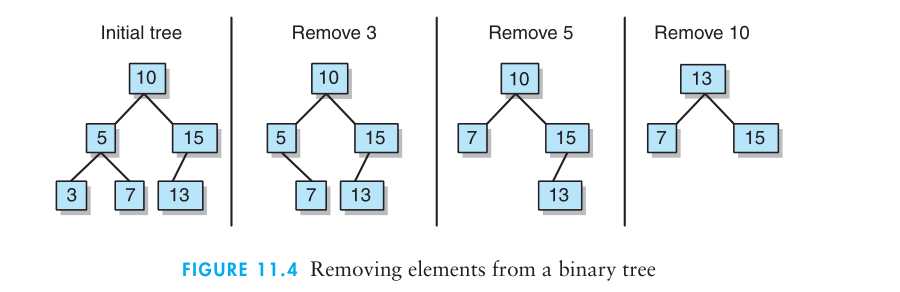
如果删除的节点是10,它有左右孩子,中序遍历是先查左孩子,再是该节点,然后是右孩子,中序遍历查找的顺序是7,10,13,15 。现在10是当前所指向的结点,所以从这个步骤开始,继续接下去的遍历,也就是看下一个查找的元素,然后返回它,也就是返回13 。
private BinaryTreeNode<T> replacement(BinaryTreeNode<T> node)
{
BinaryTreeNode<T> result = null;
// 如果被删除结点没有孩子
if ((node.left == null) && (node.right == null))
result = null;
//被删除的结点只有一个孩子,则返回孩子
else if ((node.left != null) && (node.right == null))
result = node.left;
else if ((node.left == null) && (node.right != null))
result = node.right;
//被删除结点有两个孩子,就要找的比左边孩子小,但比该结点大的孩子。
else
{
BinaryTreeNode<T> current = node.right;//创建一个结点current,存放当前节点的右孩子
BinaryTreeNode<T> parent = node;
while (current.left != null)//中序遍历找到下一个结点
{
parent = current;
current = current.left;
}
current.left = node.left;//将被删除结点的左孩子链到找到的这个结点的左边
if (node.right != current)//如果这个找到的节点不是原要被删除的结点的右孩子
{
parent.left = current.right;//这时current.right为null,parent.left从被找到的结点变为null
current.right = node.right;
}
result = current;
}
return result;
}红黑树中元素的插入:
1.首先插入结点。插入的结点定为红色( 因为将插入的节点着色为红色,不会违背"从树根到树叶的所有路径上包含相同数目的黑色结点。",少违背一条特性,就意味着我们需要处理的情况越少)。
2.插入结点后的红黑树仍是一棵二叉查找树,但是插入后变得不再平衡了。之后重新平衡化或者说重新着色的过程则是一种迭代的过程,所以插入节点后,我们要做的就是将破坏红黑树规则的结点通过重新着色上移到别的结点。
3.接下来是分情况讨论如何变色和旋转,使其重新平衡。
(1)其父节点为black,这种情况下没有违背红黑树任何条件,直接插入即可(包含被插入的节点为根节点的情况);
(2)插入的结点的父节点是red的情况下,又可根据叔叔结点的case划分为三种情况来处理;
- case1:当叔叔结点也为红色时,第一,先将父节点和叔叔结点变为black;第二,将祖父结点变为red;最后运用递归继续改变更底层的结点。
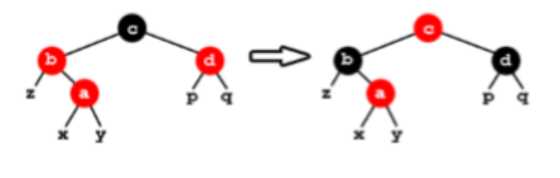
- case2:当叔叔结点是black时,如果当前结点是父节点的左孩子,则将父节点染为black,在把祖父结点染为red,最后以祖父节点为支点进行右旋。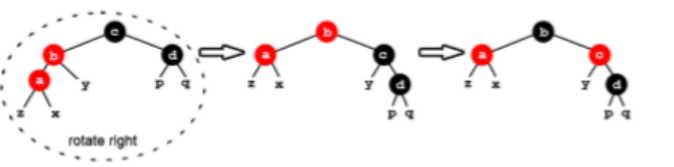
- case3:当叔叔结点是black时,而当前结点是父节点的右孩子,则以该插入的结点的父节点作为当前节点进行左旋,变为case2进行处理。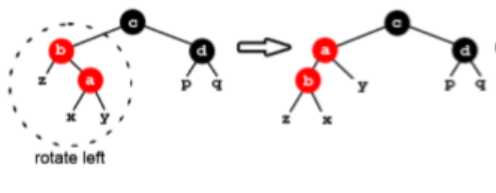
调整的方式:
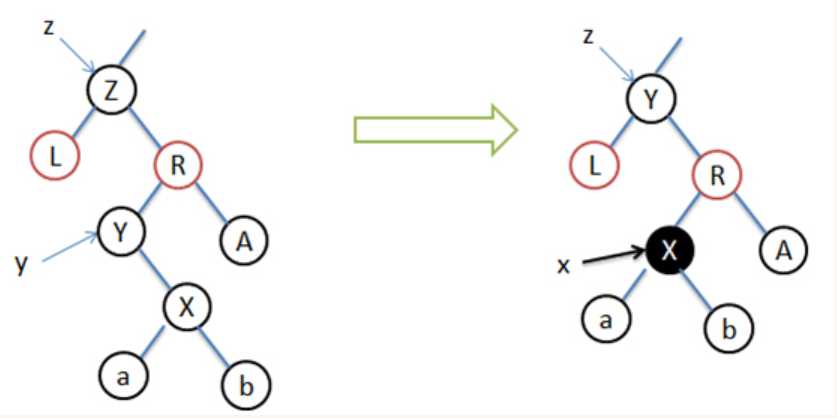
在第三种情况中,通过使用z的后继节点y替换z节点,然后使用y的右孩子x来填补y的位置。在此过程需要将节点y进行移动,由于移动之后的y节点保持原来z节点的颜色,而x节点在代替y节点之后可能会出现问题,当然只会在y节点是黑色的情况下才会出现问题,当y节点为红色时,移动时红黑树的性质不会被破坏,y节点为黑色时,一定会出现黑高的不相等,并且也可能会出现两个连续的红色节点。这时需要对其进行下一步调整。
红黑树的删除
这是关于删除的一份资料,跟着这里面看可以理解很多,但自己还是有些内容理解不了,主要是删除比插入的情况更多而且更复杂,理解起来还是很有难度的。
(statistics.sh脚本的运行结果截图)
这周的学习是建立在上周所学知识的基础上的,果然基础要打好,后面的学习才会更有效率。不得不批评一下淘宝买来的课本了,太坑爹了,图错了好几个,我一直研究,一直觉得不对,后来事实证明我是正确的,不过还是浪费了一些时间在这个上面。双周的课程比单周要少一些,所以这周自学Java的时间要多一些,果然知识都是靠时间换来的。
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | ||
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 10/10 | |
| 第二周 | 326/326 | 1/2 | 18/28 | |
| 第三周 | 784/1110 | 1/3 | 25/53 | |
| 第四周 | 2529/3638 | 2/5 | 37/90 | |
| 第五周 | 1254/4892 | 2/7 | 20/110 | |
| 第六周 | 1403/6295 | 2/9 | 32/142 | |
| 第七周 |
计划学习时间:30小时
实际学习时间:XX小时
改进情况:
20172310 2017-2018《程序设计与数据结构》(下)第七周学习总结
标签:素数 alt fir 怎么 引用 current 意图 创建 需要
原文地址:https://www.cnblogs.com/Qiuxia2017/p/9880422.html