标签:out ORC span while pre 相等 序列 typedef 情况
给出一个数字序列,找出一个区间,当删除这个区间中的两个相同的数字后,只保留这两个数字之间的序列,然后继续删除相同的数字,问最多可以实行多少次删除操作。
例如:
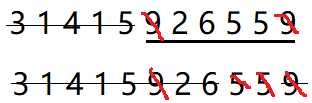
所以执行两次删除操作。
思路:
区间dp,关键在于确定大的区间是由哪些小的区间转化来的。
当a[l] == a[r]的时候,dp[l][r] = dp[l+1][r-1]+1(因为要得到最多的删除次数,大的区间的次数在相等的情况下肯定是由内部小的区间加一得来的);
当a[l] != a[r]的时候,dp[l][r] = max(dp[l+1][r],dp[l][r-1])(这个自己模拟的出的......)
代码:
内层循环枚举长度:

#include <bits/stdc++.h> #define inf 0x3f3f3f3f #define FRE() freopen("in.txt","r",stdin) using namespace std; typedef long long ll; const int maxn = 5000+10; int dp[maxn][maxn]; int a[maxn]; int main(){ //FRE(); int n; while(scanf("%d",&n)!=EOF){ for(int i=1; i<=n; i++){ scanf("%d",&a[i]); } for(int i = 1; i<=n; i++){ for(int j = 1; j<=n; j++){ dp[i][j] = 0; } } //memset(dp,0,sizeof(dp)); for(int k=1; k<n; k++){//枚举区间长度 for(int l=1; l+k<=n; l++){//枚举区间的起点 if(a[l] == a[l+k]){ dp[l][l+k] =dp[l+1][l+k-1]+1; } else{ dp[l][l+k] = max(dp[l+1][l+k],dp[l][l+k-1]); } } } printf("%d\n",dp[1][n]); } return 0; } /* PutIn: 3 6 6 6 12 3 14 15 92 65 35 89 79 32 38 46 26 12 3 1 4 1 5 9 2 6 5 3 5 9 7 2 7 1 8 2 8 1 4 1 6 1 8 11 1 2 4 8 16 32 16 8 4 2 1 6 1 2 3 1 2 3 PutOut: 1 0 2 2 1 5 1 */
内层循环枚举区间右端点

#include <bits/stdc++.h> #define inf 0x3f3f3f3f #define FRE() freopen("in.txt","r",stdin) using namespace std; typedef long long ll; const int maxn = 5e3+10; int dp[maxn][maxn]; int a[maxn]; int main(){ //FRE(); int n; while(scanf("%d",&n)!=EOF){ for(int i=1; i<=n; i++){ scanf("%d",&a[i]); } for(int i = 1; i<=n; i++){ for(int j =1; j<=n; j++){ dp[i][j] = 0; } } for(int l=n; l>=0; l--){//只能逆序来枚举起点,正序大区间的值无法更新 for(int r=l+1; r<=n; r++){ if(a[l] == a[r]){ dp[l][r] = dp[l+1][r-1]+1; }else { dp[l][r] = max(dp[l+1][r],dp[l][r-1]); //dp[l][r] = max(dp[l][r-1],dp[l][r]); } } } printf("%d\n",dp[1][n]); } return 0; }
区间dp过程大致相同:
第一层循环枚举区间的长度,第二层循环枚举区间的起点。
第二层又有两种情况:
第一种:需要在[st,en]中找一个分割点k使得将[st,en]分成[st,k]和[k+1,en]这样两个区间能够得到最优解。
第二种:[i,j]可以由[i,j-1]或者[i,j+1]转移过来。这种转移关系肯定是有具体的情况推出的,不是一成不变的。
Gym - 101670F Shooting Gallery(CTU Open Contest 2017 区间dp)
标签:out ORC span while pre 相等 序列 typedef 情况
原文地址:https://www.cnblogs.com/sykline/p/9898398.html