标签：分析   string   实现   不可   class   tab   java数据结构   text   .net   

学号 20172326 《程序设计与数据结构》第七周学习总结

教材学习内容总结

AVL树

• AVL树是实现平衡二叉树的一种算法实现，别的方法也可实现例如红黑树。
• 平衡因子：右子树高度-左子树高度的差值（高度是指当前结点到叶子结点的最长路径，如所有叶子结点的高度都为0，而深度则是指从根结点到当前结点的最大路径，如根结点的深度为0。），规定AVL树的平衡因子不大于1。所以在一个已经实现的AVL树中，任意一个节点的平衡因子的取值为（1，-1,0）。
• 左旋，右旋，左右旋，右左旋。当进行插入抑或是删除操作时，可能导致一个平衡二叉树失衡，因此就要对其进行调整，使其恢复平衡。可以简单的用列表遍历这个数，重新构造一个新的树，但这种方法太过简单，粗暴。所以我们可以使用旋转树，来使其恢复平衡。
• 右旋（或称为左左旋），经过计算，发现某一失衡点的左子树的深度大于右子树，这时就需要将左子树向“右”旋转，使其恢复平衡。方法：将失衡点的左结点设为当前树的新根，使原根变为新根的右结点，将新根的右结点变为原根的左结点。
• 左旋，失衡点处右子树的深度大于左子树，将右子树向左旋转。原理与右旋对称。
• 当某一子树太深时，仅通过一次右旋或左旋将无法完成，因此，我们需要使用两次旋转来实现它。因为旋转方法总是对称的，所以，只拿左右旋转为例。
• 左右旋，当左孩子的右子树太深时，进行旋转。先将其父节点变为其左孩子，同时将其左左孩子进行分配。

• 在执行结束操作后，通过比较每个结点的平衡因子来维持AVL树的平衡

  红黑树

• 根结点为黑色；每个结点只有红色或黑色；所有的叶结点为黑色；红结点的孩子均为黑色；对于每个结点，从该结点到其叶子结点构成的所有路径上的黑结点个数相同；
• 插入结点。1.插入结点为对应的根结点，直接将其涂黑即可。2.插入结点的父节点为黑结点，那么，直接插入即可。3.插入的父节点为红色。此时将破坏红黑树的结构，因此需要将其进行旋转。 分为以下三种情况，满足之一的条件时，进行递归。
• • 当插入结点的父结点为红，且叔结点也为红时，将其父结点与叔结点改为红色，祖父结点变为黑色。并将带操作结点改为祖父结点
• • 当待操作结点的父节点是红色的，叔叔节点是黑色的，且插入节点是其父节点的右子节点。这时，将待操作结点改为其父结点，再将带操作结点左旋。
• • 待操作结点的父结点是红色，叔叔结点是黑色，且插入结点是其父结点的左子结点。我们要做的操作有：将当前结点的父结点涂黑，将祖父结点涂红，在祖父结点为支点做右旋操作。最后把根结点涂黑，整个红-黑树重新恢复了平衡。
• 

• 

• 删除操作：
• • 第一步：将红黑树当作一颗二叉查找树，将节点删除。
    这和"删除常规二叉查找树中删除节点的方法是一样的"。分3种情况：
    ① 被删除节点没有儿子，即为叶节点。那么，直接将该节点删除就OK了。
    ② 被删除节点只有一个儿子。那么，直接删除该节点，并用该节点的唯一子节点顶替它的位置。
    ③ 被删除节点有两个儿子。那么，先找出它的后继节点；然后把“它的后继节点的内容”复制给“该节点的内容”；之后，删除“它的后继节点”。在这里，后继节点相当于替身，在将后继节点的内容复制给"被删除节点"之后，再将后继节点删除。这样就巧妙的将问题转换为"删除后继节点"的情况了，下面就考虑后继节点。 在"被删除节点"有两个非空子节点的情况下，它的后继节点不可能是双子非空。既然"的后继节点"不可能双子都非空，就意味着"该节点的后继节点"要么没有儿子，要么只有一个儿子。若没有儿子，则按"情况① "进行处理；若只有一个儿子，则按"情况② "进行处理。
• • 第二步：通过"旋转和重新着色"等一系列来修正该树，使之重新成为一棵红黑树。
    因为"第一步"中删除节点之后，可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树，使之重新成为一棵红黑树。

• 

教材学习中的问题和解决过程

• 问题1：

Comparable<T> comparableElement = (Comparable<T>)element  

为什么要使用comparable来将element转为相关格式呢？

• 问题1理解：这是添加元素方法（addElement）的一部分代码，将传入的参数转化为comparable型。为什么不在传入的时候直接将其变为comparable类型呢?况且直接变为comparable型数据，在之后的维护平衡树时有助于进行插入元素之间的比较。我们知道，在方法中传入一个comparable参数看似简单，但在真正通过输入数据的时候，可能是一个string值，也可能是一个int值，但是，想传入一个comparable类型数据，基本不可能，所以，选择了在方法中进行类型转化。
• 问题2:红黑树的平衡问题
• 问题2理解：首先，我们知道，红黑树通过颜色来控制平衡。尤其是黑色结点，通过每条路径有相同数目的黑色结点。同时，每个红色结点的孩子结点为黑色。可以想象，想沿着一边子树的一个方向插入众多的结点将不可实现，从而实现了平衡。同时，根据二叉查找树的性质可知，若删除一个结点，除非该结点为根结点且为红色，否则必需经过一些操作以维持平衡。
• 在课堂上，大家发现了一个问题。这种时候，应该怎样操作，对于结点（7）结点（8），无论将其变为黑色还是红色，都符合要求。那么，为什么还要将其涂为红色呢?

• 

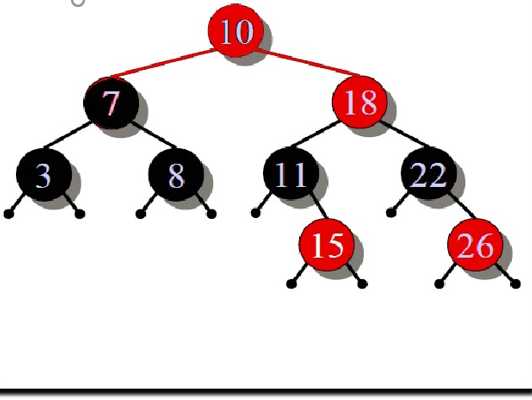
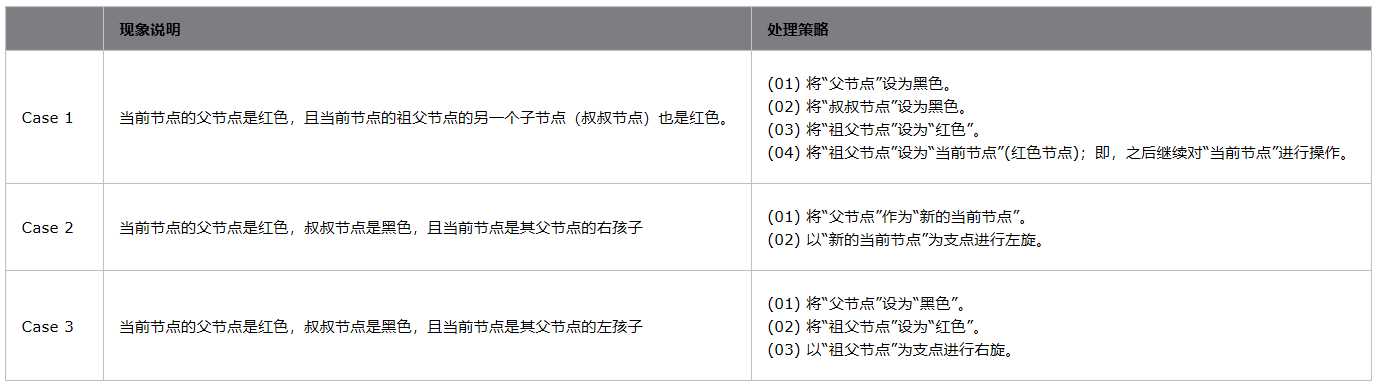
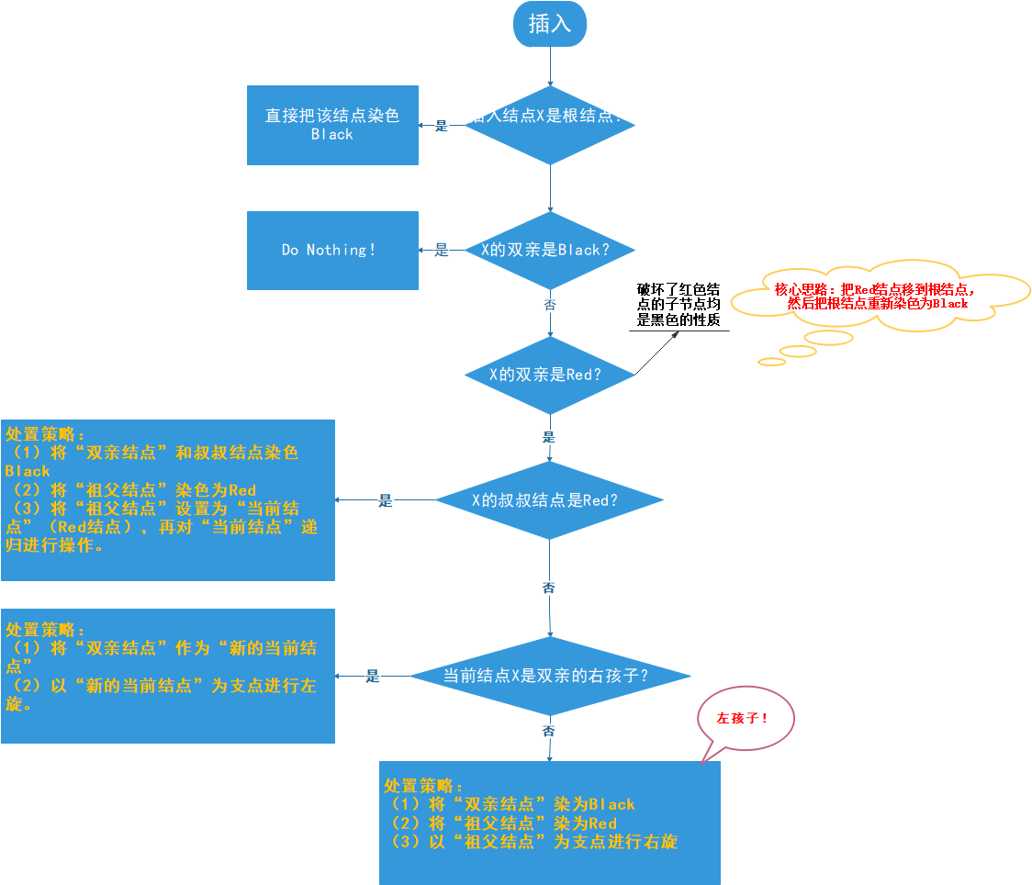
• 涂为红色，有什么变化呢？相较于涂为黑色，黑色结点减少，且其孩子结点为黑色。如果是黑色呢？该树整体黑色结点增多。但问题恰恰就在这里，如果这是一颗单独的树还好说，但如果是某一棵树的子树呢？只有这一部分的黑色结点增加，别的均不变，这直接导致违反了规定。所以，从中也可以看出，对于红黑树，黑色结点的变化是相当慎重的。从规定插入的结点默认为红色也可以看出这点。

代码托管

其他（感悟、思考等，可选）

• 本章的知识不好理解，尤其是红黑树，涉及了大量的不同情况，令人头秃，而且网上的知识有漏洞的也很多，继续自己体会。

  学习进度条

参考资料

• 红黑树详细分析，看了都说好
• java数据结构与算法之平衡二叉树(AVL树)的设计与实现

《程序设计与数据结构》第七周学习总结

标签：分析   string   实现   不可   class   tab   java数据结构   text   .net   

原文地址：https://www.cnblogs.com/326477465-a/p/9899047.html