标签：rate   问题   两种   目标   二叉查找树   节点   ima   基本原理   9.png   

20172322 《程序设计与数据结构》第七周学习总结

教材学习内容总结

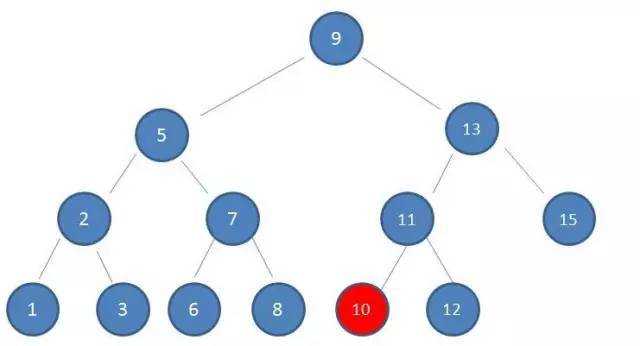
本章的内容主要讲二叉查找树，二叉查找树是对于二叉树的一种拓展，这意味着上一章中对于二叉树的操作对于二叉查找树同样适用，同时它也是一种带有附加属性的二叉树。这种附加属性即：对树中的每个结点，它的左孩子都要小于其父结点，而父结点又小于或等于它的右孩子。这意味着在所有比根结点大的元素都存在于根结点的左边，而比根结点小的元素都在根结点的右边。如图所示：

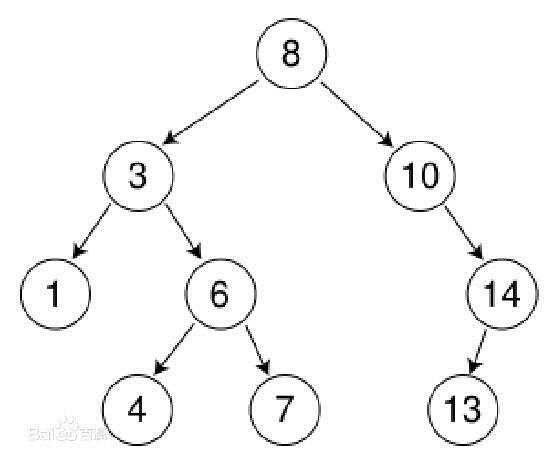
值得一提的是，对二叉查找树进行中序遍历，正好可以得到一队递增排序的元素。

例如，对于之前所示二叉查找树进行中序遍历可以等到：1，3，4，6，7，8，10，13，14。

• 二叉查找树的查找算法：因为二叉查找树的每个结点都具有特殊性质，所以说所有的元素都是以一定的顺序存在于二叉查找树中，所以对于比根结点大的元素就去根结点的左子树查找，对于比根结点小的元素就去根结点的右子树查找，这个算法如果使用递归实现会非常方便。

例如，查找10

1.查看根节点9：

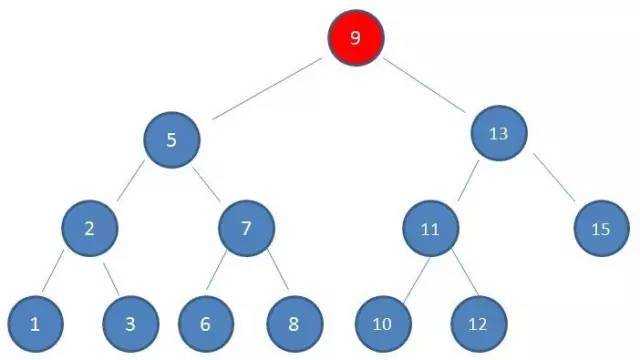
2.由于10 > 9，因此查看右孩子13：

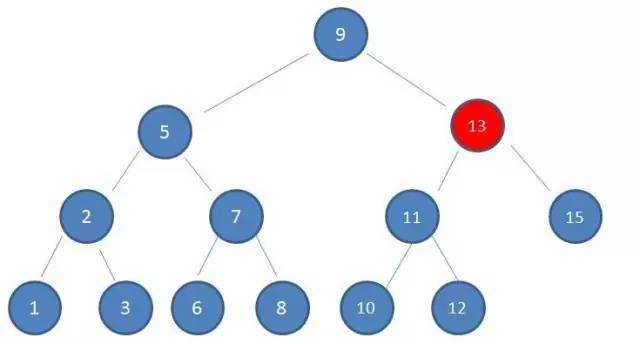
3.由于10 < 13，因此查看左孩子11：

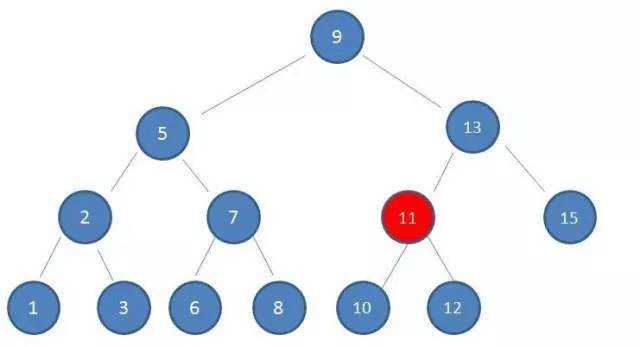
4.由于10 < 11，因此查看左孩子10，发现10正是要查找的节点：

• 二叉查找树的插入算法：因为二叉查找树是一个其结点具有特定属性的二叉树所以它的插入算法就只需要一个方法，我觉得二叉查找树与有序列表类似，仅需一个addElement方法就可以把一个元素插入正确的位置。具体的解决方案是：
  • 首先执行查找算法，找出被插结点的父亲结点。
  • 判断被插结点是其父亲结点的左、右儿子。将被插结点作为叶子结点插入。
  • 若二叉树为空。则首先单独生成根结点。
• 二叉查找树的删除算法：删除结点有三种情况分别是需要删除的结点是叶结点，是仅有左子树/右子树的结点，是既有左子树又有右子树的结点。
  • 删除的结点是叶结点，直接让树结点的父结点的下一个指向null即可。
  • 删除的结点是仅有左子树/右子树的结点，将该节点删除后，将该结点的左结点/右结点提到被删除结点的位置即可。
  • 删除的结点是既有左子树又有右子树的结点，这个时候需要用到中序遍历后的前驱结点，将前驱结点提到被删除结点的位置。

• 平衡二叉查找树，它存在的意义在于提升效率，例如，一棵蜕化树看起来更像一个链表但是它的效率比链表还差。

  • 如图所示，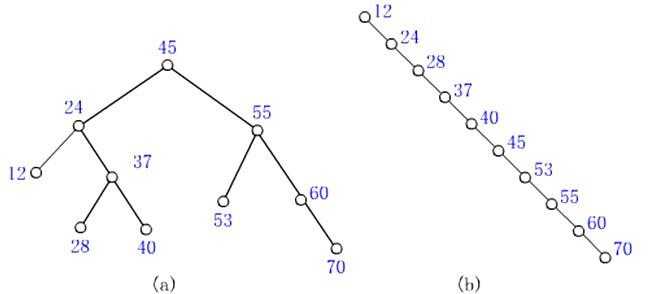

  • 对于一个平衡二叉查找树来说，它的查找效率会比第二种蜕化树高很多，因为在蜕化树中的每个结点附带有额外的开销，所以说我们就要想着将一些树尽可能的改变为平衡二叉查找树。将一个费平衡二叉查找树改变成为二叉查找树主要有四种方法：右旋，左旋，左右旋，右左旋。

    • 在提到四种方法之前，有一个概念需要理解，一个平衡二叉查找树的最大路径长度应该为log₂n（n为元素个数），并且最长路径必须不小于log₂n-1（n为元素个数），如果一个树的最长查找路径大于log₂n则表明它不平衡，这时候就需要一定的操作使其平衡。

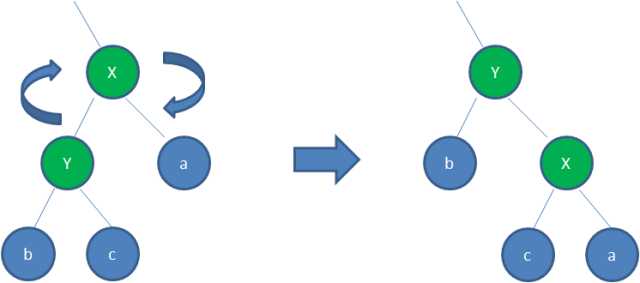
    • 右旋，通常是指左孩子绕着其父结点向右旋转，一般适用于左子树长于右子树的情况
      

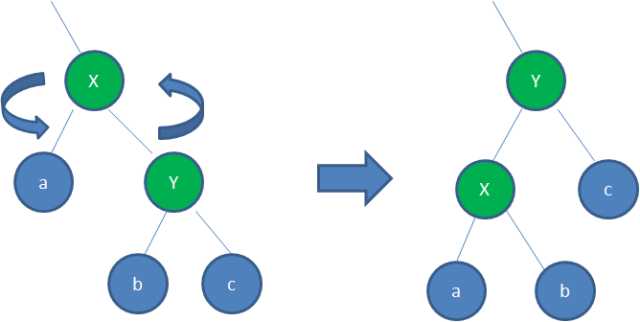
    • 左旋，通常是指右孩子绕着其父结点向左旋转，一般适用于右子树长于左子树的情况
      

• AVL树，在之前的基础上添加了平衡因子的说法，即左右子树的高度差，如果高度差大于1或者小于-1，则以该结点为树根的子树需要重新平衡。

• 红黑树，顾名思义，即给每个结点赋以红和黑两种颜色，对于红黑树的三点规定如下，
  • 根结点为黑色。
  • 红色节点的孩子为黑色。
  • 从树根到树叶的每条路径都包含同样树木的黑色结点。
• 红黑树的插入，总是把插入的新元素的颜色设为红色，在插入过后极大可能会导致一系列操作以再次平衡红黑树。

• 红黑树的删除，与插入类似，删除一个元素后有极大可能需要一系列操作以再次平衡红黑树。

教材学习中的问题和解决过程

• 问题一：对于红黑树存在的意义问题，为什么要单独设置一个红黑树呢？红黑树可以解决的问题AVL树也同样可以解决。
• 问题一解决方案：这个问题我在网上查找了部分答案，发现为什么需要发明红黑树。
  • 最主要就是效率问题，红黑树并不追求“完全平衡”——它只要求部分地达到平衡要求，降低了对旋转的要求，从而提高了性能。
  • 当然这也不是没有代价的，红黑树是牺牲了严格的高度平衡的优越条件为代价让红黑树能够以O(log2 n)的时间复杂度进行搜索、插入、删除操作。

代码调试中的问题和解决过程

• 问题一：对于AVL树的实现存在一些问题，原本以为书上所给的代码已经实现了AVL树，就好像那个addElement(T element)一样。
• 问题一解决：询问了结对伙伴，发现好像不是这样的，addElement(T element)这个方法只能一直添加元素，但不能使得元素成为平衡树，就好像如果一直利用这个方法添加递减的元素会导致蜕化树的出现。
• 问题二：对于AVL树的实现有一些疑惑，它的左旋、右旋、左右旋、右左旋怎么实现？
• 问题二解决：班主任在蓝墨云上的资源《红黑树(五)之 Java的实现》的博主对于树的实现有一系列的东西，不只是红黑树，我在其博客中找到了《AVL树(三)之 Java的实现》，借鉴了博主的部分代码，并且看懂了他们，感谢博主

代码托管“点这里跳转到码云”

上周考试错题总结

• 错题1：A find operation on a balanced binary search tree is O(logn) where as a find operation for binary search tree without the balance assumption is O(n).
• A.True
• B.False

• 错题1解析：平衡树查找的时间复杂度就是O(logn)。

• 错题2是那一道没有图的题。

结对及互评（待修改）

• 博客中值得学习的或问题：
  • 范雯琪同学的博客课本上的学习内容总结部分写得十分详细，值得学习。
  • 每次看到范雯琪同学的博客自己都比较惭愧，实在是非常优秀，可想而知她在博客这一方面所做出的努力，我也非常想想她学习。
• 代码中值得学习的或问题：
  • commit提交的解释清晰明了，我觉得我应该学习。
  • 有许多代码的问题都是我向她询问，我很感谢她

点评过的同学博客和代码

• 本周结对学习情况

  • 20172303

  • 结对学习内容
    • 我们一起实现了本周需要实现的一些PP项目并且给互相讲述了其中的基本原理。

其他

• 感悟：感觉自己在代码上的问题越来越少了...快要找不出问题了，怎么办...一定是我学得还不够认真

课本单词

(本部分用于收集本章节后的生词)

• binary search tree：二叉查找树
• degenerate tree：蜕化树
• right rotation：右旋
• left rotation：左旋
• rightleft rotation：右左旋
• leftright rotation：左右旋
• AVL tree：AVL树
• balance factor：平衡因子
• red/black tree：红黑树

学习进度条

• 计划学习时间:25小时

• 实际学习时间:33小时

• 改进情况：规范commit行为，改进博客园模版。

参考资料

• 《Java软件结构与数据结构》
• 《红黑树(五)之 Java的实现》
• 《AVL树(三)之 Java的实现》

20172322 《程序设计与数据结构》第七周学习总结

标签：rate   问题   两种   目标   二叉查找树   节点   ima   基本原理   9.png   

原文地址：https://www.cnblogs.com/zhangyeye233/p/9898940.html