标签：center   mes   display   种类型   end   图片   play   数学基础   方向   

目录

• 线性代数
  • 一、基本知识
  • 二、向量操作
  • 三、矩阵运算

线性代数

一、基本知识

1. 本书中所有的向量都是列向量的形式：
   \[\mathbf{\vec x}=(x_1,x_2,\cdots,x_n)^T=\begin{bmatrix}x_1\\x_2\\ \vdots \\x_n\end{bmatrix}\] 本书中所有的矩 \(\mathbf X\in \mathbb R^{m\times n}\) 都表示为：
   \[\mathbf X = \begin{bmatrix} x_{1,1}&x_{1,2}&\cdots&x_{1,n}\x_{2,1}&x_{2,2}&\cdots&x_{2,n}\\vdots&\vdots&\ddots&\vdots\x_{m,1}&x_{m,2}&\cdots&x_{m,n}\\end{bmatrix}\] 简写为 \((x_{i,j})_{m\times n}\) 或 \([x_{i,j}]_{m\times n}\) 。
2. 矩阵的F范数：设矩 \(\mathbf A=(a_{i,j})_{m\times n}\) ，则其F范数为 \(||\mathbf A||_F=\sqrt{\sum_{i,j}a_{i,j}^{2}}\) 。
   它是向量 \(L_2\) 范数的推广。
3. 矩阵的迹：设矩 \(\mathbf A=(a_{i,j})_{m\times n}\) ， $ \mathbf A$ 的迹为 \(tr(\mathbf A)=\sum_{i}a_{i,i}\) 。
   迹的性质有：
   • \(\mathbf A\) 的F 范数等 \(\mathbf A\mathbf A^T\) 的迹的平方根 \(||\mathbf A||_F=\sqrt{tr(\mathbf A \mathbf A^{T})}\) 。
   • \(\mathbf A\) 的迹等 \(\mathbf A^T\) 的迹 \(tr(\mathbf A)=tr(\mathbf A^{T})\) 。
   • 交换律：假设 \(\mathbf A\in \mathbb R^{m\times n},\mathbf B\in \mathbb R^{n\times m}\) ，则有 \(tr(\mathbf A\mathbf B)=tr(\mathbf B\mathbf A)\) 。
   • 结合律 \(tr(\mathbf A\mathbf B\mathbf C)=tr(\mathbf C\mathbf A\mathbf B)=tr(\mathbf B\mathbf C\mathbf A)\) 。

二、向量操作

1. 一组向 \(\mathbf{\vec v}_1,\mathbf{\vec v}_2,\cdots,\mathbf{\vec v}_n\) 是线性相关的：指存在一组不全为零的实 \(a_1,a_2,\cdots,a_n\) ，使得 \(\sum_{i=1}^{n}a_i\mathbf{\vec v}_i=\mathbf{\vec 0}\) 。
   一组向 \(\mathbf{\vec v}_1,\mathbf{\vec v}_2,\cdots,\mathbf{\vec v}_n\) 是线性无关的，当且仅 \(a_i=0,i=1,2,\cdots,n\) 时，才有 \(\sum_{i=1}^{n}a_i\mathbf{\vec v}_i=\mathbf{\vec 0}\) 。
2. 一个向量空间所包含的最大线性无关向量的数目，称作该向量空间的维数。

3. 三维向量的点积 \(\mathbf{\vec u}\cdot\mathbf{\vec v} =u _xv_x+u_yv_y+u_zv_z = |\mathbf{\vec u}| | \mathbf{\vec v}| \cos(\mathbf{\vec u},\mathbf{\vec v})\) 。
   

   

4. 三维向量的叉积：
   \[\mathbf{\vec w}=\mathbf{\vec u}\times \mathbf{\vec v}=\begin{bmatrix}\mathbf{\vec i}& \mathbf{\vec j}&\mathbf{\vec k}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{bmatrix}\] 其 \(\mathbf{\vec i}, \mathbf{\vec j},\mathbf{\vec k}\) 分别 \(x,y,z\) 轴的单位向量。
   \[\mathbf{\vec u}=u_x\mathbf{\vec i}+u_y\mathbf{\vec j}+u_z\mathbf{\vec k},\quad \mathbf{\vec v}=v_x\mathbf{\vec i}+v_y\mathbf{\vec j}+v_z\mathbf{\vec k}\] ?
   • $\mathbf{\vec u} $ 和 \(\mathbf{\vec v}\) 的叉积垂直于 \(\mathbf{\vec u},\mathbf{\vec v}\) 构成的平面，其方向符合右手规则。
   • 叉积的模等于 \(\mathbf{\vec u},\mathbf{\vec v}\) 构成的平行四边形的面积
   • \(\mathbf{\vec u}\times \mathbf{\vec v}=-\mathbf{\vec v}\times \mathbf{\vec u}\)
   • $\mathbf{\vec u}\times( \mathbf{\vec v} \times \mathbf{\vec w})=(\mathbf{\vec u}\cdot \mathbf{\vec w})\mathbf{\vec v}-(\mathbf{\vec u}\cdot \mathbf{\vec v})\mathbf{\vec w} $
     
5. 三维向量的混合积：
   \[[\mathbf{\vec u} \;\mathbf{\vec v} \;\mathbf{\vec w}]=(\mathbf{\vec u}\times \mathbf{\vec v})\cdot \mathbf{\vec w}= \mathbf{\vec u}\cdot (\mathbf{\vec v} \times \mathbf{\vec w})\\ =\begin{vmatrix} u_x&u_y&u_z\\ v_x&v_y&v_z\\ w_x&w_y&w_z \end{vmatrix} =\begin{vmatrix} u_x&v_x&w_x\\ u_y&v_y&w_y\\ u_z&v_z&w_z\end{vmatrix} \] 其物理意义为： \(\mathbf{\vec u} ,\mathbf{\vec v} ,\mathbf{\vec w}\) 为三个棱边所围成的平行六面体的体积。 \(\mathbf{\vec u} ,\mathbf{\vec v} ,\mathbf{\vec w}\) 构成右手系时，该平行六面体的体积为正号。

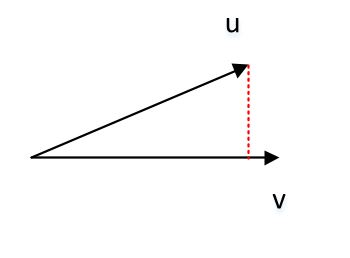
6. 两个向量的并矢：给定两个向 \(\mathbf {\vec x}=(x_1,x_2,\cdots,x_n)^{T}, \mathbf {\vec y}= (y_1,y_2,\cdots,y_m)^{T}\) ，则向量的并矢记作：
   \[\mathbf {\vec x}\mathbf {\vec y} =\begin{bmatrix}x_1y_1&x_1y_2&\cdots&x_1y_m\\ x_2y_1&x_2y_2&\cdots&x_2y_m\\ \vdots&\vdots&\ddots&\vdots\\ x_ny_1&x_ny_2&\cdots&x_ny_m\\ \end{bmatrix}\] 也记 \(\mathbf {\vec x}\otimes\mathbf {\vec y}\) 或 \(\mathbf {\vec x} \mathbf {\vec y}^{T}\) 。

三、矩阵运算

1. 给定两个矩 \(\mathbf A=(a_{i,j}) \in \mathbb R^{m\times n},\mathbf B=(b_{i,j}) \in \mathbb R^{m\times n}\) ，定义：
   • 阿达马积Hadamard product（又称作逐元素积）：
     \[\mathbf A \circ \mathbf B =\begin{bmatrix} a_{1,1}b_{1,1}&a_{1,2}b_{1,2}&\cdots&a_{1,n}b_{1,n}\\ a_{2,1}b_{2,1}&a_{2,2}b_{2,2}&\cdots&a_{2,n}b_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{m,1}b_{m,1}&a_{m,2}b_{m,2}&\cdots&a_{m,n}b_{m,n}\end{bmatrix}\]
   • 克罗内积Kronnecker product：
     \[\mathbf A \otimes \mathbf B =\begin{bmatrix}a_{1,1}\mathbf B&a_{1,2}\mathbf B&\cdots&a_{1,n}\mathbf B\\ a_{2,1}\mathbf B&a_{2,2}\mathbf B&\cdots&a_{2,n}\mathbf B\\ \vdots&\vdots&\ddots&\vdots\\ a_{m,1}\mathbf B&a_{m,2}\mathbf B&\cdots&a_{m,n}\mathbf B \end{bmatrix}\]

2. \(\mathbf {\vec x},\mathbf {\vec a},\mathbf {\vec b},\mathbf {\vec c}\) \(n\) 阶向量 \(\mathbf A,\mathbf B,\mathbf C,\mathbf X\) \(n\) 阶方阵，则有：
   \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf {\vec x}) }{\partial \mathbf {\vec x} }=\frac{\partial(\mathbf {\vec x}^{T}\mathbf {\vec a}) }{\partial \mathbf {\vec x} } =\mathbf {\vec a}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X\mathbf {\vec b}) }{\partial \mathbf X }=\mathbf {\vec a}\mathbf {\vec b}^{T}=\mathbf {\vec a}\otimes\mathbf {\vec b}\in \mathbb R^{n\times n}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X^{T}\mathbf {\vec b}) }{\partial \mathbf X }=\mathbf {\vec b}\mathbf {\vec a}^{T}=\mathbf {\vec b}\otimes\mathbf {\vec a}\in \mathbb R^{n\times n}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X\mathbf {\vec a}) }{\partial \mathbf X }=\frac{\partial(\mathbf {\vec a}^{T}\mathbf X^{T}\mathbf {\vec a}) }{\partial \mathbf X }=\mathbf {\vec a}\otimes\mathbf {\vec a}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X^{T}\mathbf X\mathbf {\vec b}) }{\partial \mathbf X }=\mathbf X(\mathbf {\vec a}\otimes\mathbf {\vec b}+\mathbf {\vec b}\otimes\mathbf {\vec a})\] \[\frac{\partial[(\mathbf A\mathbf {\vec x}+\mathbf {\vec a})^{T}\mathbf C(\mathbf B\mathbf {\vec x}+\mathbf {\vec b})]}{\partial \mathbf {\vec x}}=\mathbf A^{T}\mathbf C(\mathbf B\mathbf {\vec x}+\mathbf {\vec b})+\mathbf B^{T}\mathbf C(\mathbf A\mathbf {\vec x}+\mathbf {\vec a})\] \[\frac{\partial (\mathbf {\vec x}^{T}\mathbf A \mathbf {\vec x})}{\partial \mathbf {\vec x}}=(\mathbf A+\mathbf A^{T})\mathbf {\vec x}\] \[\frac{\partial[(\mathbf X\mathbf {\vec b}+\mathbf {\vec c})^{T}\mathbf A(\mathbf X\mathbf {\vec b}+\mathbf {\vec c})]}{\partial \mathbf X}=(\mathbf A+\mathbf A^{T})(\mathbf X\mathbf {\vec b}+\mathbf {\vec c})\mathbf {\vec b}^{T} \] \[\frac{\partial (\mathbf {\vec b}^{T}\mathbf X^{T}\mathbf A \mathbf X\mathbf {\vec c})}{\partial \mathbf X}=\mathbf A^{T}\mathbf X\mathbf {\vec b}\mathbf {\vec c}^{T}+\mathbf A\mathbf X\mathbf {\vec c}\mathbf {\vec b}^{T}\]

3. 如 \(f\) 是一元函数，则：
   • 其逐元向量函数为 \(f(\mathbf{\vec x}) =(f(x_1),f(x_2),\cdots,f(x_n))^{T}\) 。
   • 其逐矩阵函数为：
     \[f(\mathbf X)=\begin{bmatrix} f(x_{1,1})&f(x_{1,2})&\cdots&f(x_{1,n})\f(x_{2,1})&f(x_{2,2})&\cdots&f(x_{2,n})\\vdots&\vdots&\ddots&\vdots\f(x_{m,1})&f(x_{m,2})&\cdots&f(x_{m,n})\\end{bmatrix}\]
   • 其逐元导数分别为：
     \[f^{\prime}(\mathbf{\vec x}) =(f^{\prime}(x1),f^{\prime}(x2),\cdots,f^{\prime}(x_n))^{T}\f^{\prime}(\mathbf X)=\begin{bmatrix} f^{\prime}(x_{1,1})&f^{\prime}(x_{1,2})&\cdots&f^{\prime}(x_{1,n})\f^{\prime}(x_{2,1})&f^{\prime}(x_{2,2})&\cdots&f^{\prime}(x_{2,n})\\vdots&\vdots&\ddots&\vdots\f^{\prime}(x_{m,1})&f^{\prime}(x_{m,2})&\cdots&f^{\prime}(x_{m,n})\\end{bmatrix}\]
4. 各种类型的偏导数：
   • 标量对标量的偏导数 \(\frac{\partial u}{\partial v}\) 。
   • 标量对向量 \(n\) 维向量）的偏导数 \(\frac{\partial u}{\partial \mathbf {\vec v}}=(\frac{\partial u}{\partial v_1},\frac{\partial u}{\partial v_2},\cdots,\frac{\partial u}{\partial v_n})^{T}\) 。
   • 标量对矩阵 \(m\times n\) 阶矩阵)的偏导数：
     \[\frac{\partial u}{\partial \mathbf V}=\begin{bmatrix} \frac{\partial u}{\partial V_{1,1}}&\frac{\partial u}{\partial V_{1,2}}&\cdots&\frac{\partial u}{\partial V_{1,n}}\\ \frac{\partial u}{\partial V_{2,1}}&\frac{\partial u}{\partial V_{2,2}}&\cdots&\frac{\partial u}{\partial V_{2,n}}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial u}{\partial V_{m,1}}&\frac{\partial u}{\partial V_{m,2}}&\cdots&\frac{\partial u}{\partial V_{m,n}} \end{bmatrix}\]
   • 向量 \(m\) 维向量）对标量的偏导数 \(\frac{\partial \mathbf {\vec u}}{\partial v}=(\frac{\partial u_1}{\partial v},\frac{\partial u_2}{\partial v},\cdots,\frac{\partial u_m}{\partial v})^{T}\) 。
   • 向量 \(m\) 维向量）对向量 \(n\) 维向量)的偏导数（雅可比矩阵，行优先）
     \[\frac{\partial \mathbf {\vec u}}{\partial \mathbf {\vec v}}=\begin{bmatrix} \frac{\partial u_1}{\partial v_1}&\frac{\partial u_1}{\partial v_2}&\cdots&\frac{\partial u_1}{\partial v_n}\\ \frac{\partial u_2}{\partial v_1}&\frac{\partial u_2}{\partial v_2}&\cdots&\frac{\partial u_2}{\partial v_n}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial u_m}{\partial v_1}&\frac{\partial u_m}{\partial v_2}&\cdots&\frac{\partial u_m}{\partial v_n} \end{bmatrix}\] 如果为列优先，则为上面矩阵的转置。
   • 矩阵 \(m\times n\) 阶矩阵)对标量的偏导数
     \[\frac{\partial \mathbf U}{\partial v}=\begin{bmatrix} \frac{\partial U_{1,1}}{\partial v}&\frac{\partial U_{1,2}}{\partial v}&\cdots&\frac{\partial U_{1,n}}{\partial v}\\ \frac{\partial U_{2,1}}{\partial v}&\frac{\partial U_{2,2}}{\partial v}&\cdots&\frac{\partial U_{2,n}}{\partial v}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial U_{m,1}}{\partial v}&\frac{\partial U_{m,2}}{\partial v}&\cdots&\frac{\partial U_{m,n}}{\partial v} \end{bmatrix}\]
5. 对于矩阵的迹，有下列偏导数成立：
   \[\frac{\partial [tr(f(\mathbf X))]}{\partial \mathbf X }=(f^{\prime}(\mathbf X))^{T}\] \[\frac{\partial [tr(\mathbf A\mathbf X\mathbf B)]}{\partial \mathbf X }=\mathbf A^{T}\mathbf B^{T} \] \[\frac{\partial [tr(\mathbf A\mathbf X^{T}\mathbf B)]}{\partial \mathbf X }=\mathbf B\mathbf A \] \[\frac{\partial [tr(\mathbf A\otimes\mathbf X )]}{\partial \mathbf X }=tr(\mathbf A)\mathbf I\] \[\frac{\partial [tr(\mathbf A\mathbf X \mathbf B\mathbf X)]}{\partial \mathbf X }=\mathbf A^{T}\mathbf X^{T}\mathbf B^{T}+\mathbf B^{T}\mathbf X \mathbf A^{T} \] \[\frac{\partial [tr(\mathbf X^{T} \mathbf B\mathbf X \mathbf C)]}{\partial \mathbf X }=(\mathbf B^{T}+\mathbf B)\mathbf X \mathbf C \mathbf C^{T} \] \[\frac{\partial [tr(\mathbf C^{T}\mathbf X^{T} \mathbf B\mathbf X \mathbf C)]}{\partial \mathbf X }=\mathbf B\mathbf X \mathbf C +\mathbf B^{T}\mathbf X \mathbf C^{T} \] \[\frac{\partial [tr(\mathbf A\mathbf X \mathbf B\mathbf X^{T} \mathbf C)]}{\partial \mathbf X }= \mathbf A^{T}\mathbf C^{T}\mathbf X\mathbf B^{T}+\mathbf C \mathbf A \mathbf X \mathbf B\] \[\frac{\partial [tr((\mathbf A\mathbf X\mathbf B+\mathbf C)(\mathbf A\mathbf X\mathbf B+\mathbf C))]}{\partial \mathbf X }= 2\mathbf A ^{T}(\mathbf A\mathbf X\mathbf B+\mathbf C)\mathbf B^{T}\]

6. 假 \(\mathbf U= f(\mathbf X)\) 是关 \(\mathbf X\) 的矩阵值函数 \(f:\mathbb R^{m\times n}\rightarrow \mathbb R^{m\times n}\) ）， \(g(\mathbf U)\) 是关 \(\mathbf U\) 的实值函数 $g:\mathbb R^{m\times n}\rightarrow \mathbb R $ ），则下面链式法则成立：
   \[\frac{\partial g(\mathbf U)}{\partial \mathbf X}= \left(\frac{\partial g(\mathbf U)}{\partial x_{i,j}}\right)_{m\times n}=\begin{bmatrix} \frac{\partial g(\mathbf U)}{\partial x_{1,1}}&\frac{\partial g(\mathbf U)}{\partial x_{1,2}}&\cdots&\frac{\partial g(\mathbf U)}{\partial x_{1,n}}\\ \frac{\partial g(\mathbf U)}{\partial x_{2,1}}&\frac{\partial g(\mathbf U)}{\partial x_{2,2}}&\cdots&\frac{\partial g(\mathbf U)}{\partial x_{2,n}}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial g(\mathbf U)}{\partial x_{m,1}}&\frac{\partial g(\mathbf U)}{\partial x_{m,2}}&\cdots&\frac{\partial g(\mathbf U)}{\partial x_{m,n}}\\ \end{bmatrix}\\ =\left(\sum_{k}\sum_{l}\frac{\partial g(\mathbf U)}{\partial u_{k,l}}\frac{\partial u_{k,l}}{\partial x_{i,j}}\right)_{m\times n}=\left(tr\left[\left(\frac{\partial g(\mathbf U)}{\partial \mathbf U}\right)^{T}\frac{\partial \mathbf U}{\partial x_{i,j}}\right]\right)_{m\times n}\]

?

本文转载自华校专老师博客，博客地址：http://www.huaxiaozhuan.com/

【机器学习数学基础】线性代数基础

标签：center   mes   display   种类型   end   图片   play   数学基础   方向   

原文地址：https://www.cnblogs.com/guoyaohua/p/9803027.html