降维——PCA主成分分析

标签：find   逻辑   获得   check   margin   http   错误   info   style   

运用二维降维到一维的例子帮助理解

对于如下二维数据

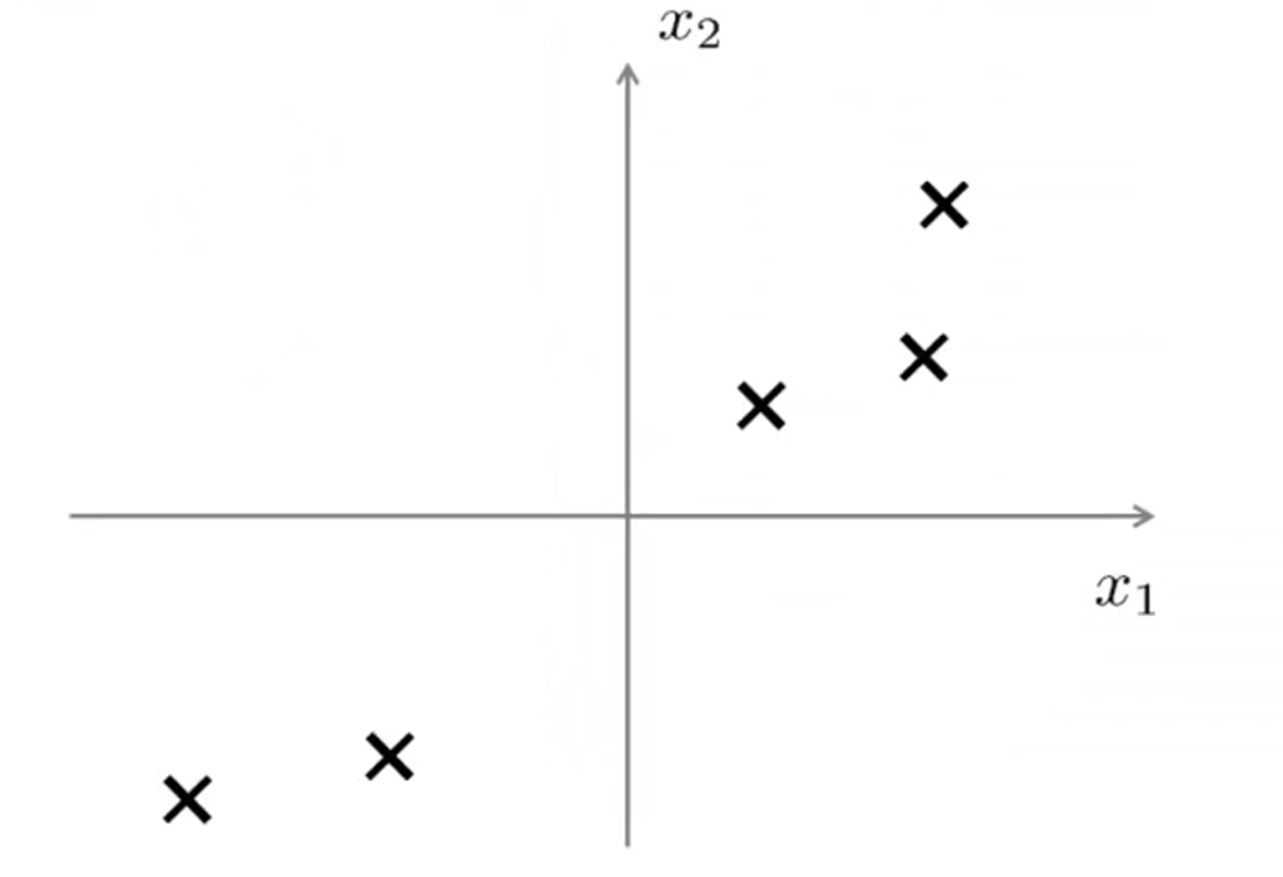
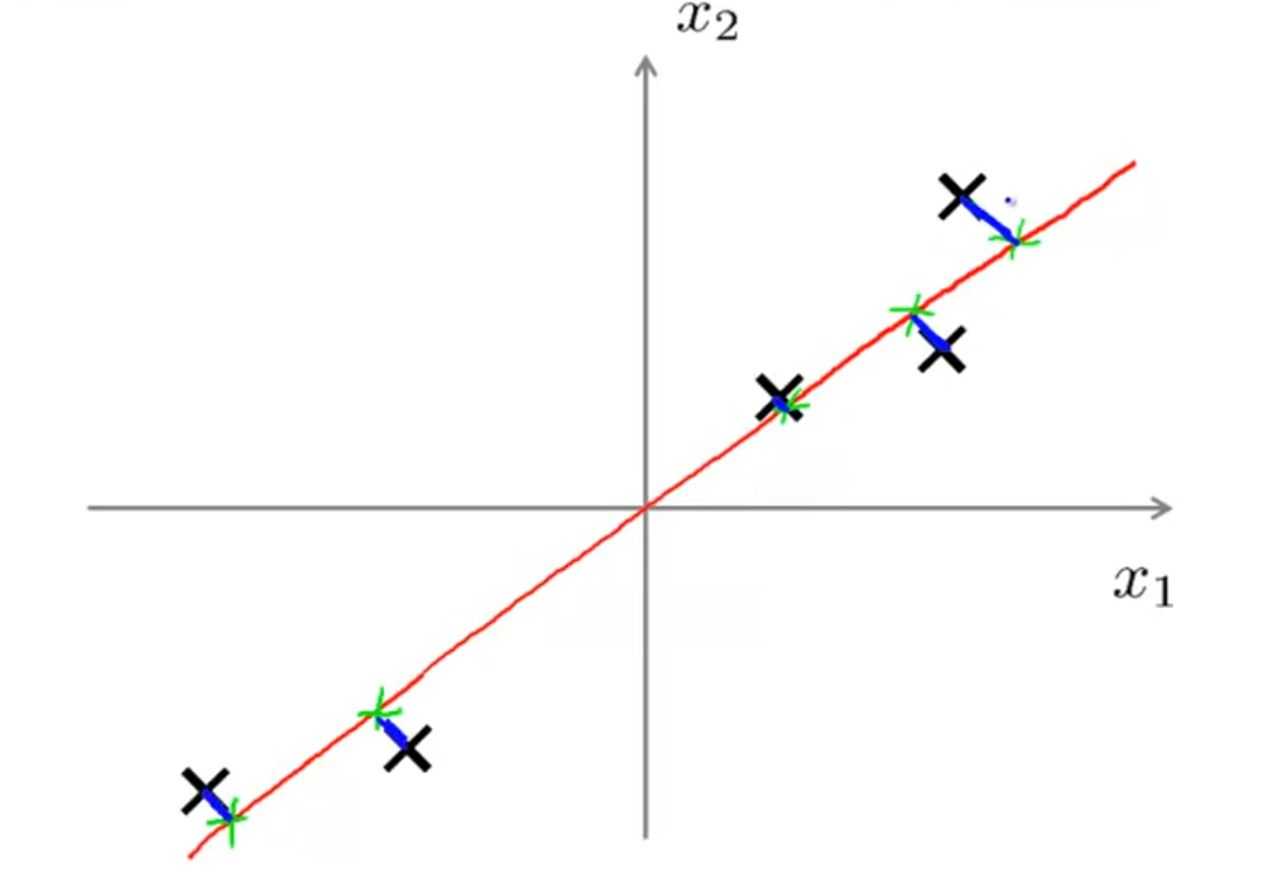
PCA算法会试图寻找一条直线使得所有数据到这个直线的距离的平方和最小（”投影误差“最小）（图中所有蓝色线长度的平方和）（注意：做PCA之前需要将数据进行标准化，将数据映射到（0，1）区间内）

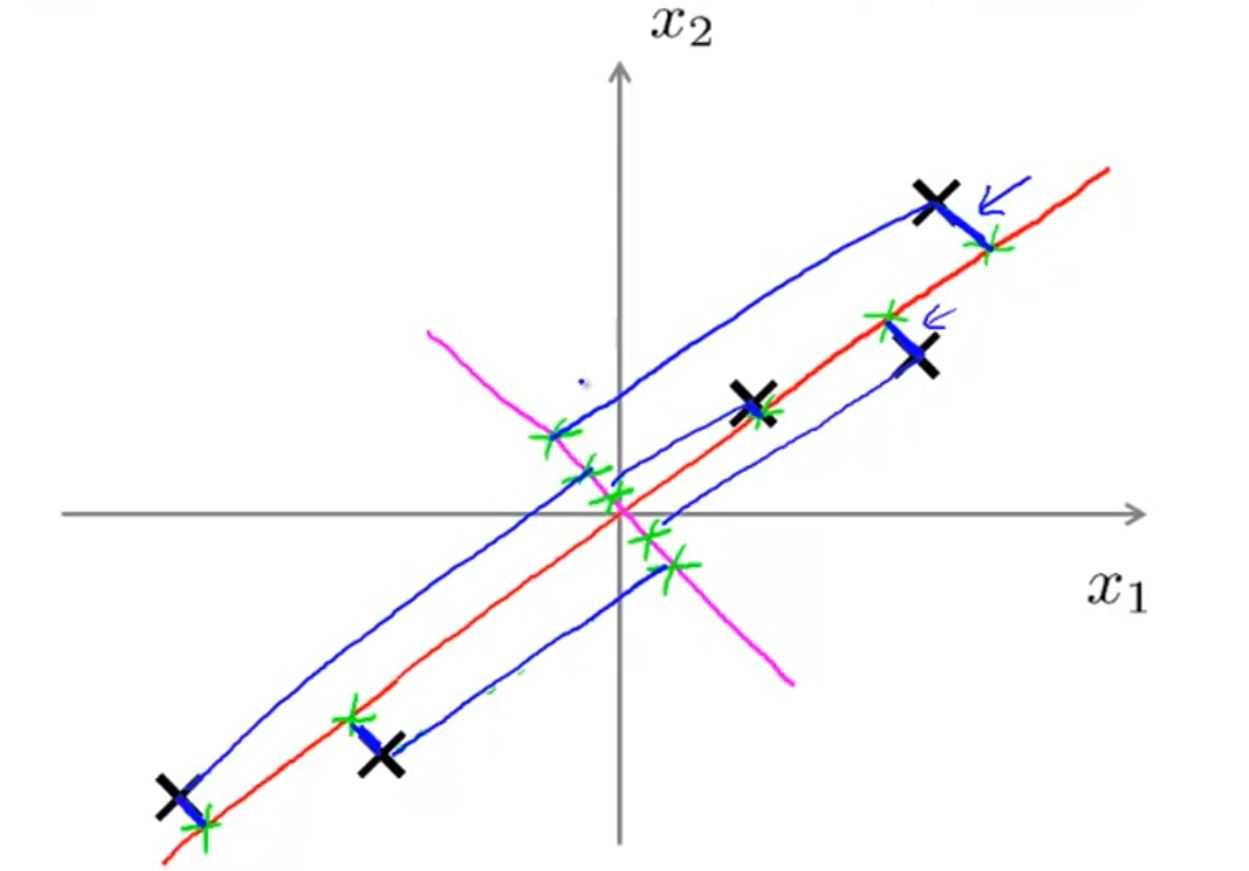
对于以下两种情况，PCA会选择红色线

更书面的表达

Reduce from 2-dimension to 1-dimension: Find a direction (a vector u⁽¹⁾) onto which to project the data so as to minimize the projection error.

对于将二维数据降维到一维，PCA试图寻找一个向量使得所有数据投影到这个向量上后有最小的”投影误差“

Reduce from n-dimension to k-dimension: Find k vectors u⁽¹⁾, u⁽²⁾,..., u^(k) onto which to project the data, so as to minimize the projection error.

从n维减小到k维：找到投影数据的k个向量u⁽¹⁾, u⁽²⁾,..., u^(k)，以便最小化投影误差。

PCA不是线性回归！

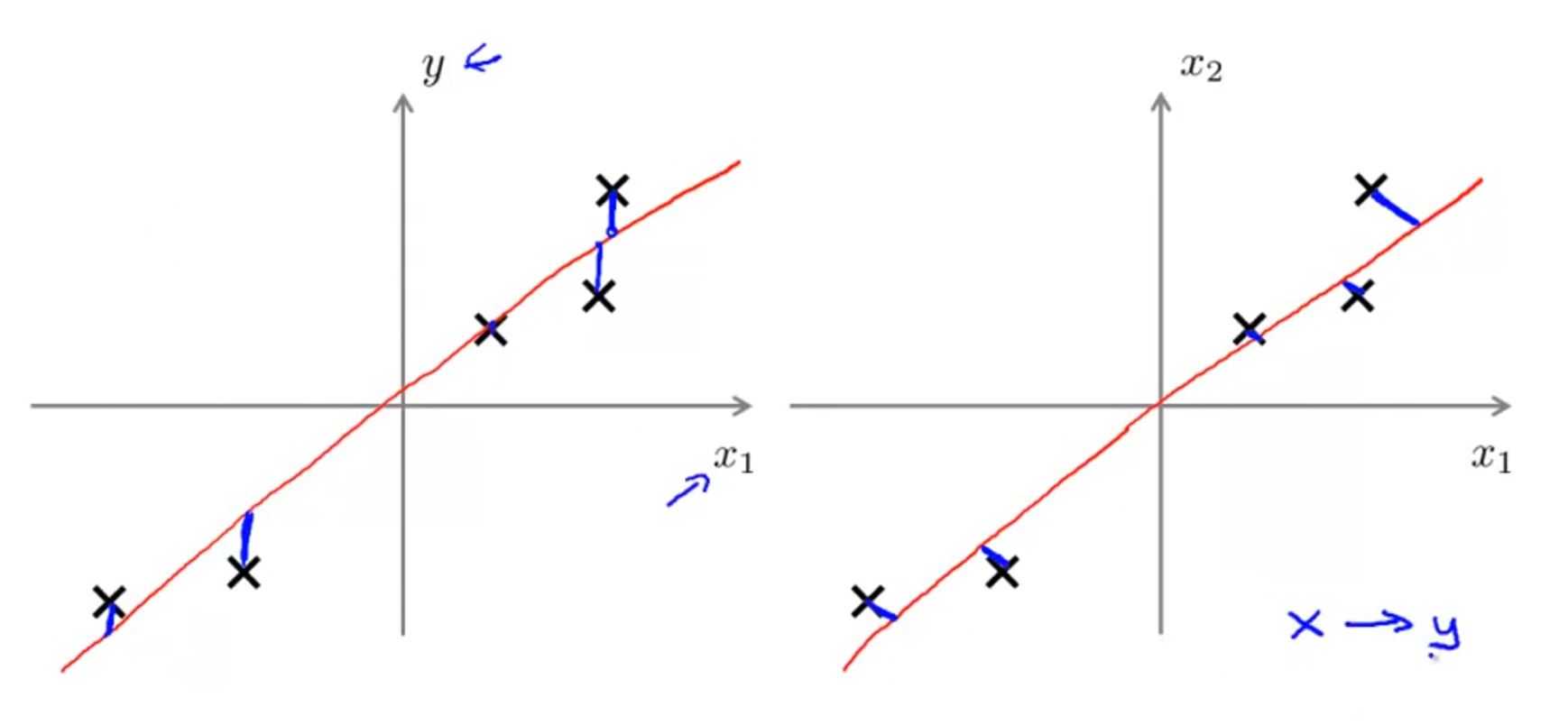
这两个图可能有些相似，其实有很大差异

• 线性回归需要根据x计算y，而PCA不需要
• 线性回归计算的是预测值y_pre与y的差，而PCA计算的是”投影误差“

可以看到，PCA需要计算两个量：k个向量u⁽¹⁾, u⁽²⁾,..., u^(k)；投影误差。

记

\[{U_{reduce}} = \left[ {\begin{array}{*{20}{c}}
{}\\
{{u^{\left( 1 \right)}}}\\
{}
\end{array}\begin{array}{*{20}{c}}
{}\\
{{u^{\left( 2 \right)}}}\\
{}
\end{array}\begin{array}{*{20}{c}}
{}\\
{...}\\
{}
\end{array}\begin{array}{*{20}{c}}
{}\\
{{u^{\left( k \right)}}}\\
{}
\end{array}} \right]\]

因为原始数据 x 是 n x 1 的向量，投影后的 z 是 k x 1。所以 U_reduce 是 n x k 矩阵

 记

\[\begin{array}{l}
{z^{\left( i \right)}} = {U_{reduce}}^T{x^{\left( i \right)}}\\
x_{approx}^{\left( i \right)} = {U_{reduce}}{z^{\left( i \right)}}
\end{array}\]

如何选择 k （主成分的数量）

记”平均投影误差“

\[{\frac{1}{m}{{\sum\limits_{i = 1}^m {\left\| {{x^{\left( i \right)}} - x_{approx}^{\left( i \right)}} \right\|} }^2}}\]

记”total variation in the data“

\[{\frac{1}{m}\sum\limits_{i = 1}^m {{{\left\| {{x^{\left( i \right)}}} \right\|}^2}} }\]

则，PCA会选择最小的 k 使得

\[\frac{{\frac{1}{m}{{\sum\limits_{i = 1}^m {\left\| {{x^{\left( i \right)}} - x_{approx}^{\left( i \right)}} \right\|} }^2}}}{{\frac{1}{m}\sum\limits_{i = 1}^m {{{\left\| {{x^{\left( i \right)}}} \right\|}^2}} }} \le 0.01\]

可以理解为降维后的数据要能代表原数据 99% 的”信息“。（通常取 95%-99%）

 选择 k 的具体步骤：

Try PCA with k = 1

compute 

\[{U_{reduce}}\]

\[{z^{\left( i \right)}}\]

\[x_{approx}^{\left( i \right)}\]

check if

\[\frac{{\frac{1}{m}{{\sum\limits_{i = 1}^m {\left\| {{x^{\left( i \right)}} - x_{approx}^{\left( i \right)}} \right\|} }^2}}}{{\frac{1}{m}\sum\limits_{i = 1}^m {{{\left\| {{x^{\left( i \right)}}} \right\|}^2}} }} \le 0.01?\]

increase k, back to upper.

运用PCA的建议

只在训练集上”运行“PCA，然后将得到的”映射关系“”应用“到交叉验证集和测试集上。

错误运用PCA的例子——运用PCA防止过拟合

比如将 1000 维的 x 降维到 100 维的 z，这也许能正常工作，但是这是一个不好的例子。

正确的避免过拟合的例子是正则化。

一般情况下一个标准的”机器学习系统“的设计如下：

• 获得数据
• 运行PCA
• 运行逻辑回归
• 在交叉验证集和测试集上运行

但是，建议是先不进行PCA而使用原始数据进行研究，只有当没有PCA达不到你想要的效果时在考虑使用PCA。

降维——PCA主成分分析

标签：find   逻辑   获得   check   margin   http   错误   info   style   

原文地址：https://www.cnblogs.com/qkloveslife/p/9903582.html