1. 欠拟合与过拟合概念

标签：tree   red   方式   mit   直线   数学   参与   微软   回归   

1. 欠拟合与过拟合概念
   1. 欠拟合与过拟合概念

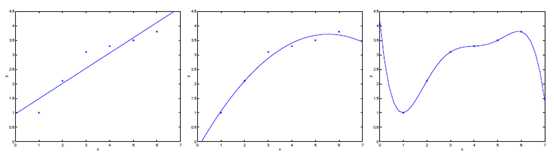
图3-1 欠拟合与过拟合概念演示

通常，你选择让交给学习算法处理的特征的方式对算法的工作过程有很大影响。如图3-1中左图所示，采用了y = θ₀ + θ₁x的假设来建立模型，我们发现较少的特征并不能很好的拟合数据，这种情况称之为欠拟合(underfitting)。而如果我们采用了y = θ₀ + θ₁x+ θ₂x₂的假设来建立模型，发现能够非常好的拟合数据(如中图所示)；此外，如果我们采用了y = θ₀ + θ₁x+ θ₂x₂+ θ₃x₃ + θ₄x₄ + θ₅x₅，发现较多的特征导致了所有的训练数据都被完美的拟合上了，这种情况称之为过拟合(overfitting)。

这里，我们稍微谈一下过拟合问题，过拟合的标准定义(来自Mitchell的机器学习)标准定义：给定一个假设空间H，一个假设h属于H，如果存在其他的假设h‘属于H,使得在训练样例上h的错误率比h‘小，但在整个实例分布上h‘比h的错误率小，那么就说假设h过度拟合训练数据。过拟合问题往往是由于训练数据少(无法覆盖所有的特征学习，换句话也可以认为是特征太多)等原因造成的。在以后的课程会具体讲解。

对于此类学习问题，一般使用特征选择算法(有一讲专门讲)或非参数学习算法，下面将要降到的局部加权线性回归就是属于该方法，以此缓解对于特征选取的需求。

1. 局部加权线性回归

局部加权线性回归(locally weighted linear regression)属于非参数学习算法的一种，也称作Loess。

对于原始的回归分析，我们基本的算法思想是：

1) 寻找合适的θ使得 最小；2) 预测输出。

而对于局部加权线性回归算法的基本思想是：

1) 寻找合适的θ使得 最小；2) 预测输出。

这里，局部加权线性回归与原始回归分析不同在于，多了权重w_i，该值是正的。对于特点的点，如果权重w较大，那么我们选择合适的θ使得最小；如果权重w较小，那么误差的平方方在拟合过程中将会被忽略掉。换言之，对于局部加权回归，当要处理x时，会检查数据集合，并且只考虑位于x周围的固定区域内的数据点(较远点不影响因权重较低而被忽略)，对这个区域内的点做线性回归，拟合出一条直线，根据这条拟合直线对x的输出，作为算法返回的结果。

一个标准的且常用的权重选择如下：

w_i = exp(-)

需要注意，这里的x是我们要预测的输入，而x_i是训练样本数据。从公式看，离x越近的点，权重越大，而这里的权重公式虽然与高斯分布很像，但是没有任何关系，当然用户可以选择不同的函数作为权重函数。而τ决定了各个点权重随距离下降的速度，称之为波长。τ越大，即波长越大，权重下降速度越慢。如何选择合适的τ值，将会在模型选择一讲讲述。另外需要注意的是，如果x是多维特征数据的时候，那么权重是多维特征参与计算后的结果(结果为一维)，即w(i) = exp(?(x(i)?x)^T (x(i)?x)/())。(i表示样本下标，j表示特征下标)

参数学习算法(parametric learning algorithm)定义：参数学习算法是一类有固定数目参数，以用来进行数据拟合的算法。设该固定的参数集合为。线性回归即使参数学习算法的一个例子。非参数学习算法(Non-parametric learning algorithm)定义：一个参数数量会随m(训练集大小)增长的算法。通常定义为参数数量虽m线性增长。换句话说，就是算法所需要的东西会随着训练集合线性增长，算法的维持是基于整个训练集合的，即使是在学习以后。

由于每次进行预测都要根据训练集拟合曲线，如果训练样本非常大，那么该方法可能是代价较大，可以参考Andrew Moore的KD-tree方法来思考解决。此外，局部加权线性回归依旧无法避免欠拟合和过拟合的问题。

1. 回归模型的概率解释

对于回归问题，我们不禁要问为什么线性回归或者说为什么最小均方法是一个合理的选择呢？这里我们通过一系列的概率假设给出一个解释。

首先，我们假设预测值y与输入变量满足如下方程：

y(i) = θ^T*x(i) + ε(i)

其中ε(i)表示由于各种未考虑的因素造成的残差或者噪音等，我们进一步假设ε(i)独立同分布(误差项彼此之间是独立的，并且他们服从均值和方差相同的高斯分布)，服从均值为0，方差为δ²的正态分布，即ε(i) ～(0, δ²)，(为什么如此假设呢？一个是便于数学计算，另一个是可以通过中心极限定理等证明该残差服从正态分布)具体表示为：

p(ε(i)) =

代入之后如下：

p(y(i)|x(i); θ) =

这里的θ不是随机变量，而是具体的值。p(y(i)|x(i); θ)，表示对于给定的x(i)和θ，y(i)出现的概率。那么对于一组y的话，可以表示为p(|X; θ)，这就相当于θ的似然性。(注意似然性与概率性不同，概率用于在已知一些参数的情况下，预测接下来的观测所得到的结果，而似然性则是用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。那么参数θ的似然函数如下：

L(θ) = L(θ;X, ) = p(|X; θ)

根据以上的假设和分析，我们得到：

L(θ)     =

        =

对于该似然函数，我们已知了x,y，需要找一个合适且合理的方法求取θ。最大似然法则告诉我们选择的θ应该是L(θ)最大。实际意义，选择参数使数据出现的可能性尽可能的大(让发生的事情概率最大化)。为了方便计算，我们通常对似然函数求取对数，将乘机项转化成求和。化简如下(注意本文中log的含义表示取自然对数，而不是取10为底对数)：

?(θ)     = log(L(θ))

        = log()

        =

        =m*log() -

对于上式，最大化似然函数L(θ)就相当于最小化，即J(θ)。

总结而言，对于数据作出概率假设之后，最小二乘回归方法相当于最大化θ的似然函数。通过概率假设，我们验证该方法的合理性，然而这些概率假设对于最小二乘法的合理性却并不是必要的，当然确实有其他的更自然的假设能够证明最小二乘法的合理性。

需要注意的是，对于上面的讨论，最终的θ选择并不依赖于(我们假设的误差俯冲的分布方差)尽管值并不知道。当讨论到指数族和广义线性回归的时候，我们还会提到这些。

注意：我们用到的假设，第一残差项独立同分布且分布均值为0，样本之间相互独立，此外，要想有结果需要输入特征不存在多重共线性，即输入特征是满秩矩阵。

1. Logistic回归模型

在以上的讨论中，主要是关于回归问题。借来下，我们讨论分类问题，与回归问题很类似，不过待预测的y不是连续变量，而是有限的离散变量。这里，我们主要讨论二元分类，即预测的结果只有是否或者对错之类，习惯用01表示，其中0表示否定(negative)的结果，1表示肯定(positive)的结果。对于给定的输入X，y也被称之为标签(label)。

针对分类问题，我们可以暂时忽略y的离散性，而采用回归分析的方法进行分析。然而，我们很容易发现回归分析效果很差，尤其是不好解释预测值不等于{0,1}的情况。为此，我们需要更改我们假设：

h_θ(x) = g() = 这里的g(z) = ，被称之为logistic函数或sigmoid函数。函数图形如下：

当z趋近于无穷大的时候，g(z)趋近于1，当z趋近于无穷小的时候，g(z)趋近于0。这里需要注意的是：我们仍然设定截距x0=1,即 = θ₀ + 。此外，对于g(z)的导数g‘ (z) : g‘(z) = g(z)*(1-g(z))。因此，对于使用logistic函数作为假设H的模型，我们同样采用假设和使用最小二乘法来最大化参数的最大似然函数。

我们假设：P(y=1 | x;θ) = h_θ(x) P(y=0 | x;θ) = 1- h_θ(x) 该假设可以归结为：

    p(y | x;θ) = (h_θ(x))^y* (1- h_θ(x))^(1-y)

那么最大似然函数如下：

取对数优化后：

同样，我们采用梯度下降法来迭代求取参数值，即按照θ_j := θ_j? α*方式跟新参数值。

在推导过程中，我们使用g‘(z)=g(z)*(1-g(z))该特性。最终的更新结果如下：

对比LMS算法中更新参数的方法，与logistic回归法更新权重的一样。唯一不同的在于假设h_θ(x)，这个时候的假设是非线性的。当我们将到广义线性回归的时候，我们再来看是不是所有的算法够可以归结到这样的更新方式呢？

1. 感知器学习模型

在logistic方法中，g(z)会生成[0,1]之间的小数，但如何是g(z)只生成0或1？这里我们重新定义g(z)函数如下：

之后，我们同样假设h_θ(x) = g() ，按照之前的方法(梯度下降法)我们将会同样得到参数更新的方式为：θ_j := θ_j + α(y-h(xⁱ))*x_jⁱ ，该模型称之为感知器学习算法(perceptron learning algorithm)。

20世纪60年代，认为在神经网络模型采用"感知器学习"算法的神经元是较为粗糙的，但是他仍然能很好的表达学习算法理论。虽然从公式外形上来看，感知器学习与logistic回归和线性回归差不多，但是我们很难赋予感知器预测值的概率解释，或者使用最大似然估计推导出感知器模型。

1. 欠拟合与过拟合概念

标签：tree   red   方式   mit   直线   数学   参与   微软   回归   

原文地址：https://www.cnblogs.com/kexinxin/p/9904392.html