标签:poi psc ilo VID 特性 特征 最优 系统 最优化问题
目录
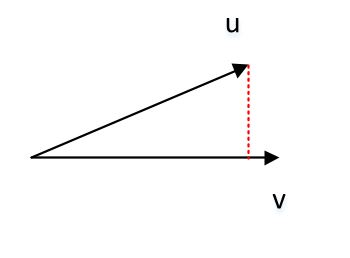
F范数:设矩 \(\mathbf A=(a_{i,j})_{m\times n}\) ,则其F范数为 \(||\mathbf A||_F=\sqrt{\sum_{i,j}a_{i,j}^{2}}\) 。F 范数等 \(\mathbf A\mathbf A^T\) 的迹的平方根 \(||\mathbf A||_F=\sqrt{tr(\mathbf A \mathbf A^{T})}\) 。三维向量的点积 \(\mathbf{\vec u}\cdot\mathbf{\vec v} =u _xv_x+u_yv_y+u_zv_z = |\mathbf{\vec u}| | \mathbf{\vec v}| \cos(\mathbf{\vec u},\mathbf{\vec v})\) 。
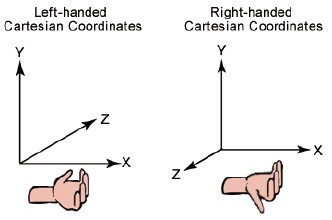
两个向量的并矢:给定两个向 \(\mathbf {\vec x}=(x_1,x_2,\cdots,x_n)^{T}, \mathbf {\vec y}= (y_1,y_2,\cdots,y_m)^{T}\) ,则向量的并矢记作:
\[\mathbf {\vec x}\mathbf {\vec y} =\begin{bmatrix}x_1y_1&x_1y_2&\cdots&x_1y_m\\ x_2y_1&x_2y_2&\cdots&x_2y_m\\ \vdots&\vdots&\ddots&\vdots\\ x_ny_1&x_ny_2&\cdots&x_ny_m\\ \end{bmatrix}\] 也记 \(\mathbf {\vec x}\otimes\mathbf {\vec y}\) 或 \(\mathbf {\vec x} \mathbf {\vec y}^{T}\) 。
Hadamard product(又称作逐元素积):Kronnecker product:\(\mathbf {\vec x},\mathbf {\vec a},\mathbf {\vec b},\mathbf {\vec c}\) \(n\) 阶向量 \(\mathbf A,\mathbf B,\mathbf C,\mathbf X\) \(n\) 阶方阵,则有:
\[\frac{\partial(\mathbf {\vec a}^{T}\mathbf {\vec x}) }{\partial \mathbf {\vec x} }=\frac{\partial(\mathbf {\vec x}^{T}\mathbf {\vec a}) }{\partial \mathbf {\vec x} } =\mathbf {\vec a}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X\mathbf {\vec b}) }{\partial \mathbf X }=\mathbf {\vec a}\mathbf {\vec b}^{T}=\mathbf {\vec a}\otimes\mathbf {\vec b}\in \mathbb R^{n\times n}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X^{T}\mathbf {\vec b}) }{\partial \mathbf X }=\mathbf {\vec b}\mathbf {\vec a}^{T}=\mathbf {\vec b}\otimes\mathbf {\vec a}\in \mathbb R^{n\times n}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X\mathbf {\vec a}) }{\partial \mathbf X }=\frac{\partial(\mathbf {\vec a}^{T}\mathbf X^{T}\mathbf {\vec a}) }{\partial \mathbf X }=\mathbf {\vec a}\otimes\mathbf {\vec a}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X^{T}\mathbf X\mathbf {\vec b}) }{\partial \mathbf X }=\mathbf X(\mathbf {\vec a}\otimes\mathbf {\vec b}+\mathbf {\vec b}\otimes\mathbf {\vec a})\] \[\frac{\partial[(\mathbf A\mathbf {\vec x}+\mathbf {\vec a})^{T}\mathbf C(\mathbf B\mathbf {\vec x}+\mathbf {\vec b})]}{\partial \mathbf {\vec x}}=\mathbf A^{T}\mathbf C(\mathbf B\mathbf {\vec x}+\mathbf {\vec b})+\mathbf B^{T}\mathbf C(\mathbf A\mathbf {\vec x}+\mathbf {\vec a})\] \[\frac{\partial (\mathbf {\vec x}^{T}\mathbf A \mathbf {\vec x})}{\partial \mathbf {\vec x}}=(\mathbf A+\mathbf A^{T})\mathbf {\vec x}\] \[\frac{\partial[(\mathbf X\mathbf {\vec b}+\mathbf {\vec c})^{T}\mathbf A(\mathbf X\mathbf {\vec b}+\mathbf {\vec c})]}{\partial \mathbf X}=(\mathbf A+\mathbf A^{T})(\mathbf X\mathbf {\vec b}+\mathbf {\vec c})\mathbf {\vec b}^{T} \] \[\frac{\partial (\mathbf {\vec b}^{T}\mathbf X^{T}\mathbf A \mathbf X\mathbf {\vec c})}{\partial \mathbf X}=\mathbf A^{T}\mathbf X\mathbf {\vec b}\mathbf {\vec c}^{T}+\mathbf A\mathbf X\mathbf {\vec c}\mathbf {\vec b}^{T}\]
假 \(\mathbf U= f(\mathbf X)\) 是关 \(\mathbf X\) 的矩阵值函数 \(f:\mathbb R^{m\times n}\rightarrow \mathbb R^{m\times n}\) ), \(g(\mathbf U)\) 是关 \(\mathbf U\) 的实值函数 $g:\mathbb R^{m\times n}\rightarrow \mathbb R $ ),则下面链式法则成立:
\[\frac{\partial g(\mathbf U)}{\partial \mathbf X}=
\left(\frac{\partial g(\mathbf U)}{\partial x_{i,j}}\right)_{m\times n}=\begin{bmatrix}
\frac{\partial g(\mathbf U)}{\partial x_{1,1}}&\frac{\partial g(\mathbf U)}{\partial x_{1,2}}&\cdots&\frac{\partial g(\mathbf U)}{\partial x_{1,n}}\\
\frac{\partial g(\mathbf U)}{\partial x_{2,1}}&\frac{\partial g(\mathbf U)}{\partial x_{2,2}}&\cdots&\frac{\partial g(\mathbf U)}{\partial x_{2,n}}\\
\vdots&\vdots&\ddots&\vdots\\
\frac{\partial g(\mathbf U)}{\partial x_{m,1}}&\frac{\partial g(\mathbf U)}{\partial x_{m,2}}&\cdots&\frac{\partial g(\mathbf U)}{\partial x_{m,n}}\\
\end{bmatrix}\\
=\left(\sum_{k}\sum_{l}\frac{\partial g(\mathbf U)}{\partial u_{k,l}}\frac{\partial u_{k,l}}{\partial x_{i,j}}\right)_{m\times n}=\left(tr\left[\left(\frac{\partial g(\mathbf U)}{\partial \mathbf U}\right)^{T}\frac{\partial \mathbf U}{\partial x_{i,j}}\right]\right)_{m\times n}\]
条件概率:已 \(A\) 事件发生的条件 \(B\) 发生的概率,记 \(P(B\mid A)\) ,它等于事 \(AB\) 的概率相对于事 \(A\) 的概率,即:
\[P(B\mid A)=\frac {P(AB)}{P(A)}\] 其中必须 \(P(A) \gt 0\)
两个随机变 \(\mathbf x,\mathbf y\) 关于随机变 \(\mathbf z\) 条件独立的数学描述:
\[\forall x\in \mathcal X,\forall y\in \mathcal Y,\forall z \in\mathcal Z\P(\mathbf x=x,\mathbf y=y\mid \mathbf z=z)=P(\mathbf x=x\mid \mathbf z=z)P(\mathbf y=y\mid \mathbf z=z)\] 记作 \(\mathbf x \bot \mathbf y \mid \mathbf z\)
\({\mathbf x}\) 为连续型随机变量, \({\mathbf y}\) 的期望存在,则:
\[\mathbb E[{\mathbf y}]=\mathbb E[g({\mathbf x})]=\int_{-\infty}^{\infty}g(x)p(x)dx\] 该定理的意义在于:当 \(\mathbb E({\mathbf y})\) 时,不必计算 \({\mathbf y}\) 的分布,只需要利 \({\mathbf x}\) 的分布即可。该定理可以推广至两个或者两个以上随机变量的情况。此时:
\[ \mathbb E[Z]=\mathbb E[g({\mathbf x},{\mathbf y})]=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(x,y)p(x,y)dxdy\]
上述公式也记做:
\[\mathbb E_{\mathbf x\sim P}[g(x)]=\sum_{x}g(x)p(x)\\mathbb E_{\mathbf x\sim P}[g(x)]=\int g(x)p(x)dx\\mathbb E_{\mathbf x,\mathbf y\sim P}[g(x)]\int g(x,y)p(x,y)dxdy\]
\(|\rho_{{\mathbf x}{\mathbf y}}| = 1\) 的充要条件是,存在常数 \(a,b\) 使得 \(P\{{\mathbf y}=a+b{\mathbf x}\}=1\)
\(|\rho_{{\mathbf x}{\mathbf y}}|\) 较大时 \(e\) 较小,表明随机变 \({\mathbf x}\) \({\mathbf y}\) 联系较紧密,于 \(\rho_{{\mathbf x}{\mathbf y}}\) 是一个表 \({\mathbf x}\) \({\mathbf y}\) 之间线性关系紧密程度的量。
由于 \(c_{ij}=c_{ji}, i\ne j, i,j=1,2,\cdots,n\) 因此协方差矩阵是个对称阵
通 \(n\) 维随机变量的分布是不知道的,或者太复杂以致数学上不容易处理。因此实际中协方差矩阵非常重要。
切比雪夫不等式:随机变 \({\mathbf x}\) 具有期 \(\mathbb E[{\mathbf x}] =\mu\) ,方 \(Var({\mathbf x})=\sigma^{2}\) ,对于任意正 \(\varepsilon\) ,不等式
\[P\{|{\mathbf x}-\mu| \ge \varepsilon\} \le \frac {\sigma^{2}}{\varepsilon^{2}}\] 成立
其意义是:对于距 $\mathbb E[{\mathbf x}] $ 足够远的地方(距离大于等 \(\varepsilon\) ),事件出现的概率是小于等 $ \frac {\sigma^{2}}{\varepsilon^{2}}$ ;即事件出现在区 \([\mu-\varepsilon , \mu+\varepsilon]\) 的概率大 \(1- \frac {\sigma^{2}}{\varepsilon^{2}}\)
该不等式给出了随机变 \({\mathbf x}\) 在分布未知的情况下,事 \(\{|{\mathbf x}-\mu| \le \varepsilon\}\) 的下限估计( \(P\{|{\mathbf x}-\mu| \lt 3\sigma\} \ge 0.8889\)
证明:
\[P\{|{\mathbf x}-\mu| \ge \varepsilon\}=\int_{|x-\mu| \ge \varepsilon}p(x)dx \le \int_{|x-\mu| \ge \varepsilon} \frac{|x-\mu|^{2}}{\varepsilon^{2}}p(x)dx \\le \frac {1}{\varepsilon^{2}}\int_{-\infty}^{\infty}(x-\mu)^{2}p(x)dx=\frac{\sigma^{2}}{\varepsilon^{2}}\]
切比雪夫不等式的特殊情况:设随机变 \({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n,\cdots\) 相互独立,且具有相同的数学期望和方差 $ \mathbb E[{\mathbf x}_k] =\mu, Var[{\mathbf x}_k] =\sigma^{2},k=1,2,\cdots$ 。作 \(n\) 个随机变量的算术平均 $ \overline {\mathbf x} =\frac {1}{n} \sum _{k=1}^{n}{\mathbf x}_k$ ,则对于任意正 $ \varepsilon$ 有:
\[\lim_{n\rightarrow \infty}P\{|\overline {\mathbf x}-\mu| \lt \varepsilon\}=\lim_{n\rightarrow \infty}P\{|\frac{1}{n}\sum_{k=1}^{n}{\mathbf x}_k-\mu| \lt \varepsilon\} =1\] 证明:
\[\mathbb E[\frac{1}{n}\sum_{k=1}^{n}{\mathbf x}_k]=\mu\Var[\frac{1}{n}\sum_{k=1}^{n}{\mathbf x}_k]=\frac{\sigma^{2}}{n}\] 有切比雪夫不等式,以 \(n\) 趋于无穷时,可以证明。详细过程省略
probability mass function:PMF)为:[a,b]上均匀分布,则其概率密度函数(probability density function:PDF)为:categorical分布:它是二项分布的推广,也称作multinoulli分布。假设随机变 \(\mathbf x \in \{1,2,\cdots,K\}\) ,其概率分布函数为:曲线在 $x=\mu \pm \sigma $ 处有拐点
参 \(\mu\) 决定曲线的位置 \(\sigma\) 决定图形的胖瘦
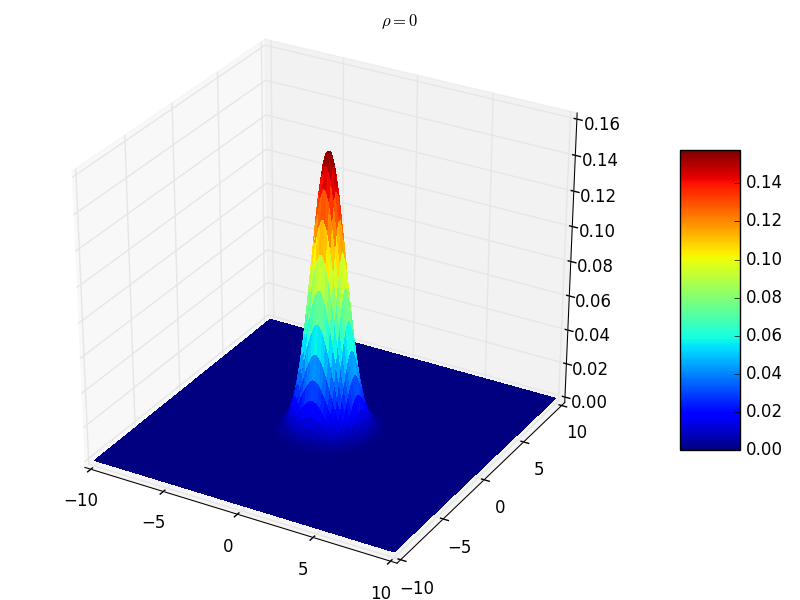
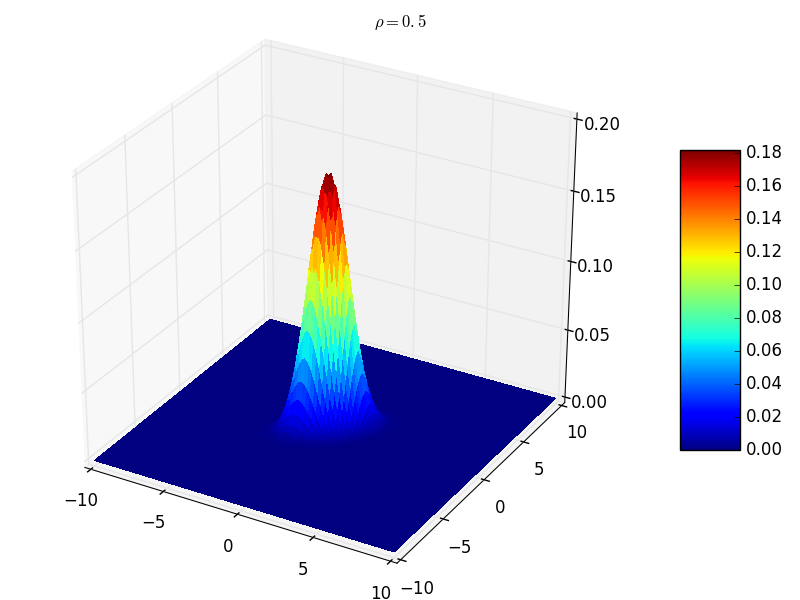
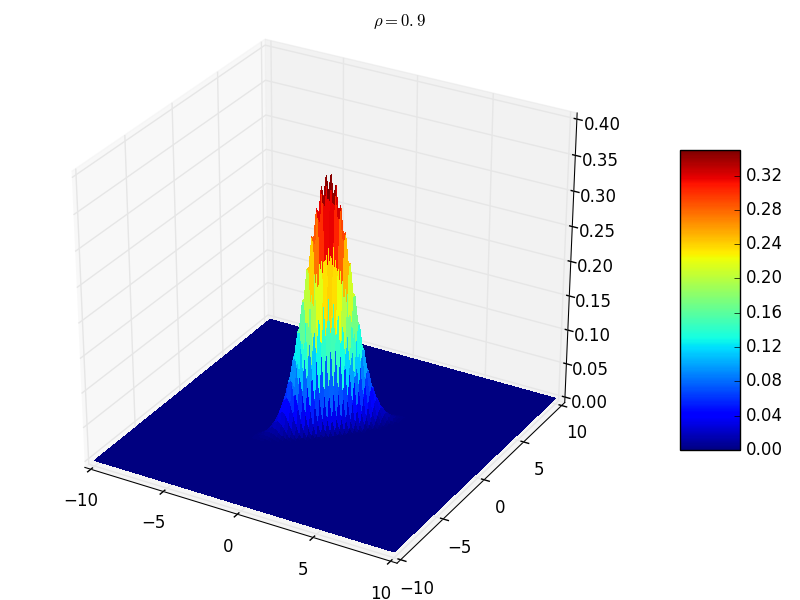
\(({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n)\) 服 \(n\) 维正态分布, \({\mathbf y}_1,{\mathbf y}_2,\cdots,{\mathbf y}_k\) \({\mathbf x}_j,j=1,2,\cdots,n\) 的线性函数, \(({\mathbf y}_1,{\mathbf y}_2,\cdots,{\mathbf y}_k)\) 也服从多维正态分布
这一性质称为正态变量的线性变换不变性
- \(({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n)\) 服 \(n\) 维正态分布, \({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n\) 相互独 \(\Longleftrightarrow\) \({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n\) 两两不相关
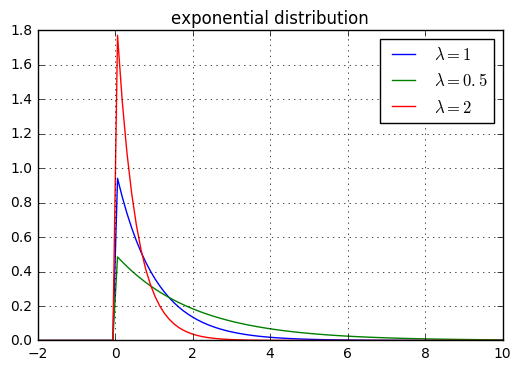
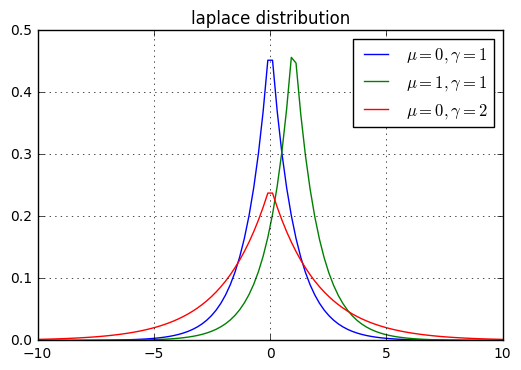
multinoulli分布,它简单地等于训练集中的经验频率。multinoulli分布来决定选用哪个分量,然后由该分量的分布函数来生成样本。multinoulli分布 \(c\) 的取值范围就是各分量的编号。先验分布+数据(似然)= 后验分布self-information为:(A,B,C,D)的样本集中,真实分 \(P=(\frac 12,\frac 12,0,0)\) ,则只需要1位编码即可识别样本。KL散度:对于给定的随机变 \(\mathbf x\) ,它的两个概率分布函 \(P(x)\) \(Q(x)\) 的区别可以用KL散度来度量:KL散度非负。当它为0时,当且仅当 P和Q是同一个分布(对于离散型随机变量),或者两个分布几乎处处相等(对于连续型随机变量)cross-entropy \(H(P,Q)=H(P)+D_{KL}(P||Q)=-\mathbb E_{\mathbf x\sim P}\log Q(x)\) 。overflow和下溢出underflow:
softmax函数。softmax函数定义为:softmax函数的每个分量的理论值都 \(\frac 1n\)
此 \(\log \text{softmax}(\mathbf{\vec x})\) 趋向于负无穷,非数值稳定的。因此需要设计专门的函数来计 \(\log\text{softmax}\) ,而不是 \(\text{softmax}\) 的结果传递 \(\log\) 函数。
通常 \(\text{softmax}\) 函数的输出作为模型的输出。由于一般使用样本的交叉熵作为目标函数,因此需要用 \(\text{softmax}\) 输出的对数。
softmax名字的来源是hardmax。hardmax把一个向 $\mathbf{\vec x} $ 映射成向 \((0,\cdots,0,1,0,\cdots,0)^T\) 。即 \(\mathbf{\vec x}\) 最大元素的位置填充1,其它位置填充0。softmax会在这些位置填充0.0~1.0之间的值(如:某个概率值)。Conditioning刻画了一个函数的如下特性:当函数的输入发生了微小的变化时,函数的输出的变化有多大。
Conditioning较大的函数,在数值计算中可能有问题。因为函数输入的舍入误差可能导致函数输出的较大变化。condition number为:directional derivative定义为:line search若梯 \(|\mathbf {\vec g}_k| \lt e\) ,则停止迭代 \(\mathbf {\vec x}^*=\mathbf {\vec x}\)
即此时导数为0
若梯 \(|\mathbf {\vec g}_k| \ge e\) ,则 \(\mathbf {\vec p}_k=-\mathbf {\vec g}_k\) , \(\epsilon_k\) \(\epsilon_k =\min_{\epsilon \le 0}f(\mathbf {\vec x}^{<k>}+\epsilon \mathbf {\vec p}_k)\)
通常这也是个最小化问题。但是可以给定一系列 \(\epsilon_k\) 的值:如
[10,1,0.1,0.01,0.001,0.0001]然后从中挑选
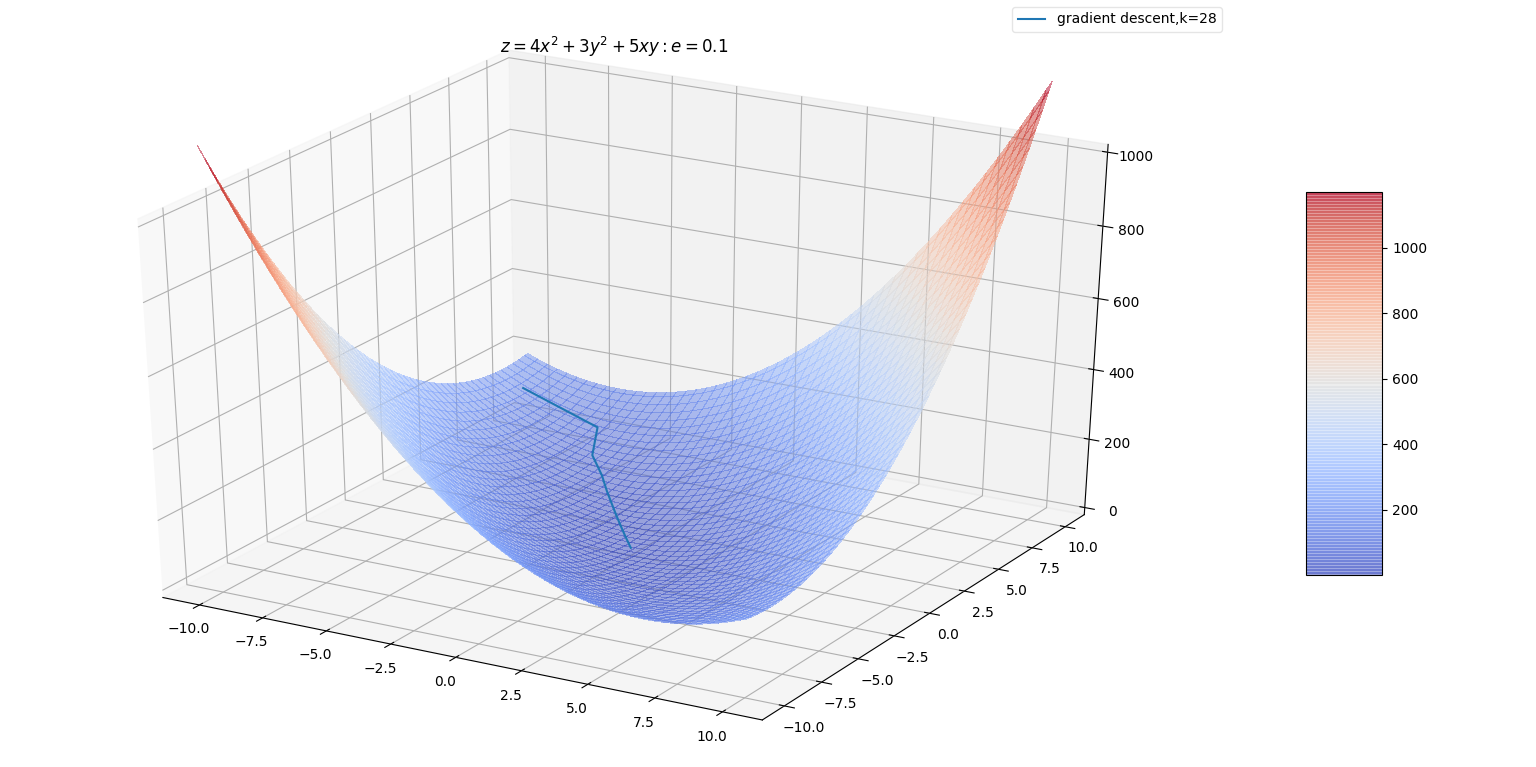
(0,1)之间。且与 \(\mathbf{\vec d}\) 夹角越小的特征向量对应的特征值具有更大的权重。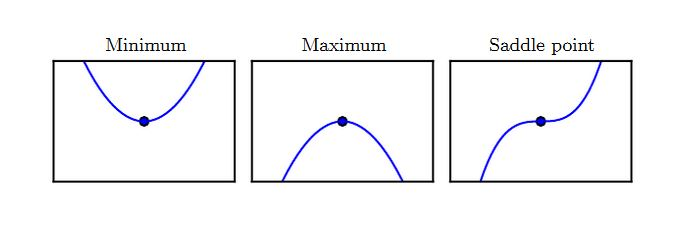
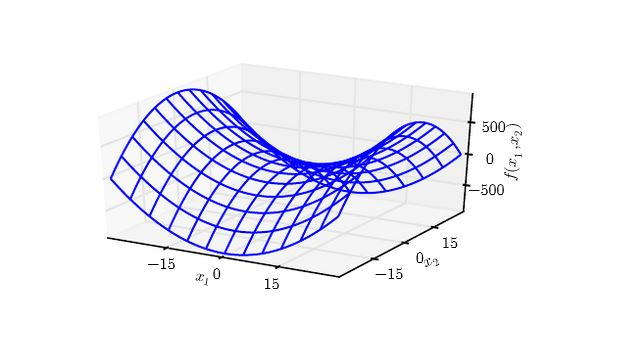
梯度下降法未能利用海森矩阵,也就不知道应该优先搜索导数长期为负的方向。
本质上应该沿着负梯度方向搜索。但是沿着该方向的一段区间内,如果导数一直为负,则可以直接跨过该区间。前提是:必须保证该区间内,该方向导数一直为负。
但是如果步长太小,对于曲率较小的地方(对应着较小的二阶导数,即该区域比较平缓)则推进太慢。
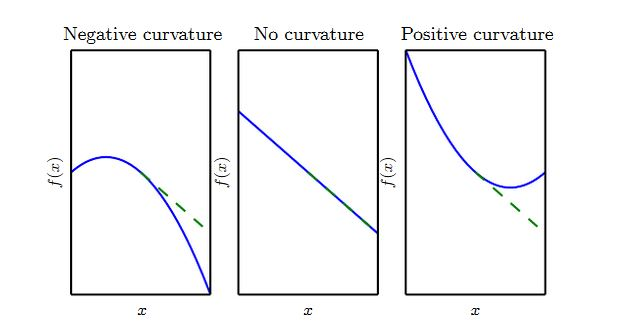
曲率刻画弯曲程度,曲率越大则曲率半径越小
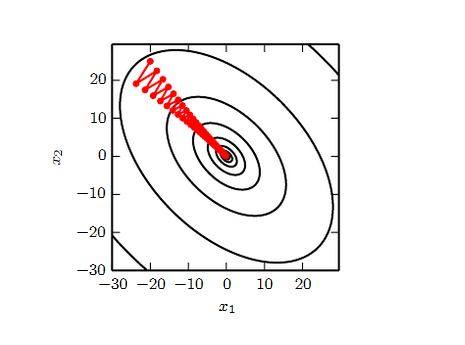
一维情况下,梯度下降法和牛顿法的原理展示:
Lipschitz连续,或者其导数Lipschitz连续。
Lipschitz连续的定义:对于函数 \(f\) ,存在一个Lipschitz常数 \(\mathcal L\) ,使得Lipschitz连续的意义是:输入的一个很小的变化,会引起输出的一个很小的变化。
与之相反的是:输入的一个很小的变化,会引起输出的一个很大的变化
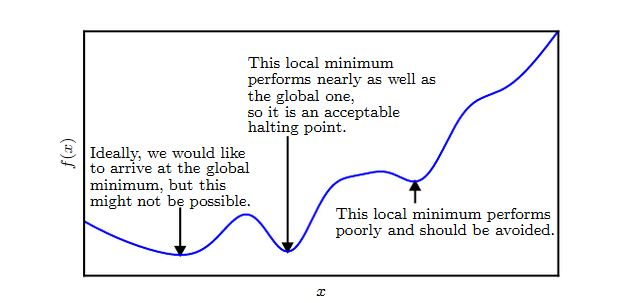
凸优化在某些特殊的领域取得了巨大的成功。但是在深度学习中,大多数优化问题都难以用凸优化来描述。
凸优化的重要性在深度学习中大大降低。凸优化仅仅作为一些深度学习算法的子程序。
\(\mathbf G_k\) 满足拟牛顿条件 \(\mathbf G_{k+1}\mathbf {\vec y}_k=\vec \delta_k\)
因 \(\mathbf G_0\) 是给定的初始化条件,所以下标 \(k+1\) 开始
按照拟牛顿条件,在每次迭代中可以选择更新矩 \(\mathbf G_{k+1}=\mathbf G_k+\Delta \mathbf G_k\)
Cholesky)分解。Davidon-Fletcher-Powell)选 \(\mathbf G_{k+1}\) 的方法是:这样 \(\mathbf P_k,\mathbf Q_k\) 不止一个。例如取
\[\mathbf P_k=\frac{\vec \delta_k\vec \delta_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k},\quad \mathbf Q_k=-\frac{\mathbf G_k\mathbf {\vec y}_k \mathbf {\vec y}_k^{T} \mathbf G_k}{\mathbf {\vec y}_k^{T}\mathbf G_k \mathbf {\vec y}_k}\] ?
这 \(\vec \delta_k,\mathbf {\vec y}_k\) 都是列向量
则迭代公式为:
\[\mathbf G_{k+1}=\mathbf G_k+\frac{\vec \delta_k\vec \delta_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k}-\frac{\mathbf G_k\mathbf {\vec y}_k \mathbf {\vec y}_k^{T} \mathbf G_k}{\mathbf {\vec y}_k^{T} \mathbf G_k \mathbf {\vec y}_k}\]
其中的向 \(\vec \delta_k,\mathbf {\vec y}_k\) 都是列向量
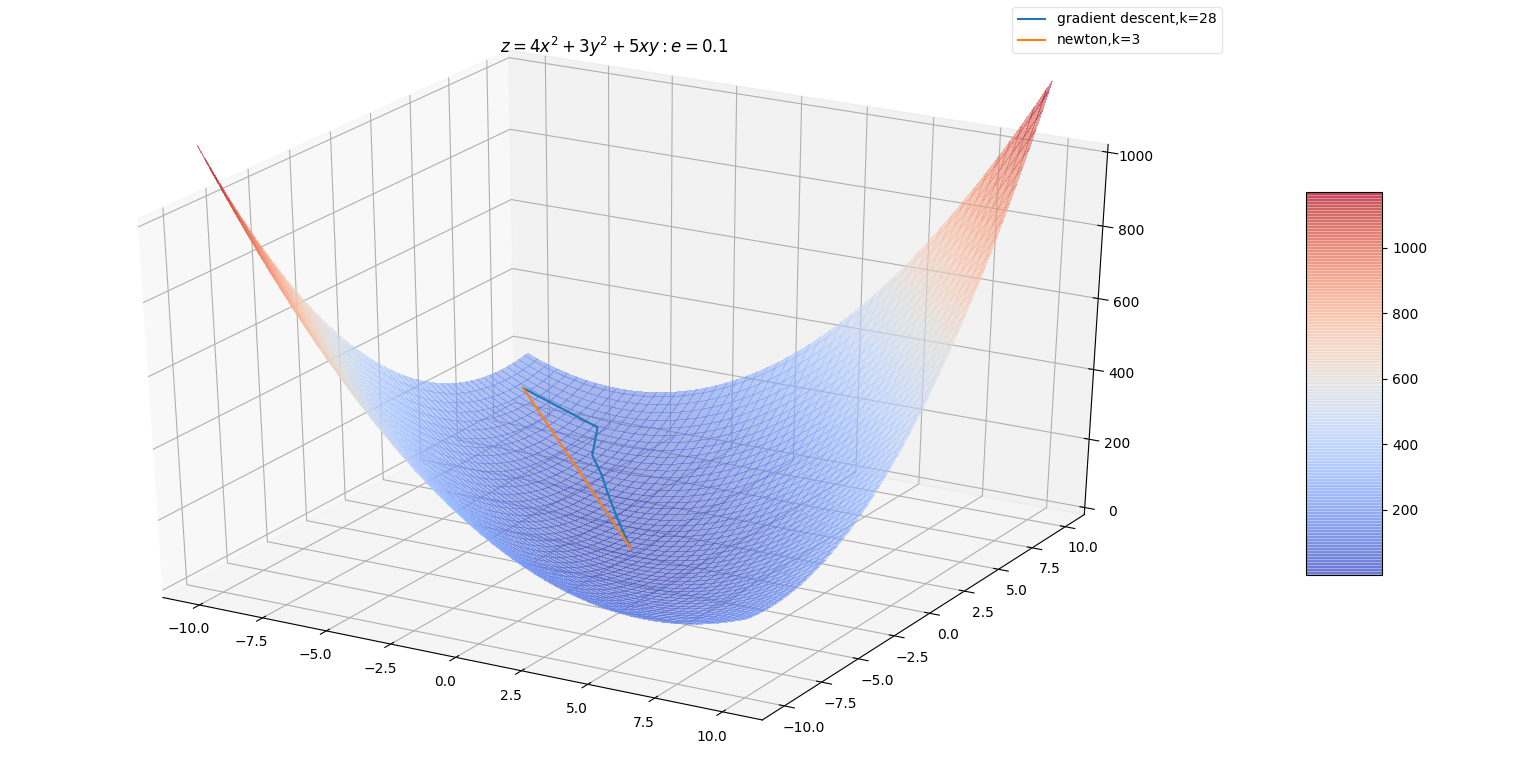
DFP算法中,每一 \(\mathbf {\vec x}\) 增加的方向 \(-\mathbf G_k \nabla_k\) 的方向。增加的幅度 \(\epsilon_k\) 决定,若跨度过大容易引发震荡
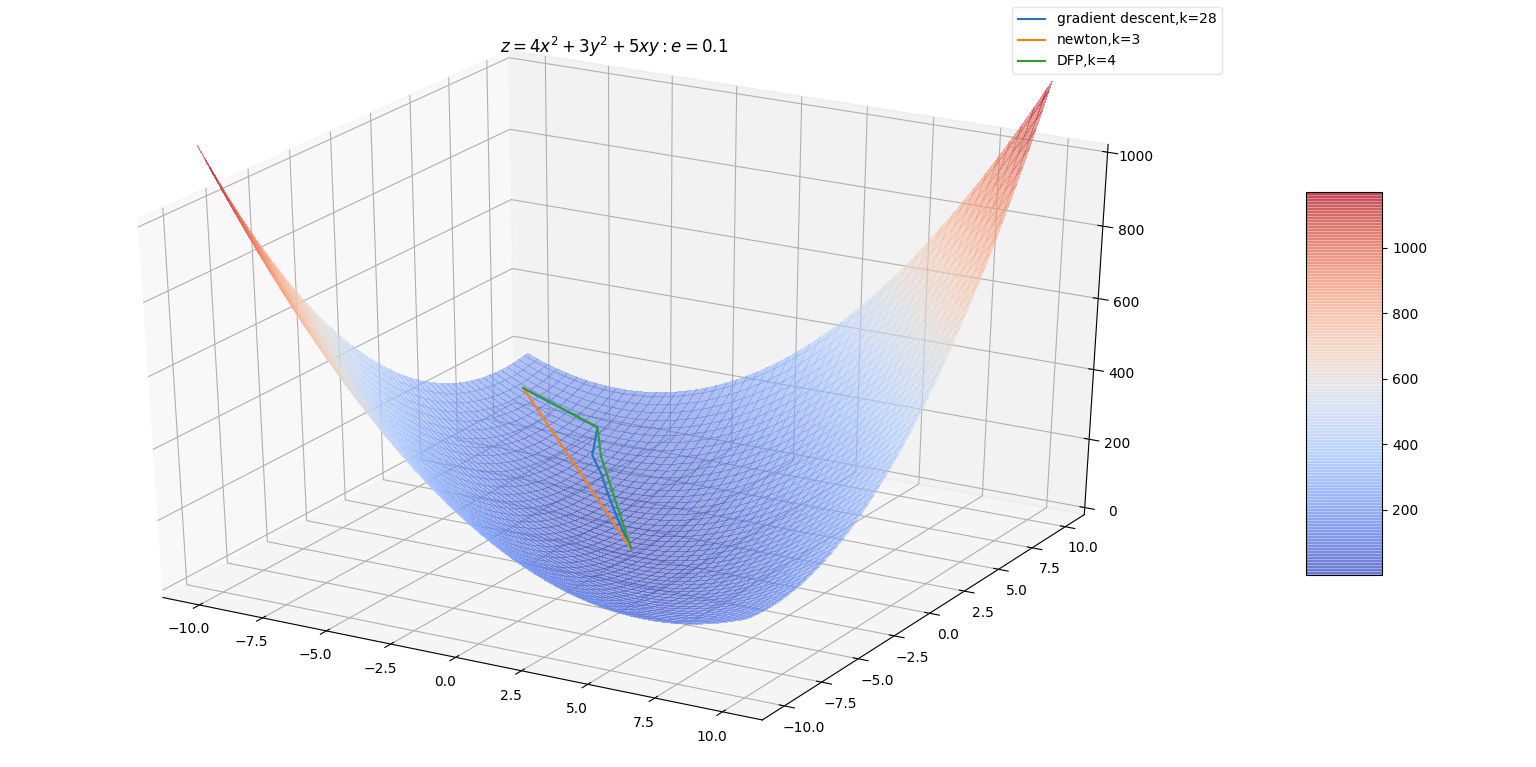
BFGS是最流行的拟牛顿算法。DFP算法中, \(\mathbf G_k\) 逼 \(\mathbf H^{-1}\) 。换个角度可以用矩 \(\mathbf B_k\) 逼近海森矩 \(\mathbf H\) 。此时对应的拟牛顿条件为 \(\mathbf B_{k+1}\vec \delta_k=\mathbf {\vec y}_k\) 。
因 \(\mathbf B_0\) 是给定的初始化条件,所以下标 \(k+1\) 开始
令 \(\mathbf B_{k+1}=\mathbf B_k+\mathbf P_k+\mathbf Q_k\) ,有 \(\mathbf B_{k+1}\vec \delta_k=\mathbf B_k\vec \delta_k+\mathbf P_k\vec \delta_k+\mathbf Q_k\vec \delta_k\)
可以 \(\mathbf P_k\vec \delta_k=\mathbf {\vec y}_k,\mathbf Q_k\vec \delta_k=-\mathbf B_k\vec \delta_k\) 。寻找合适 \(\mathbf P_k,\mathbf Q_k\) ,可以得到BFGS算法矩阵 \(\mathbf B_{k+1}\) 的迭代公式:
\[\mathbf B_{k+1}=\mathbf B_k+\frac{\mathbf {\vec y}_k\mathbf {\vec y}_k^{T}}{\mathbf {\vec y}_k^{T}\vec \delta_k}-\frac{\mathbf B_k\vec \delta_k\vec \delta_k^{T}\mathbf B_k}{\vec \delta_k^{T}\mathbf B_k\vec \delta_k}\]
其中的向 \(\vec \delta_k,\mathbf {\vec y}_k\) 都是列向量
\(\mathbf B_k\mathbf {\vec p}_k=-\mathbf {\vec g}_k\) 求 \(\mathbf {\vec p}_k\)
这里表面上看需要对矩阵求逆。但是实际 \(\mathbf B_k^{-1}\) 有迭代公式。根据
Sherman-Morrison公式以 \(\mathbf B_k\) 的迭代公式,可以得 \(\mathbf B_k^{-1}\) 的迭代公式
BFPS算法中,每一 \(\mathbf {\vec x}\) 增加的方向 \(-\mathbf B_k^{-1} \nabla_k\) 的方向。增加的幅度 \(\epsilon_k\) 决定,若跨度过大容易引发震荡
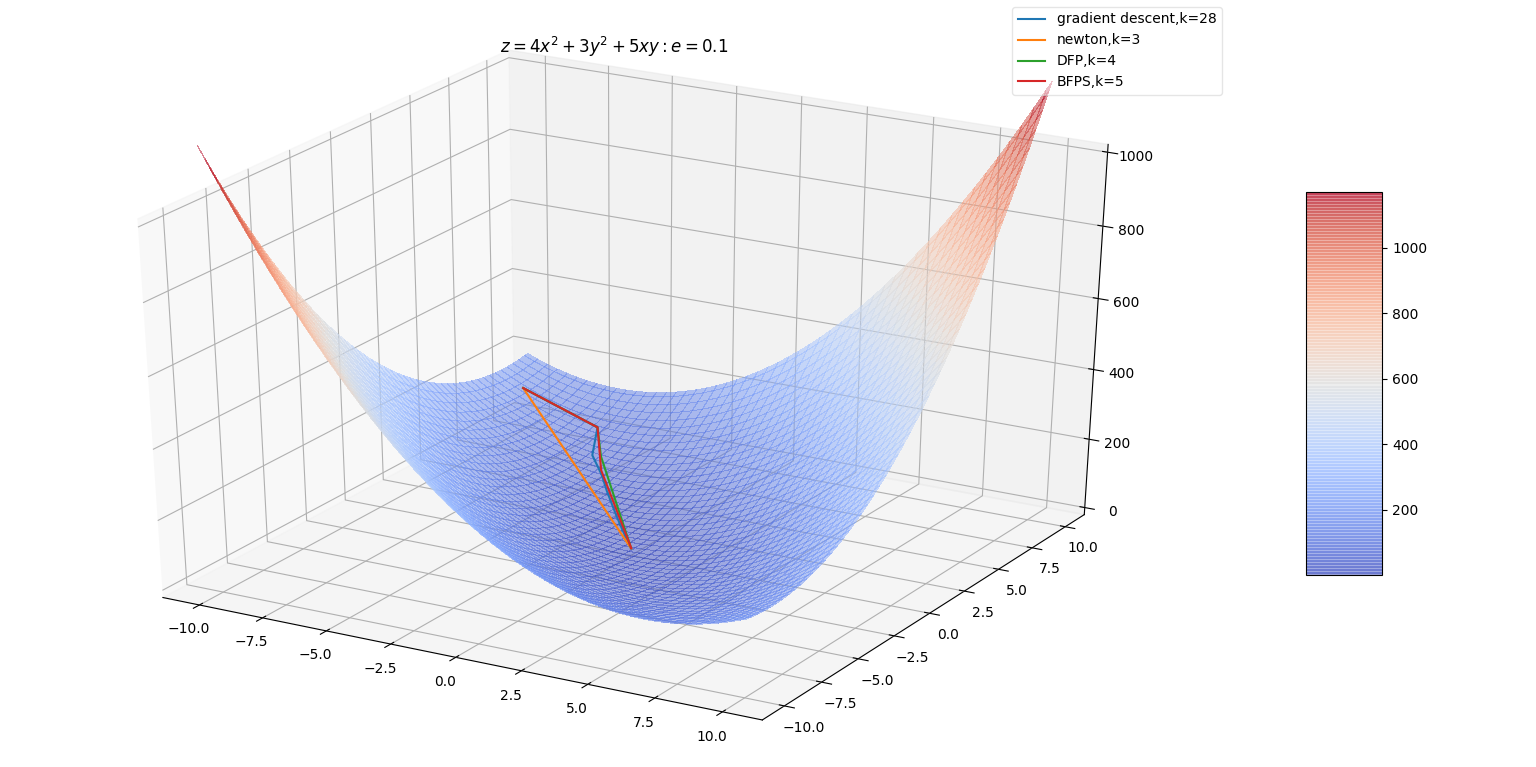
Sherman-Morrison公式可得:Sherman-Morrison公式:假 \(\mathbf A\) \(n\) 阶可逆矩阵 \(\mathbf {\vec u},\mathbf {\vec v}\) \(n\) 维列向量, \(\mathbf A+\mathbf {\vec u}\mathbf {\vec v}^{T}\) 也是可逆矩阵,则:?
?
\[d^*=\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0}\theta_D(\vec \alpha,\vec\beta)\]
Karush-kuhn-Tucker(KKT)条件:sigmoid函数:
softplus函数:softplus,因为它是下面函数的一个光滑逼近:
sigmoid和softplus函数的性质:logit函数
Erlang分布本文转载自华校专老师博客,博客地址:http://www.huaxiaozhuan.com/
标签:poi psc ilo VID 特性 特征 最优 系统 最优化问题
原文地址:https://www.cnblogs.com/guoyaohua/p/9905760.html