数据结构——第二章树和森林：04哈夫曼树与哈夫曼编码

标签：src   bubuko   算法   树根   因此   数据   次数   分享图片   其它   

1.结点的路径长度：从根结点到该结点的路径上分支的数目。

2.树的路径长度：树中每个结点的路径长度之和。

3.树的带权路径长度：树中所有叶子结点的带权路径长度之和WPL(T) = ∑w_kl_k（对所有叶子结点）

4.最优树：在所有含n个结点，并带相同权值的m叉树中，必存在一棵其带权路径长度取最小值的树，称为最优树。

5.哈夫曼算法构造最优树：以二叉树为例：

（1）根据给定的n个权值{w₁, w₂, ... , w_n}构造n棵二叉树的集合F = {T₁, T2, ... ,Tn}，其中每棵二叉树中均只含一个带权值为w_i的根结点，其左、右子树为空树；

（2）在F中选取其根结点的权值为最小的两棵二叉树，分别作为左、右子树构造一棵新的二叉树，并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和；

（3）从F中删除这两棵树，同时加入刚生成的新树；

（4）重复（2）（3），直至F中只含一棵树为止。

例如：已知权值 W= {5, 6, 2, 9, 7}

分析：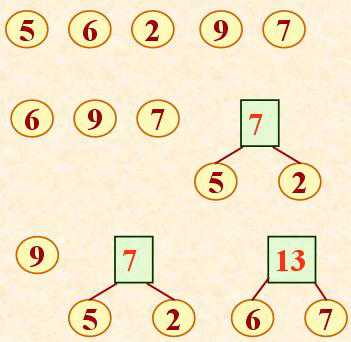

答案：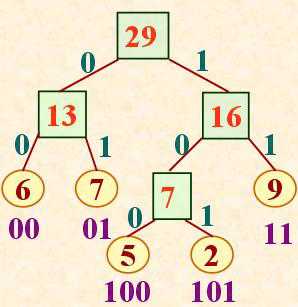

6.前缀编码：指的是，任何一个字符的编码都不是同一字符集中另一个字符的编码的前缀。利用赫夫曼树可以构造一种不等长的二进制编码，并且构造所得的赫夫曼编码是一种最优前缀编码，即使得所传电文的总长度最短。

例如：数据传送中的二进制编码，要传送数据state、seat、act、tea、cat、set、a、eat，如何使传送的长度最短？

答：首先规定二叉树的构造为左走0，右走1。为了保证长度最短，先看字符出现的次数，然后将出现次数当作权（a出现7次，c出现2次，e出现5次，s出现3次，t出现8次）。根据上述构造哈夫曼树可以得到各字母的哈夫曼编码：a——10，c——000，e——01，s——001，t——11，所以state的编码为00111101101，该构造满足哈夫曼编码的最短最优性质：

①若两字母不同，则对应的树叶不同，因此前缀码（任一字符的编码都不是另一个字符编码）不同，一个路径不可能是其它路径的一部分，所以字母之间可以完全区别。

②将所有字符变成二进制的哈夫曼编码，使带权路径长度最短。

数据结构——第二章树和森林：04哈夫曼树与哈夫曼编码

标签：src   bubuko   算法   树根   因此   数据   次数   分享图片   其它   

原文地址：https://www.cnblogs.com/hou36/p/9907650.html