标签:oid 好的 系统 特征 目标变量 span ref 接下来 原因
虽然叫做“回归”,但是这个算法是用来解决分类问题的。回归与分类的区别在于:回归所预测的目标量的取值是连续的(例如房屋的价格);而分类所预测的目标变量的取值是离散的(例如判断邮件是否为垃圾邮件)。当然,为了便于理解,我们从二值分类(binary classification)开始,在这类分类问题中,y只能取0或1。更好的理解问题,先举个小例子:假如我们要制作一个垃圾邮件过滤系统,如果一封邮件是垃圾系统,y=1,否则y=0 。给定训练样本集,当然它们的特征和label
都已知,我们就是要训练一个分类器,将它们分开。
提醒:
不要用线性回归问题去解决分类问题,这是AndrewNG给出的一个忠告!原因很简单,看下图:
看着效果还不错吧,那你在看看下图:
不靠谱吧,只是多了几个正类的点而已,分类线就发生了很大的变化。
解决方法:
为了解决这个问题,我们提出了新的假设函数:
,
其中:
图像:
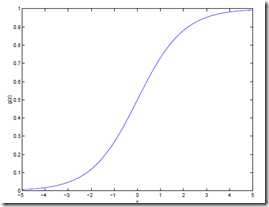
我们把这个函数叫做logistic函数,或者sigmoid函数。
我们可以发现,当z趋向无穷时,g(z)趋向于1;当z趋向于负无穷时,g(z)趋向于0 ,即当z从负无穷到正无穷的变化时,现在看来,g(z)从0变化到1 ,且g(0)=0.5 。我们要预测的值为0或1,g(z)的变化范围恰好为(0,1),我们想到概率的取值也为(0,1)哈,那索性就用g(z)表示一概率值吧,所以我们假设:
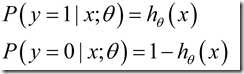
也可以写成:
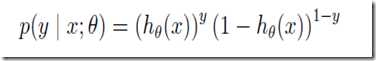
下面我们就要用到极大似然原理:一件事情已经发生了,我们就认为这件事情发生的概率最大,用关于参数的函数来表示出这个概率,求出其最大值所对应的参数值就是我们的目的。在们问题中,给出一个训练集(大小为m),其和
都已知,也就是这件事情已经发生,那我们就求其概率,令其最大:
似然函数:
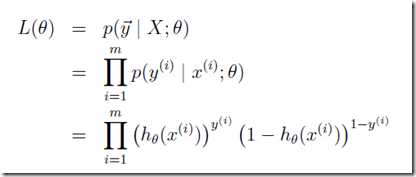
便于计算,要对其取对数:
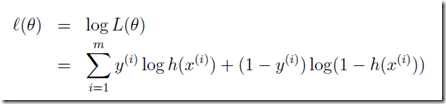
接下来的问题就是要求这个函数的极大值了,很简单,梯度下降法啦:
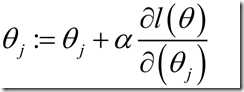
注意其实应该叫做梯度上升法,梯度下降法是“-”,但这里求极大值,所以是“+”。
其中求偏导的部分由:
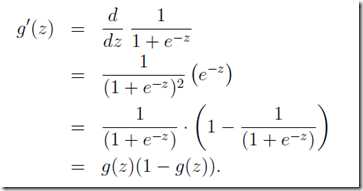
得到:
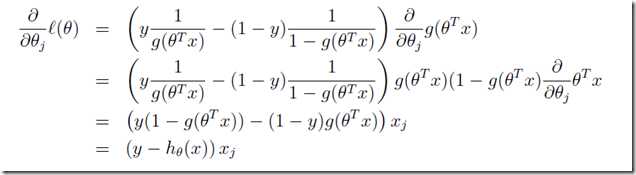
最终,我们得到参数的更新法则:
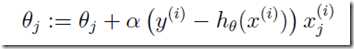
【模式识别与机器学习】——logistic regression
标签:oid 好的 系统 特征 目标变量 span ref 接下来 原因
原文地址:https://www.cnblogs.com/chihaoyuIsnotHere/p/9922493.html