标签：初始   好的   最小   ide   联合   limits   距离   优化   衡量   

1.线性回归

对包含$d$个属性描述的数据${\bf{x}} = \{ {x_1},{x_2},...,{x_d}\}$，建立一个加权线性模型，$f({\bf{x}}) = {\omega _1}{x_1} + {\omega _2}{x_2} + ... + {\omega _d}{x_d} + b$，尽可能预测地准确对应的标签值$y$，各权重$\omega$直观表达了各属性在预测中的重要性，因此线性模型有很好的可解释性。

我们先考虑最简单的情况，$d=1$。线性回归试图学得$f(x_i) = {\omega }^T {x_i}+ b$，使得$f(x_i) \simeq {y_i}$。如何衡量这两个之间的差别呢？均方误差是回归任务中最常用的性能度量，因此我们可以试图让均方误差最小化，

\[\begin{array}{*{c}}
{({\omega ^*},{b^*}) = \mathop {\arg \min }\limits_{\omega ,b} \sum\limits_{i = 1}^m {{{\left( {f({x_i}) - {y_i}} \right)}^2}} }\\
{ = \mathop {\arg \min }\limits_{\omega ,b} \sum\limits_{i = 1}^m {{{\left( {{\omega ^T}{x_i} + b - {y_i}} \right)}^2}} }
\end{array}\]

均方误差有非常好的几何意义，对应了欧氏距离。基于均方误差最小化来进行求解的方法成为“最小二乘法”。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小。

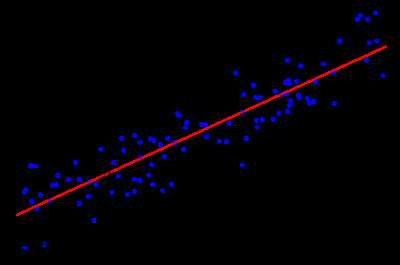
求解$\omega$和$b$使$E(\omega ,b) = \sum\limits_{i = 1}^m {{{\left( {{\omega ^T}{x_i} + b - {y_i}} \right)}^2}} $最小化的过程，称之为线性回归模型的最小二乘“参数估计”。由于$E(\omega ,b) $是凸函数，令$\omega$和$b$的偏导为零，可以求其最优解的闭式解。 

。。。待补充

更一般的情况，针对数据集$D = \{ ({{\bf{x}}_1},{y_1}),({{\bf{x}}_2},{y_2}),...,({{\bf{x}}_m},{y_m})\} $，其中${{\bf{x}}_i} = \{ {x_{i1}},{x_{i2}},...,{x_{id}}\} $，包含d维特征。试图学得$f({{\bf{x}}_i}) = {{\bf{\omega }}^T}{{\bf{x}}_i} + b$，使得$f({\bf{x}_i}) \simeq {y_i}$，这称之为“多元线性回归”。类似用最小二乘法求得$\bf{\omega}$和$b$最优解的闭式解，但涉及矩阵逆计算，要复杂很多。

。。。待补充

线性回归模型的一般形式为：

\[y = {{\bf{\omega }}^T}{\bf{x}} + b\]

如果我们的数据是成指数变化的，那么可以把线性回归模型扩展为：

\[\ln y = {{\bf{\omega }}^T}{\bf{x}} + b\]

更一般的，考虑单调可微函数$g(\bullet)$，将线性回归模型的预测值与真实标记联系起来，那么线性回归模型扩展为：

\[y = {g^{ - 1}}({{\bf{\omega }}^T}{\bf{x}} + b)\]

2. logistic回归

那怎么把线性回归模型扩展到分类模型中呢，找一个单调可微函数，将线性回归模型的预测值与真实类别联系起来。

考虑二分类问题，单位阶跃函数是理想的分类函数，若预测值大于0则为{1}正类，小于0则为{0}负类，等于0则可任意判别。但是这样的阶跃函数不连续，不是可微的。因此我们利用对数几率函数（logistic function）来近似单位阶跃函数。

\[y = \frac{1}{{1 + {e^{ - z}}}}\]

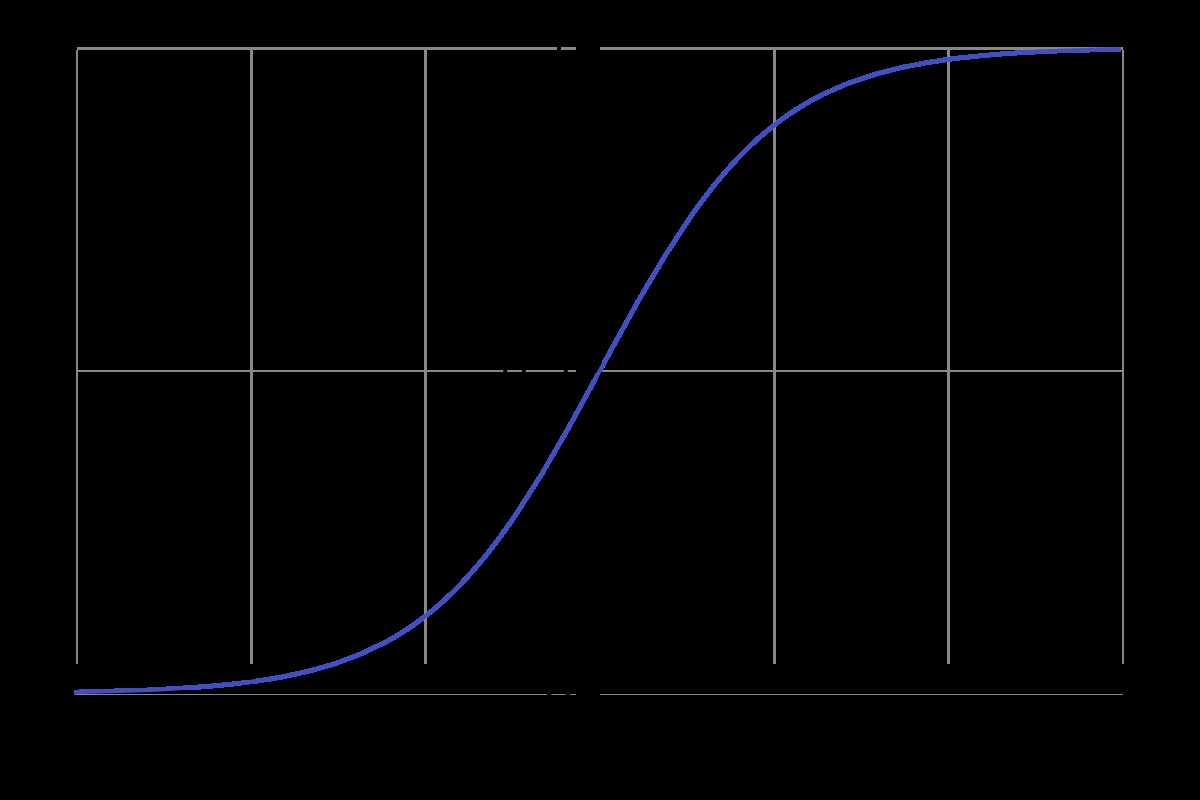
将z值转化成一个接近于0或1的y值。

\[\ln \frac{y}{{1 - y}} = {{\bf{\omega }}^T}{\bf{x}} + b\]

 \[\ln \frac{{p(y = 1|x)}}{{p(y = 0|x)}} = {{\bf{\omega }}^T}{\bf{x}} + b\]

该模型是在用线性回归模型的预测值去逼近真实标记的对数（$\ln$）几率（$\frac{y}{1 + y}$），其对应的模型成为“logistic回归”。

视y为类后验概率估计$p(y=1|x)$，有：

\[y = p(y = 1|x) = \frac{1}{{1 + {e^{ - {{\bf{\omega }}^T}{\bf{x}} - b}}}}\]

\[y = p(y = 1|x) = \frac{1}{{1 + {e^{  {{\bf{\omega }}^T}{\bf{x}} + b}}}}\]

极大似然估计的思想为：对于所有的抽样样本，使它们联合概率达到最大的系数便是统计模型最优的系数。

给定数据集D，logistic回归模型最大化“对数似然”

\[l({\bf{w}},b) = \sum\limits_{i = 1}^m {\ln p({y_i}|{{\bf{x}}_i};{\bf{w}},b)} \]

为了便于讨论，令$\bf{\beta}= ({\bf{w}};b)$，$\widehat{\bf{x}}= (\bf{x};1)$，对数似然等价为最小化

\[l({\bf{\beta }}) = \sum\limits_{i = 1}^m {( - {y_i}{{\bf{\beta }}^T}{{\widehat {\bf{x}}}_i} + \ln (1 + {e^{{{\bf{\beta }}^T}{{\widehat {\bf{x}}}_i}}}))} \]

可根据经典数值优化算法如梯度下降法等求得其$\bf{\beta }$的最优解，

\[{{\bf{\beta }}^*} = \mathop {\arg \min }\limits_{\bf{\beta }} l({\bf{\beta }})\]

logistic回归算法

输入：训练集$D = \{ ({{\bf{x}}_1},{y_1}),({{\bf{x}}_2},{y_2}),...,({{\bf{x}}_m},{y_m})\} $；

           学习率$\alpha$;

　　　终止条件$\varepsilon$.

过程：

1：令$\bf{\beta}= ({\bf{w}};b)$，$\widehat{\bf{x}}= (\bf{x};1)$

2：针对$l({\bf{\beta }}) = \sum\limits_{i = 1}^m {( - {y_i}{{\bf{\beta }}^T}{{\widehat {\bf{x}}}_i} + \ln (1 + {e^{{{\bf{\beta }}^T}{{\widehat {\bf{x}}}_i}}}))} $

      利用随机梯度下降法求最优解${{\bf{\beta }}^*} = \mathop {\arg \min }\limits_{\bf{\beta }} l({\bf{\beta }})$

3：初始化$\bf{\beta}_0$

4：repeat

5：从训练集D中随机挑选一个数据${\bf{x}_i}, y_i$

6：以学习率$\alpha$的速度朝梯度下降的方向更新参数$\bf{\beta}$

7：end for

8：until $\Delta {\bf{\beta }} \le \varepsilon $

输出：logistic回归模型参数$\bf{w},b$

参考：

机器学习西瓜书 周志华

一、线性模型

标签：初始   好的   最小   ide   联合   limits   距离   优化   衡量   

原文地址：https://www.cnblogs.com/yijuncheng/p/9928045.html