标签:好的 ide 下一步 子节点 src some for 游戏 spl
刘杨的机器学习终于上完了惹,下周就要考试了,赶紧复习ing......
趁机做个总结,就当是复习了惹......
简单来说,就是一个三元组<P, T, E>
P——performance性能(对应着性能的评估函数,也就是常说的loss或者likelihood)
T——task任务(对应着被优化的对象,也就是目标函数)
E——experience经验
就是我们想要某种算法,这种算法的目的是提高某项任务的性能,怎么提升呢?通过已有的经验。
一个经常被引用的定义是:
A computer program is said to learn from experience E, with respect to some class of tasks T, and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
语音识别器、翻译机;对象识别;机器人控制(自动驾驶);文本挖掘;生物信息学;etc,.
①监督学习
Given D = {Xi, Yi} learn F(?; θ) s.t.: Yi = F(Xi) Dnew = {Xj} → {Yj}
Xi是我们的数据集,有m维特征,一共N个数据,X是一个m×N的矩阵;
Yi是数据集的标签,和Xi一一对应,可以有{y1, y2, ..., yk}k种取值,Y是一N×1的列向量;
监督学习的意思是数据集打好了标签,这个标签和数据有一定的关联,但是我们不知道,所以我们想办法找到另一个函数去拟合这个未知的函数。最后给一些新的数据Dnew来检验这个拟合的函数,只给定X的特征,去检验得出的结果Y。
②无监督学习
Given D = {Xi} learn F(?; θ) s.t.: Yi = F(Xi) Dnew = {Xj} → {Yj}
无监督学习的意思是只给数据集,没有标签,我们去给这个数据集打上标签,也就是分类,寻找某一种算法F,来做X到Y的某一种映射。
③强化学习(刘杨说会讲一点最后还是没讲惹)
Given D = {env, actions, rewards, simulator/trace/real game}
learn policy: e, r → a / utility: a, e → r s.t.: {env, new real game} → a1, a2, a3, ...
强化学习的意思是给定某一个环境下的某些行为,例如说Alpha Go学习下棋,机器学习的是某一种规则,在什么样的环境下,有什么样的激励会采取某种行动;或者学习某种功能,在什么样的环境下,采取什么样的行为会有什么样的激励。那么最终的目的是使得在一局新的游戏中,我们能够使得机器一步一步地采取行动。
设置:
示例集合X
未知的目标函数?:X → Y
函数假设集合H = {h|h: X→Y}
目标函数?的训练样本{<xi, yi>}
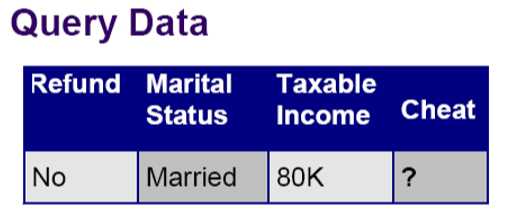
假设这是某一个人的特征,他没有还款,已婚,收入80K,那么他是否存在税务欺诈行为呢?我们该采用什么样的函数?来判断呢?
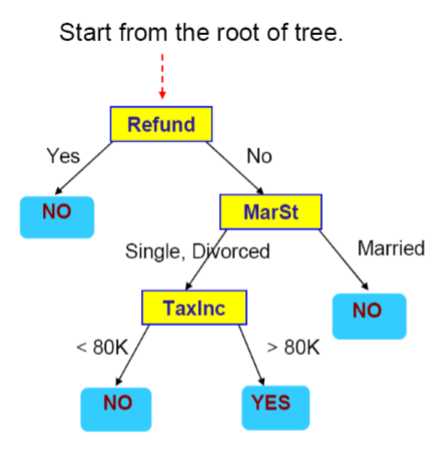
这是一棵决策树,我们用它来查询一条数据:
通过这个例子,我们看到什么是一棵决策树呢?
X = [Refund, MarSt, TaxInc]
Y = Cheat(Y取值为{Yes, No},代表是否欺诈)
就是不同的决策树
测试一个属性Xi
选择属性Xi的一个取值
预测Y

例如上图就是一种决策树的选择,当然也可以有很多种其他的决策树的选择。
决策树可以表示输入属性的任何函数。
问题:可能没有泛化的能力→希望找到一个更紧凑、更小规模的决策树
Top-Down的决策树归纳/构造算法
Main loop:
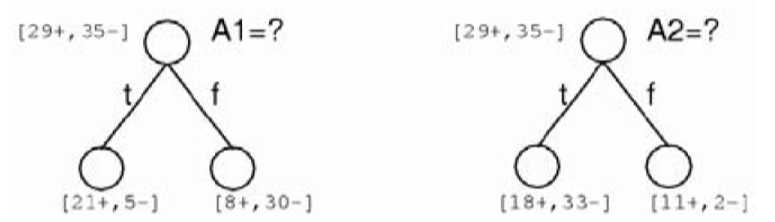
那么现在的问题就在于:
如何确定属性的测试条件?
如何确定最好的切分?
Ideology:一个好的属性切分是将示例集合切分为若干子集,最理想的情况是没给子集“皆为正例”或“皆为反例”。
所以我们更倾向节点上的数据具有同质(homogeneous)类别分布,因此一个度量来对节点的混杂度(impurity)进行测量。
随机变量X的熵为H(X):
$H(X) = -\sum_{i=1}^{N}P(x=i)\log_{2}P(x=i)$
为什么是这样的呢?
emmm香农告诉我们的...
信息论:
在最短编码情况下,对消息X = i分配$-\log_{2}P(x=i)$位,所其编码一个随机变量X的期望位数是:
$E(X) = \sum_{i=1}^{N}X \cdot P(X) = \sum_{i=1}^{N}(-\log_{2}P(x=i)) \cdot P(x=i)$
令$E(X) = H(X)$,就是我们上面的熵的公式了!
进一步地,我们有:
$X$在给定$Y = v$特定条件熵$H(X|Y=v)$:
$H(X|Y=v) = -\sum_{i=1}^{N}P(X=i|Y=v)\log_{2}P(x=i|y=v)$
$X$在给定$Y$条件熵$H(X|Y)$:
$H(X|Y) = -\sum_{j∈Val(y)}P(y=j)H(X|y=j)$
相当于遍历Y的取值,然后sum掉。
$X$和$Y$的互信息:
$I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) = H(X) + H(Y) - H(X, Y)$
假设S是训练例子的样本集,P+是样本中正例的比例,P-是样本中反例的比例,用熵来测量样本中S的混杂度:
$H(S) = -P_{+}\log_{2}P_{+} - P_{-}\log_{2}P_{-}$
标签:好的 ide 下一步 子节点 src some for 游戏 spl
原文地址:https://www.cnblogs.com/liam36/p/9932733.html