标签：计算 随机过程 情况 序列 col 贝叶斯 感受 矩阵 随机
隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔科夫过程。其难点是从可观察的参数中确定该过程的隐含参数，然后利用这些参数来作进一步的分析。在早些年HMM模型被非常广泛的应用，而现在随着机器学习的发展HMM模型的应用场景越来越小，然而在图像识别等领域HMM依然起着重要的作用。
隐马尔科夫模型是马尔科夫链的一种，它的状态不能直接观察到，但能通过观测向量序列观察到，每个观测向量都是通过某些概率密度分布表现为各种状态，每一个观测向量是由一个具有相应概率密度分布的状态序列产生。所以，隐马尔科夫模型是一个双重随机过程----具有一定状态数的隐马尔科夫链和显示随机函数集。自20世纪80年代以来，HMM被应用于语音识别，取得重大成功。到了90年代，HMM还被引入计算机文字识别和移动通信核心技术“多用户的检测”。HMM在生物信息科学、故障诊断等领域也开始得到应用。
本文以中文分子算法为实践背景基础来讲述隐马尔科夫模型。本文主要分享了隐马尔科夫模型的概率计算、参数估计和模拟预测等方法，我们能够感受大HMM能够经久不衰的强大力量。
马尔科夫模型在推导过程中用到了之前提到的一些经典算法需要融汇贯通。
概率论和数理统计、矩阵论、贝叶斯网络、EM算法
1、定义
隐马尔科夫模型(HMM,Hidden Markov Model)可用标注问题，在语音识别、NLP、生物信息、模式识别等领域被实践证明是有效的算法。
HMM是关于时序的概率模型，描述由一个隐藏的马尔科夫链生成不可观测的状态随机序列，再由各个状态生成观测随机序列的过程。
隐马尔科夫模型随机生成的状态随机序列，称为状态序列；每个状态生成一个观测，由此产生的观测随机序列，称为观测序列。
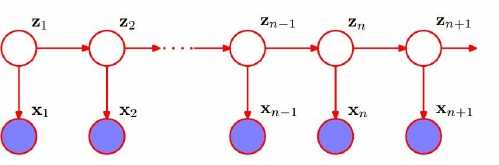
Z是未知的，X是已知的，我们通过对X来做Z的推论，就是隐马尔科夫模型。
2、HMM的确定：
HMM由初始概率分布π、状态转移概率分布A以及观测概率分布B确定。
， 
描述整个隐码模型。
3、HMM的参数：
Q是所有可能的状态的集合，N是可能的状态数；
V是所有可能的观测的集合，M是可能的观测数。
1、直接计算：
按照概率公式，列举所有可能的长度为T的状态序列
，求各个状态序列I与观测序列
的联合概率
，然后对所有可能的状态序列求和，
从而得到
。
2、前向算法
前向概率定义：给定λ，定义到时刻t部分观测序列为且状态为
且qi的概率称为前向概率，记做：
前向算法计算方案：
初值：
递推：对于t=1,2，...,T-1
有：
最终：
3、后向算法
定义：给定λ，定义到时刻t状态为qi的前提下，从t+1到T的部分观测序列为
的概率为后向概率，记做：
计算方法：
初值：
递推：对于t=T-1，T-2，...,1
最终：
1、预测的近似算法
A. 在每个时刻t选择在该时刻最有可能出现的状态it*，从而得到一个状态序列I*={i1*,i2*…iT*}，将它作为预测的结果。
B. 给定模型和观测序列，时刻t处于状态qi的概率为：
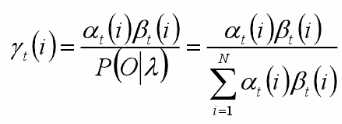
C. 选择概率最大的i作为最有可能的状态（注：会出现此状态在实际中可能不会发生的情况）
2、Viterbi算法
Viterbi算法实际是用动态规划解HMM预测问题，用DP求概率最大的路径(最优路径)，这是一条路径对应一个状态序列。
定义变量
：在时刻t状态为i的所有路径中，概率的最大值。
具体过程：
定义：
递推：
标签：计算 随机过程 情况 序列 col 贝叶斯 感受 矩阵 随机
原文地址：https://www.cnblogs.com/hxf175336/p/9934691.html
