P2520 [HAOI2011]向量

标签：就是   ret   www   log   ima   变量   clu   image   文章   

挺喜欢这个大佬的解题：https://www.cnblogs.com/five20/p/8427795.html    这篇文章也是借鉴大佬的博客。不过还是希望有别的补充。

题意：给你坐标（x, y）然后产生（x,y）（-x,y）（x,-y）（-x,-y）(y,x) (-y,x) (y,-x) (-y,-x)让这八个坐标任意组合，问是否能配成（a， b）坐标。

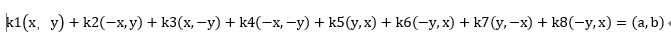然后，其实（x, y）和（-x，-y）提公因式化为同一项

其他同理 

我们先证明一个东西为后面的证明打下基础！

还可以说明 h1,h3具有同奇同偶性，　　h2,h4具有同奇同偶性

那我们来分析一下有解的情况：

　　情况一：h1+h2 为偶数， h2+h4为偶数

　　　　　　那么对于a来说一定能被gcd(x, y)*2整除。

　　情况二：h1+h2 为奇数， h2+h4为奇数

　　　　　　两边同时加x+y, 因为奇数+1等于偶数，则就是情况一：（a+x+y）%gcd(x, y)*2==0　　（为什么可以随便添加x，y，在变量中增加和减少不影响（注意：区分集合））

　　情况三：h1+h2 为奇数， h2+h4为偶数

　　　　　　两边加x,则为情况一：（a+x）%gcd(x, y)*2==0

　　情况四：h1+h2 为偶数， h2+h4为奇数

　　　　　　两边加y，则为情况一：（a+y）%gcd(x, y)*2==0

这只是说明了一个式子有解，下一个式子是相同套路。

#include<cstdio>
#define ll long long
ll k;
ll gcd(ll a, ll b){ return b == 0 ? a : gcd(b, a%b); }
bool check(ll a, ll b){ return a%k == 0 && b%k == 0; }

int main(){
    int t;
    scanf("%d", &t);
    while (t--){
        ll x, y, a, b;
        scanf("%lld%lld%lld%lld", &a, &b, &x, &y);
        k = gcd(a, b)*2;
        if (check(x, y) || check(x + a, y + b) || check(x + b, y + a) || check(x + a + b, y + a + b)){ printf("Y\n"); }
        else printf("N\n");
    }
}

P2520 [HAOI2011]向量

标签：就是   ret   www   log   ima   变量   clu   image   文章   

原文地址：https://www.cnblogs.com/ALINGMAOMAO/p/9937633.html