标签:方便 像素 技术分享 转换 影响 http 读取 nbsp 经纬
全景图是2:1比例的图片,一般是多张图像拼接而成。全景图2:1的比例可以很方便的映射到球面,而球坐标可以很方便的实现各种有趣的投影。比如小行星,水晶球,局部透视投影等。
今天来说说怎么将全景图投影到小行星视图:
首先,要有一副2:1的全景图,如下:

风景秀丽是不是。
然后,将全景图按照经纬展开法重新贴到球面,图像的宽就是纬度0-2π,图像的高就是经度0-π。
接下来,需要一种下面这样的投影。将一个球面上的坐标投影到平面上。投影中心在球心到球面之间。
从百度百科上盗的图,各位将就着看。
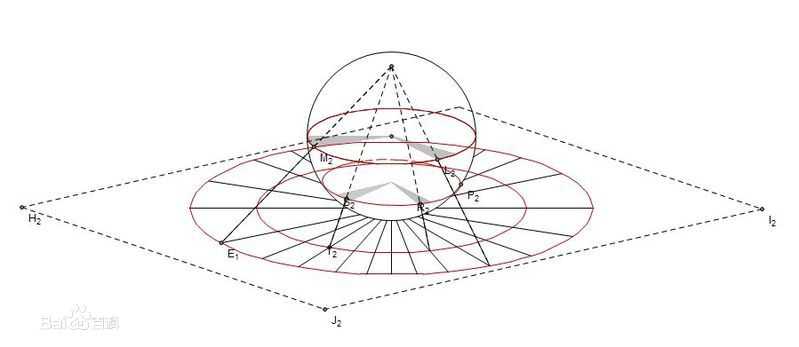
这种投影方式中,下半球面会全部投影在平面图中的一个圆内,上半球面会全部投影到圆的外面,并且分布越来越稀疏。
投影过程可以理解为:
1. 首先建立球坐标系,将经纬度的全景图贴到球面上,这个过程我之前的一篇博客中鱼眼图转经纬图讲过,原理一样。只不过是逆过程。
2. 设定投影中心点的坐标,然后连接投影中心点和球面上一点,得到一条直线。当然此时需要设置一个视场角FOV,即选择投影的视场角是多大。视场角越大,最后得到的小行星视图中间图像被挤压的越厉害。
3. 建立投影平面,以上图为例,该投影平面与球面相切与南极点。计算该直线与该投影平面的交点,即可得到投影后的平面坐标。
4. 上述三步均在球坐标系下完成,得到各个球面点的平面坐标后,根据具体想要得到的平面图像尺寸,将平面坐标转换为图像坐标。至此完成。
上述是正向投影过程,如果采用反向投影,原理类似,不过倒过来从原全景图像素点取值即可。
上述过程可以很方便用C++代码实现,读取图像的操作可以用OpenCV:
投影后得到的小行星视图如下,FOV和投影中心位置都会影响小行星在图像中的大小:
这个是投影点在北极点,FOV设置的120度

投影点在北极点,FOV=170度,则如下:

投影点在北极点与球心的中点,FOV=120度,则如下:

同样道理,如果投影点在南极点,投影平面放在北极,则如下图:

同理,如果在球体内随意移动投影点,投影得到的效果也会不同,可以实现不同视角的小行星。
标签:方便 像素 技术分享 转换 影响 http 读取 nbsp 经纬
原文地址:https://www.cnblogs.com/riddick/p/9937729.html