标签：函数 ast gibbs采样 样本 大量 parameter 加速 parse 条件
摘要：
当我们已知模型的存在，想知道参数的时候我们就可以通过采样的方式来获得一定数量的样本，从而学习到这个系统的参数。变分则是在采样的基础上的一次提升，采用相邻结点的期望。这使得变分往往比采样算法更高效：用一次期望计算代替了大量的采样。直观上，均值的信息是高密(dense)的，而采样值的信息是稀疏(sparse)的。
预备知识：
隐马尔科夫模型、EM算法
一、采样
1、为何要采样？
前提：模型已经存在，但参数未知；
n方法：通过采样的方式，获得一定数量的样本，从而学习该系统的参数。
现需要对概率密度函数f(x)的参数进行估计，若已知的某概率密度函数g(x)容易采样获得其样本，可以如何估计f(x)的参数？（若离散分布，则f(x)为概率分布律。）
一个简单粗暴的采样算法：再拒绝采样法（Rejection sampling）
利用已有的概率密度函数g(x)随机采样生成样本，拒绝不在f(x)内的样本
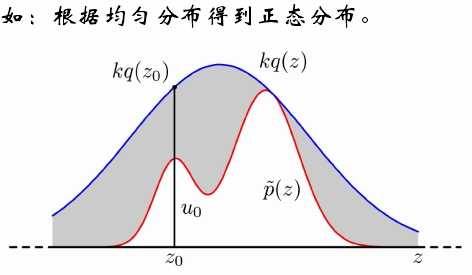
2、重述采样——马尔科夫链
采样：给定概率分布p(x)，如何在计算机中生成它的若干样本？
方法：马尔科夫链模型
考虑某随机过程π，它的状态有n个，用1~n表示。记在当前时刻t时位于i状态，它在t+1时刻位于j状态的概率为P(i,j)=P(j|i)：即状态转移的概率只依赖于前一个状态。
马尔科夫随机过程的平稳分布：初始概率不同，但经过若干次迭代，π最终稳定收敛在某个分布上。
上述平稳分布的马尔科夫随机过程对采样带来很大的启发：对于某概率分布π，生成一个能够收敛到概率分布π的马尔科夫状态转移矩阵P，则经过有限次迭代，一定可以得到概率分布π。
该方法可使用MonteCarlo模拟来完成，称之为MCMC(Markov Chain Monte Carlo)。
3、细致平稳条件
从稳定分布满足πP=π可以抽象出如下定义：如果非周期马尔科夫过程的转移矩阵P和分布π(x)满足
则π(x)是马尔科夫过程的平稳分布。
上式又被称作细致平稳条件(detailed balance condition)。
细致平稳的理解：根据定义，对于任意两个状态i，j，从i转移到j的概率和从j转移到i的概率相等。可直观的理解成每一个状态都是平稳的。
4、Matropolis-Hastings算法
假定t时刻
，采取如下策略采样
在给定
的条件分布
中采样一个值
计算M-H率
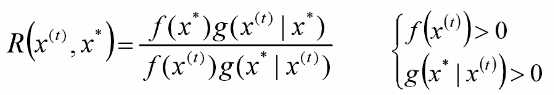
则t+1时刻
的值为
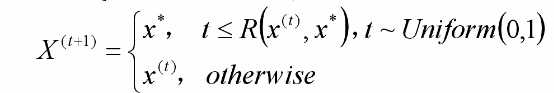
最终得到的序列收敛于f(x)分布。
5、MCMC Matropolis-Hastings算法
根据需要满足的细致平稳条件
若令
，则有：
从而：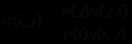
将接受率置为恒小于1，从而
初始化马尔科夫过程初始状态
对于
第t时刻马尔科夫过程初始状态
，采样
从均匀分布中采样：
则接受状态j，即
，否则，不接受状态j，
6、二维Gibbs采样算法
由：
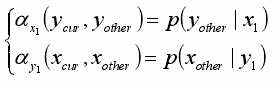
很容易得到二维Gibbs采样算法：
随机初始化：
对循环采样：
二、变分
1、Gibbs采样和变分
Gibbs采样：使用邻居结点（相同文档的词）的主题采样值
变分：采用相邻结点的期望。n
这使得变分往往比采样算法更高效：用一次期望计算代替了大量的采样。直观上，均值的信息是高密(dense)的，而采样值的信息是稀疏(sparse)的。
2、变分概述
变分既能够推断隐变量，也能推断未知参数，是非常有力的参数学习工具。其难点在于公式演算略复杂，和采样相对：一个容易计算但速度慢，一个
不容易计算但运行效率高。
平均场方法的变分推导，对离散和连续的隐变量都适用。在平均场方法的框架下，变分推导一次更新一个分布，其本质为坐标上升。可以使用模式
搜索(pattern search)、基于参数的扩展 (parameter expansion)等方案加速。
有时假定所有变量都独立不符合实际，可使用结构化平均场(structured mean field)，将变量分成若干组，每组之间独立。
变分除了能够和贝叶斯理论相配合得到VB（变分贝叶斯），还能进一步与EM算法结合，得到VBEM，用于带隐变量和未知参数的推断。
标签：函数 ast gibbs采样 样本 大量 parameter 加速 parse 条件
原文地址：https://www.cnblogs.com/hxf175336/p/9940208.html
