标签:分享 min() 教材 map接口 创建 tle 构造方法 htm sky
课程:《程序设计与数据结构》
班级: 1723
姓名: 方艺雯
学号:20172314
实验教师:王志强
实验日期:2018年11月8日
必修/选修: 必修
实验二-1-实现二叉树
参考教材p212,完成链树LinkedBinaryTree的实现(getRight,contains,toString,preorder,postorder)用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试
实验二 树-2-中序先序序列构造二叉树
基于LinkedBinaryTree,实现基于(中序,先序)序列构造唯一一棵二?树的功能,比如给出中序HDIBEMJNAFCKGL和后序ABDHIEJMNCFGKL,构造出附图中的树,用JUnit或自己编写驱动类对自己实现的功能进行测试
实验二 树-3-决策树
自己设计并实现一颗决策树
实验二 树-4-表达式树
输入中缀表达式,使用树将中缀表达式转换为后缀表达式,并输出后缀表达式和计算结果
实验二 树-5-二叉查找树
完成PP11.3
实验二 树-6-红黑树分析
参考http://www.cnblogs.com/rocedu/p/7483915.html对Java中的红黑树(TreeMap,HashMap)进行源码分析,并在实验报告中体现分析结果。(C:\Program Files\Java\jdk-11.0.1\lib\src\java.base\java\util)
getRight方法核心代码为
LinkedBinaryTree<T> result = new LinkedBinaryTree <T>();
result.root = root.getRight();preorder,postorder方法核心代码为
//前序遍历
public void preOrder(BinaryTreeNode<T> root) {
if (root != null) {
System.out.print(root.element + " ");
preOrder(root.left);
preOrder(root.right);
}
}
//后序遍历
public void postOrder(BinaryTreeNode<T> root) {
if (root != null) {
postOrder(root.left);
postOrder(root.right);
System.out.print(root.element + " ");
}
}contains,toString,方法均使用课本代码,其中toString是将PrintTree改名。
实验结果
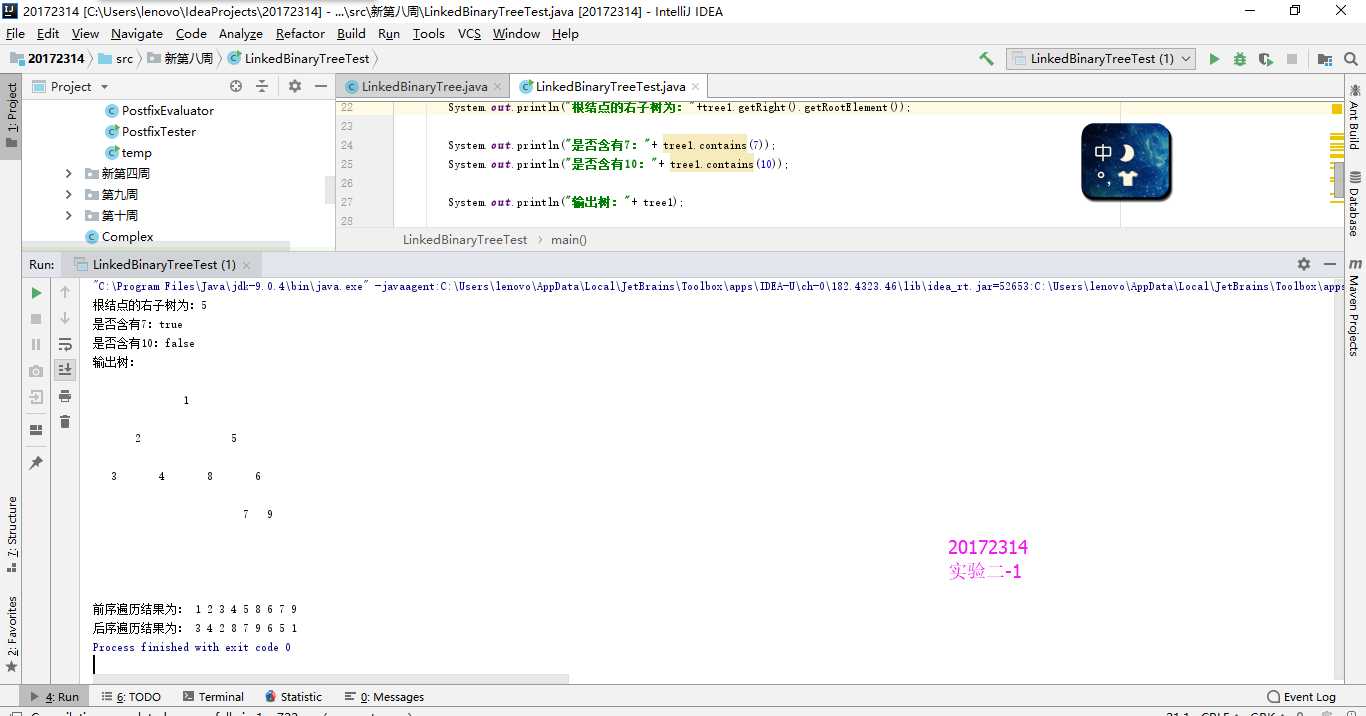
核心代码为:
public BinaryTreeNode<T> reBuildTree(String[] pre, String[] in, int preStart, int preEnd, int inStart, int inEnd) {
BinaryTreeNode root = new BinaryTreeNode(pre[preStart]);
root.left = null;
root.right = null;
if (preStart == preEnd && inStart == inEnd) {//只有一个元素时
return root;
}
int a = 0;
for(a= inStart; a < inEnd; a++){//找到中序遍历中根节点的位置
if (pre[preStart] == in[a]) {
break;
}
}
int leftLength = a - inStart;//找到左子树的元素个数
int rightLength = inEnd - a;//找到右子树的元素个数
if (leftLength > 0) {//左右子树分别进行以上操作
root.left= reBuildTree(pre, in, preStart+1, preStart+leftLength, inStart, a-1);
}
if (rightLength > 0) {
root.right = reBuildTree(pre, in, preStart+1+leftLength, preEnd, a+1, inEnd);
}
return root;
}最后使用
public void reBuildTree(String [] pre, String [] in) {
BinaryTreeNode a = reBuildTree(pre, in, 0, pre.length-1, 0, in.length-1);
root = a;
}实验结果
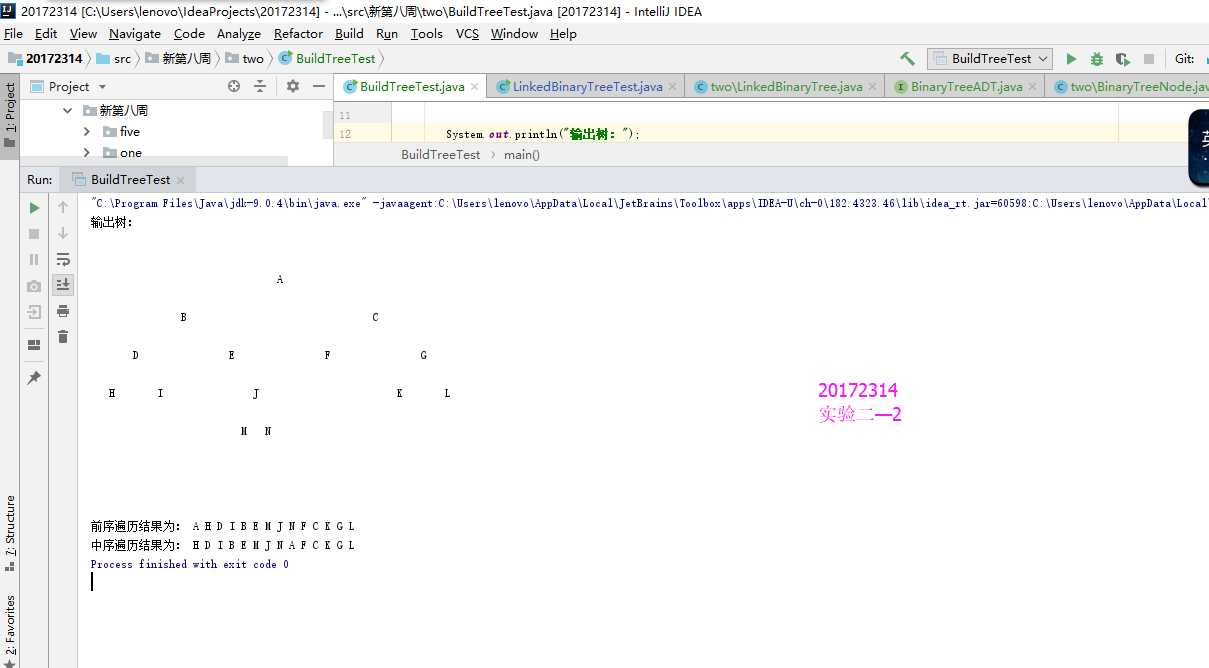
核心代码
public void evaluate() {
LinkedBinaryTree<String> current = tree;
Scanner scan = new Scanner(System.in);
while (current.size() > 1) {
System.out.println(current.getRootElement());
if (scan.nextLine().equalsIgnoreCase("N"))
current = current.getLeft();
else
current = current.getRight();
}
System.out.println("得出结论:"+current.getRootElement());
}实验结果
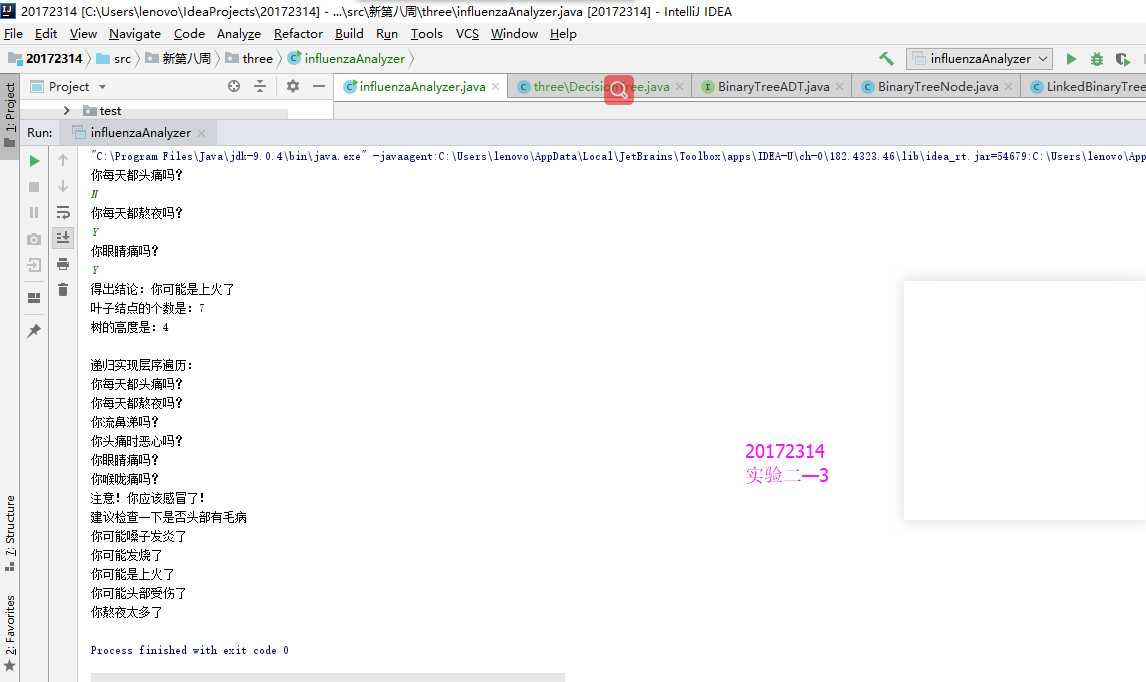
核心代码
public BinaryTreeNode BuildTree(String str) {
ArrayList<BinaryTreeNode> num = new ArrayList<BinaryTreeNode>();
ArrayList<String> symbol = new ArrayList<String>();
StringTokenizer st = new StringTokenizer(str); //得到输入的数字和符号
String next;
while (st.hasMoreTokens()) {
next = st.nextToken();
if (next.equals("(")) {
String str1 = "";
next = st.nextToken();
while (!next.equals(")")) {//计算括号内的内容,当找到右括号时,进行下面的步骤构造树
str1 += next + " ";
next = st.nextToken();
}
num.add(BuildTree(str1));//括号里的优先,创建一棵树
if (st.hasMoreTokens()) {
next = st.nextToken();
} else
break;
}
if (!next.equals("+") && !next.equals("-") && !next.equals("*") && !next.equals("/")) {
num.add(new BinaryTreeNode(next)); //是数字进入num
}
if (next.equals("+") || next.equals("-")) {
BinaryTreeNode<String> tempNode = new BinaryTreeNode<>(next);
next = st.nextToken();
if (!next.equals("(")) {
symbol.add(tempNode.element);//优先级低,存入符号集
num.add(new BinaryTreeNode(next));
}
else {
symbol.add(tempNode.element);
String temp = st.nextToken();
String s = "";
while (!temp.equals(")")) {//收集括号内的信息
s += temp + " ";
temp = st.nextToken();
}
num.add(BuildTree(s));//对括号内的建树
}
}
if (next.equals("*") || next.equals("/")) {
BinaryTreeNode<String> tempNode = new BinaryTreeNode<>(next);
next = st.nextToken();
if (!next.equals("(")) {//没有括号时,以* / 为父结点建树,num中最后两个数分别为左右孩子
tempNode.setLeft(num.remove(num.size() - 1));
tempNode.setRight(new BinaryTreeNode<String>(next));
num.add(tempNode);//将这个树添加到num中
} else { //遇到括号,num的最后一个数为左孩子,剩下的都是右子树
String temp = st.nextToken();
tempNode.setLeft(num.remove(num.size() - 1));//把* 或/ 前面的数变为左子树
String s = "";
while (!temp.equals(")")) {//括号中内容全部是的是右子树
s += temp + " ";
temp = st.nextToken();
}
tempNode.setRight(BuildTree(s));
num.add(tempNode);
}
}
}
int i = symbol.size();
while (i > 0) {//最后把num中存放的小树,整合成一棵完整的树。
BinaryTreeNode<T> root = new BinaryTreeNode(symbol.remove(symbol.size() - 1));
root.setRight(num.remove(num.size() - 1));
root.setLeft(num.remove(num.size() - 1));
num.add(root);
i--;
}
return num.get(0);//输出最终的树
}实验结果
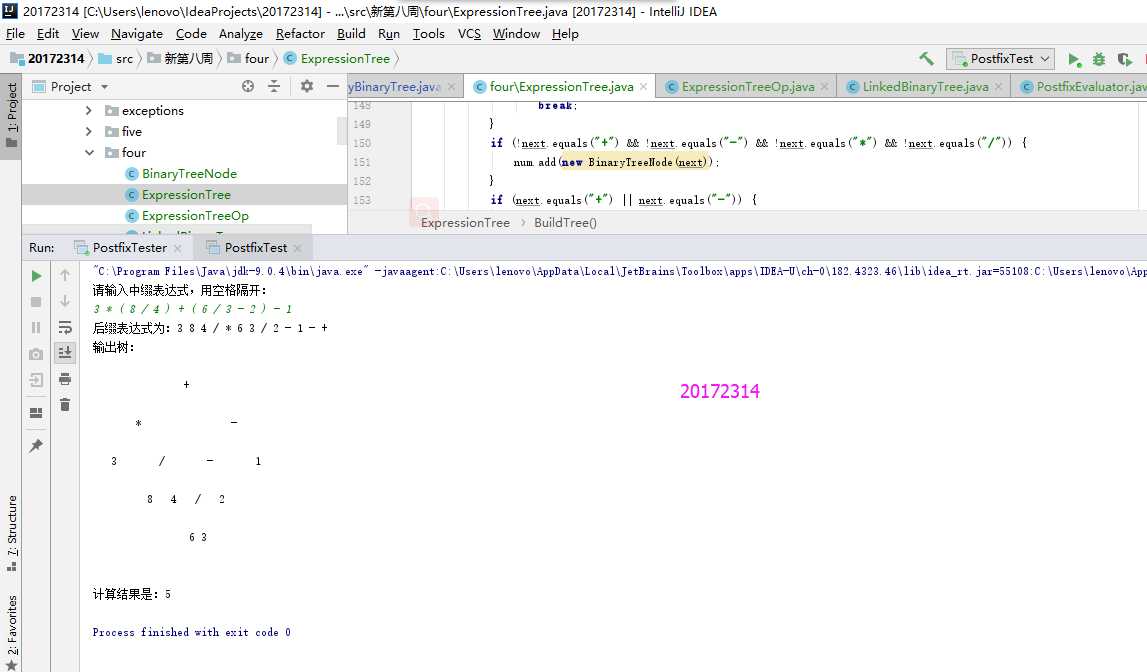
核心代码
public T findMin() {
T result = null;
if (isEmpty())
throw new EmptyCollectionException("LinkedBinarySearchTree");
else {
if (root.left == null) {
result = root.element;
//root = root.right;
} else {
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.left;
while (current.left != null) {
parent = current;
current = current.left;
}
result = current.element;
//parent.left = current.right;
}
//modCount--;
}
return result;
}@Override
public T findMax() {
T result = null;
if (isEmpty())
throw new EmptyCollectionException("LinkedBinarySearchTree");
else {
if (root.right == null) {
result = root.element;
//root = root.left;
} else {
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.right;
while (current.right != null) {
parent = current;
current = current.right;
}
result = current.element;
//parent.right = current.left;
}
//modCount--;
}
return result;
}public T removeMax() {
T result = null;
if (isEmpty())
throw new EmptyCollectionException("LinkedBinarySearchTree");
else {
if (root.right == null) {
result = root.element;
root = root.left;
} else {
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.right;
while (current.right != null) {//找右子树,他为最大
parent = current;
current = current.right;
}
result = current.element;//得到最大值
parent.right = current.left;//用左孩子替换最大的
}
modCount--;
}
return result;
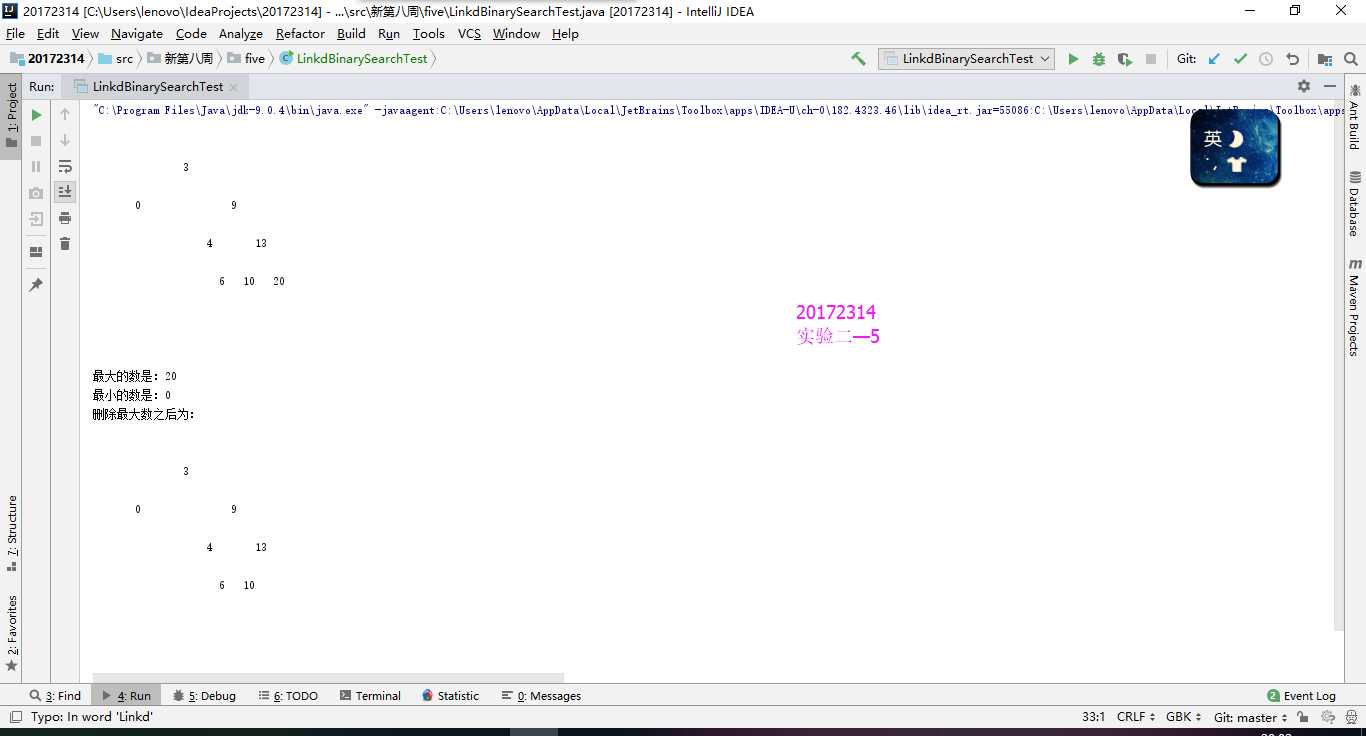
}findMin和findMax类似,removeMax是在findMax的基础上找到之后将其替换。由于二叉查找树左孩子小于根小于右孩子,例如findMin操作,当左孩子为空时,返回根结点(最小),否则向下查找到最后一个左孩子,返回其值。
实验结果
TreeMap类的继承关系
public class TreeMap<K,V> extends AbstractMap<K,V>implements NavigableMap<K,V>, Cloneable, SerializableTreeMap 是一个有序的key-value集合,它是通过红黑树实现的。
TreeMap 继承于AbstractMap,所以它是一个Map,即一个key-value集合。
TreeMap 实现了NavigableMap接口,意味着它支持一系列的导航方法。比如返回有序的key集合。
TreeMap 实现了Cloneable接口,意味着它能被克隆。
TreeMap 实现了java.io.Serializable接口,意味着它支持序列化。
TreeMap基于红黑树(Red-Blacktree)实现。该映射根据其键的自然顺序进行排序,或者根据创建映射时提供的 Comparator进行排序,具体取决于使用的构造方法。构造函数
// 默认构造函数
public TreeMap() {
comparator = null;
}
// 带比较器的构造函数
public TreeMap(Comparator<? super K> comparator) {
this.comparator = comparator;
}
// 带Map的构造函数,Map会成为TreeMap的子集
public TreeMap(Map<? extends K, ? extends V> m) {
comparator = null;
putAll(m);
}
// 带SortedMap的构造函数,SortedMap会成为TreeMap的子集
public TreeMap(SortedMap<K, ? extends V> m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}从TreeMap中删除第一个节点方法
public Map.Entry<K,V> pollFirstEntry() {
// 获取第一个节点
Entry<K,V> p = getFirstEntry();
Map.Entry<K,V> result = exportEntry(p);
// 删除第一个节点
if (p != null)
deleteEntry(p);
return result;
}返回小于key值的最大的键值对所对应的KEY,没有的话返回null
public K lowerKey(K key) {
return keyOrNull(getLowerEntry(key));
}获取Map的头部,范围从第一个节点 到 toKey.
public NavigableMap<K,V> headMap(K toKey, boolean inclusive) {
return new AscendingSubMap(this,
true, null, true,
false, toKey, inclusive);
}删除当前结点
需注意当lastReturned的左右孩子都不为空时,要将其赋值给next。是因为删除lastReturned节点之后,next节点指向的仍然是下一个节点。根据红黑树的特性可知:当被删除节点有两个儿子时。那么,首先把它的后继节点的内容复制给该节点的内容,之后删除它的后继节点。这意味着当被删除节点有两个儿子时,删除当前节点之后,新的当前节点实际上是原有的后继节点(即下一个节点)。而此时next仍然指向新的当前节点。也就是说next是仍然是指向下一个节点,能继续遍历红黑树。
public void remove() {
if (lastReturned == null)
throw new IllegalStateException();
if (modCount != expectedModCount)
throw new ConcurrentModificationException();
if (lastReturned.left != null && lastReturned.right != null)
next = lastReturned;
deleteEntry(lastReturned);
expectedModCount = modCount;
lastReturned = null;
}
}firstEntry()和getFirstEntry()
public Map.Entry<K,V> firstEntry() {
return exportEntry(getFirstEntry());
}
final Entry<K,V> getFirstEntry() {
Entry<K,V> p = root;
if (p != null)
while (p.left != null)
p = p.left;
return p;
}firstEntry()和getFirstEntry()都是用于获取第一个节点,firstEntry()是对外接口;getFirstEntry() 是内部接口。而且,firstEntry()是通过getFirstEntry() 来实现的。之所以不直接调用getFirstEntry()是为了防止用户修改返回的Entry。我们可以调用Entry的getKey()、getValue()来获取key和value值,以及调用setValue()来修改value的值,而对firstEntry()返回的Entry对象只能进行getKey()、getValue()等读取操作。所以要调用 firstEntry()获取。
HashMap
HashMap由数组+链表组成的,数组是HashMap的主体,链表则是主要为了解决哈希冲突而存在的,如果定位到的数组位置不含链表(当前entry的next指向null),那么对于查找,添加等操作很快,仅需一次寻址即可;如果定位到的数组包含链表,对于添加操作,其时间复杂度为O(n),首先遍历链表,存在即覆盖,否则新增,对于查找操作来讲,仍需遍历链表,然后通过key对象的equals方法逐一比对查找。所以,性能考虑,HashMap中的链表出现越少,性能才会越好。
get方法
get方法通过key值返回对应value,如果key为null,直接去table[0]处检索
public V get(Object key) {//如果key为null,则直接去table[0]处去检索即可。
if (key == null)
return getForNullKey();
Entry<K,V> entry = getEntry(key);
return null == entry ? null : entry.getValue();
}getEntry方法
get方法的实现相对简单,key(hashcode)-->hash-->indexFor-->最终索引位置,找到对应位置table[i],再查看是否有链表,遍历链表,通过key的equals方法比对查找对应的记录。要注意的是,上面在定位到数组位置之后然后遍历链表的时候,e.hash==hash是有必要的,不能仅通过equals判断。因为如果传入的key对象重写了equals方法却没有重写hashCode,而恰巧此对象定位到这个数组位置,如果仅仅用equals判断可能是相等的,但其hashCode和当前对象不一致,这种情况,根据Object的hashCode的约定,不能返回当前对象,而应该返回null。
final Entry<K,V> getEntry(Object key) {
if (size == 0) {
return null;
}
//通过key的hashcode值计算hash值
int hash = (key == null) ? 0 : hash(key);
//indexFor (hash&length-1) 获取最终数组索引,然后遍历链表,通过equals方法比对找出对应记录
for (Entry<K,V> e = table[indexFor(hash, table.length)];
e != null;
e = e.next) {
Object k;
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
}
return null;
}roundUpToPowerOf2方法
这个处理使得数组长度一定为2的次幂,Integer.highestOneBit是用来获取最左边的bit(其他bit位为0)所代表的数值。
private static int roundUpToPowerOf2(int number) {
// assert number >= 0 : "number must be non-negative";
return number >= MAXIMUM_CAPACITY
? MAXIMUM_CAPACITY
: (number > 1) ? Integer.highestOneBit((number - 1) << 1) : 1;
}那么为什么数组长度一定是2的次幂呢?
这样会保证低位全为1,而扩容后只有一位差异,也就是多出了最左位的1,这样在通过 h&(length-1)的时候,只要h对应的最左边的那一个差异位为0,就能保证得到的新的数组索引和老数组索引一致,同时,数组长度保持2的次幂,length-1的低位都为1,会使得获得的数组索引index更加均匀,如果不是2的次幂,也就是低位不是全为1此时,h的低位部分不再具有唯一性了,哈希冲突的几率会变的更大。
问题一解决:前序序列可以确定根结点,由循环得出
for(a= inStart; a < inEnd; a++){//找到中序遍历中根节点的位置
if (pre[preStart] == in[a]) {
break;
}
}那么在中序序列中,根结点左右的元素即可确立,确定左右元素的数目leftLength和rightLength,若大于0,则分别进行
root.left= reBuildTree(pre, in, preStart+1, preStart+leftLength, inStart, a-1);
和
root.right = reBuildTree(pre, in, preStart+1+leftLength, preEnd, a+1, inEnd);
再次确定左右子树的根结点,如此循环,直到所有的结点被确定,这时树就形成了。
这次的实验报告有一点难度,花费挺长时间的,不过对树的了解更加深入了,学习到很多。
标签:分享 min() 教材 map接口 创建 tle 构造方法 htm sky
原文地址:https://www.cnblogs.com/YiYiYi/p/9940896.html