标签:输入 ros 特征 auto files 指定 结束 事先 .com
单层感知器属于单层前向网络,即除输入层和输出层之外,只拥有一层神经元节点。
特点:输入数据从输入层经过隐藏层向输出层逐层传播,相邻两层的神经元之间相互连接,同一层的神经元之间没有连接。
感知器(perception)是由美国学者F.Rosenblatt提出的。与最早提出的MP模型不同,神经元突触权值可变,因此可以通过一定规则进行学习。可以快速、可靠地解决线性可分的问题。
单层感知器由一个线性组合器和一个二值阈值元件组成。输入向量的各个分量先与权值相乘,然后在线性组合器中进行叠加,得到一个标量结果,其输出是线性组合结果经过一个二值阈值函数。二值阈值元件通常是一个上升函数,典型功能是非负数映射为1,负数映射为0或负一。
输入是一个N维向量 x=[x1,x2,...,xn],其中每一个分量对应一个权值wi,隐含层输出叠加为一个标量值:
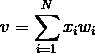
随后在二值阈值元件中对得到的v值进行判断,产生二值输出:
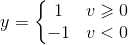
可以将数据分为两类。实际应用中,还加入偏置,值恒为1,权值为b。这时,y输出为:
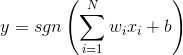
把偏置值当作特殊权值:

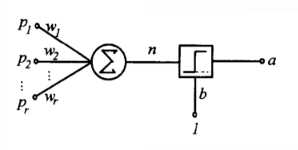
单层感知器结构图:
单层感知器进行模式识别的超平面由下式决定:
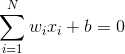
当维数N=2时,输入向量可以表示为平面直角坐标系中的一个点。此时分类超平面是一条直线:
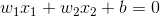
这样就可以将点沿直线划分成两类。
(1)定义变量和参数,这里的n是迭代次数。N是N维输入,将其中的偏置也作为输入,不过其值恒为1,。
x(n)=N+1维输入向量=[+1,x1(n),x2(n),...,xN(n)]T
w(n)=N+1维权值向量=[b(n),w1(n),w2(n),...,wN(n)]T
b(n)=偏置
y(n)=实际输出
d(n)=期望输出
η(n)=学习率参数,是一个比1小的正常数
所以线性组合器的输出为:v(n)=wT(n)x(n)
(2)初始化。n=0,将权值向量w设置为随机值或全零值。
(3)激活。输入训练样本,对每个训练样本x(n)=[+1,x1(n),x2(n),...,xN(n)]T,指定其期望输出d。即若x属于l1,则d=1,若x属于l2,则d属于-1(或者0)。
(4)计算实际输出。 y(n)=sgn(wT(n)x(n))
(5)更新权值向量 w(n+1)=w(n)+η[d(n)-y(n)]x(n)
感知器的学习规则:学习信号等于神经元期望输出与实际输出之差:

dj为期望的输出,oj为实际的输出。
W代表特征向量或者是矩阵。T代表矩阵的转置,X为输入信号或者是训练数据集中的一个m维样本


公式右侧前面的符号η为学习率。权值调整值为学习率乘以误差乘以输入信号(X)。
当实际输出与期望值相同时,权值不需要调整,在有误差存在的情况下,并且期望值与实际输出值为1或者-1,此时权值调整公式可以简化为:

每一次带入一个数据进行迭代,而不是带入所有数据(为什么呢,感觉带入所有数据进行运算会好很多)
这里
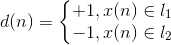
0<η<1
为什么权值更新会是这样呢:我认为可以这样理解,当y与d相同时,分类正确,权值不用更新。
当y与d不同时 : w(n+1)*x(n)=w(n)*x(n)+η[d(n)-y(n)]x(n)*x(n) 即当d为1而y为-1时,整体的w(n+1)*x(n)增加的,当d为-1而y为1时,整体是往-1的方向变化的,所以w(n+1)权值会使得整体往正确的分类走。但是这个权值更新公式怎么来的就还不知道了。
(6)判断。若满足收敛条件,则算法结束,若不满足,n++,转到第(3)步。
收敛条件:当权值向量w已经能正确实现分类时,算法就收敛了,此时网络误差为零。收敛条件通常可以是:
误差小于某个预先设定的较小的值ε。即
|d(n)-y(n)|<ε
两次迭代之间的权值变化已经很小,即
|w(n+1)-w(n)|<ε
为防止偶然因素导致的提取收敛,前两个条件还可以改进为连续若干次误差或者权值变化小于某个值。
设定最大迭代次数M,当迭代了M次就停止迭代。
需事先通过经验设定学习率η,不应该过大,以便为输入向量提供一个比较稳定的权值估计。不应过小,以便使权值能根据输入的向量x实时变化,体现误差对权值的修正作用。
它只对线性可分的问题收敛,通过学习调整权值,最终找到合适的决策面,实现正确分类。
单层感知器在研究线性不可分的问题中:可以追求尽量正确的分类,定义一个误差准则,在不同的超平面中选择一个最优超平面,,使得误差最小,实现近似分类。
标签:输入 ros 特征 auto files 指定 结束 事先 .com
原文地址:https://www.cnblogs.com/pythonlearing/p/9947051.html