标签:压缩 输入 网络 依据 放大 研究 世纪 阶段 back
BP神经网络是包含多个隐含层的网络,具备处理线性不可分问题的能力。以往主要是没有适合多层神经网络的学习算法,,所以神经网络的研究一直处于低迷期。
20世纪80年代中期,Rumelhart,McClelland等成立了Parallel Distributed Procession(PDP)小组,提出了著名的误差反向传播算法(Error Back Propagtion,BP)。
BP和径向基网络属于多层前向神经网络。广泛应用于分类识别、逼近、回归、压缩等领域。
BP神经网络(强调是用BP算法)一般是多层的,其概念和多层感知器(强调多层)差不多是等价的,隐层可以是一层或多层。BP神经网络具有如下特点:
(1)网络由多层构成,层与层之间全连接,同一层之间的神经元无连接。
(2)BP网络的传递函数必须可微。所以感知器的二值函数不能用,一般采用Sigmoid函数,可分为Log-Sigmoid和Tan-Sigmoid函数。
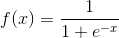
其中x的范围包含整个实数域,函数值再0~1之间。具体应用时可以增加参数,以控制曲线的位置和形状。
sigmoid函数可以将输入从负无穷到正无穷的范围映射到(-1,1)和(0,1)之间,在原点处具有非线性放大功能。BP的典型设计是隐含层采用Sigmoid函数作为传递函数,输出层采用线性函数作为传递函数。(一定不能全部层都采用线性的,否则就会和线性神经网络一样了)
(3)采用误差反向传播算法(Back-Propagation)进行学习。再BP网络中,数据从输入层经隐含层逐层向后传播,训练网络权值时,则沿着减少误差的方向,从输出层经过中间各层逐层向前修正网络连接权值。
(与反馈神经网络不同,BP是误差信号反向传播,网络根据误差从后向前逐层进行修正)
(1)网络由多层构成,层与层之间全连接,同一层之间的神经元无连接。
(2)BP网络的传递函数必须可微。所以感知器的二值函数不能用,一般采用Sigmoid函数,可分为Log-Sigmoid和Tan-Sigmoid函数。
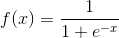
其中x的范围包含整个实数域,函数值再0~1之间。具体应用时可以增加参数,以控制曲线的位置和形状。
sigmoid函数可以将输入从负无穷到正无穷的范围映射到(-1,1)和(0,1)之间,具有非线性放大功能。
(3)采用误差反向传播算法(Back-Propagation)进行学习。再BP网络中,数据从输入层经隐含层逐层向后传播,训练网络权值时,则沿着减少误差的方向,从输出层经过中间各层逐层向前修正网络连接权值。
(与反馈神经网络不同,BP是误差信号反向传播,网络根据误差从后向前逐层进行修正)
(1)网络由多层构成,层与层之间全连接,同一层之间的神经元无连接。
(2)BP网络的传递函数必须可微。所以感知器的二值函数不能用,一般采用Sigmoid函数,可分为Log-Sigmoid和Tan-Sigmoid函数。
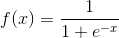
其中x的范围包含整个实数域,函数值再0~1之间。具体应用时可以增加参数,以控制曲线的位置和形状。
sigmoid函数可以将输入从负无穷到正无穷的范围映射到(-1,1)和(0,1)之间,具有非线性放大功能。
(3)采用误差反向传播算法(Back-Propagation)进行学习。再BP网络中,数据从输入层经隐含层逐层向后传播,训练网络权值时,则沿着减少误差的方向,从输出层经过中间各层逐层向前修正网络连接权值。
(与反馈神经网络不同,BP是误差信号反向传播,网络根据误差从后向前逐层进行修正)
BP算法的基本思想是,学习过程由信号的正向传播和误差的反向传播俩个过程组成,输入从输入层输入,经隐层处理以后,传向输出层。如果输出层的实际输出和期望输出不符合,就进入误差的反向传播阶段。误差反向传播是将输出误差以某种形式通过隐层向输入层反向传播,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,这个误差信号就作为修正个单元权值的依据。直到输出的误差满足一定条件或者迭代次数达到一定次数。
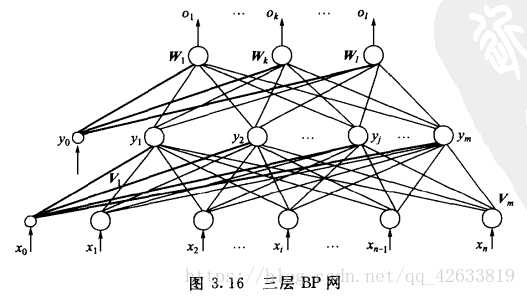
使用的传递函数sigmoid可微的特性使他可以使用梯度下降法。所以,在隐层函数中使用sigmoid函数作为传递函数,在输出层采用线性函数作为传递函数。
输入向量、隐层输出向量、最终输出向量、期望输出向量:
X=(x0,x1,x2,x3……xn),其中图中x0是为隐层神经元引入阈值设置的;x0=1
Y=(y0,y1,y2,y3……ym),其中图中y0是为输出神经元引入阈值设置的;y0=1
O=(o1,o2,o3……ol)
D=(d1,d2,d3……dl)
输出层的输入是隐层的输出,隐层的输入是输入层的输出,计算方法和单层感知器的计算方法一样。
确定层数和每层的神经元个数后,还需直到权值系数才能由输入给出正确的输出。
BP网络的学习属于有监督学习,需要一组已知目标输出的学习样本集。
先使用随机值作为权值,得到网络输出之后与期望输出作对比,然后根据输出值与期望值的计算误差,再由误差根据某种准则逐层修改权值,使得误差减小。
标签:压缩 输入 网络 依据 放大 研究 世纪 阶段 back
原文地址:https://www.cnblogs.com/pythonlearing/p/9949415.html