标签：情况 图片 min 简单 noi main algorithm alt names
题意：在一个岛上，有n个野人。这些人开始住在c号洞穴，每一年走p个洞，而且他的生命有L年.问如果岛上的洞穴为一个圈，那么这个圈至少有多少个，才能使他们每年都不在同一个洞穴里。
分析：先假设一种简单的情况！假设有2个人。
第一个人：c：1， p：2 ，L=3
第二个人：c: 2, p: 3, L=4
假如：一共有8个洞：如图：
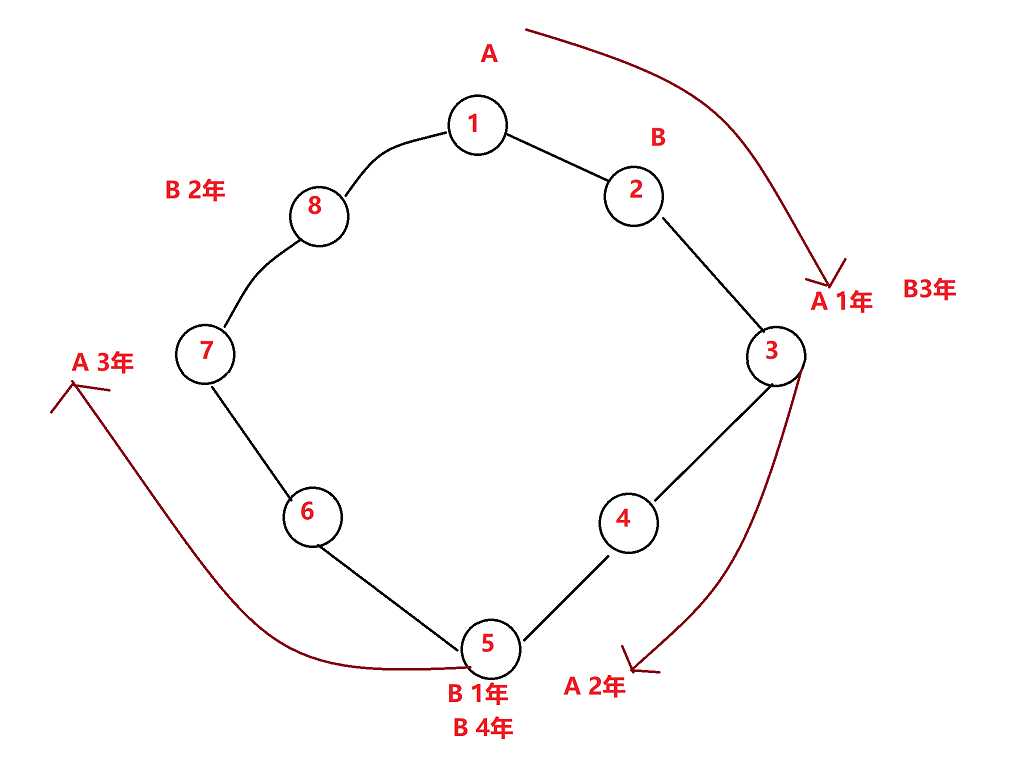这样就能保证。
数学知识：欧几里得拓展
不定方程ax+by=c,由
得，若x，y有整数x解（正负无所谓，但是注意正数解，在mod运算中）则， c能被gcd（a， b）;
分析：如果，有两个野人在某一个洞穴相遇，则表明 （p1-p2）x+by=c1-c2; 有解。但是，如果他的最小整数解都小于两个野人的寿命，则也可以。
那么，就是在枚举一共有多少山洞，然后判断是否满足。第一个满足的就是最小的洞数。
#include<cstdio> #include<iostream> #include<cmath> #include<algorithm> using namespace std; int c[20], p[20], L[20]; int n; int gcd(int a, int b){ return b == 0 ? a : gcd(b, a%b); } void exgcd(int a, int b, int &x, int &y){ if (b == 0){ x = 1; y = 0; return; } exgcd(b, a%b, x, y); int t = x; x = y; y = t - a / b*y; } bool fun(int m){ int x, y, A, B, C, t; for (int i = 1; i <= n; ++i) for (int j = i + 1; j <= n; ++j){ A = p[i] - p[j]; B = m; C = c[j] - c[i]; t = gcd(A, B); if (C%t == 0){ A /= t; B /= t; C /= t; exgcd(A, B, x, y); B = abs(B); x = ((C*x) % B + B) % B; if (x <= min(L[i], L[j]))return 0; } } return 1; } int main() { int maxn = 0; scanf("%d", &n); for (int i = 1; i <= n; ++i){ scanf("%d%d%d", &c[i], &p[i], &L[i]); maxn = max(maxn, c[i]); } for (int i = maxn;; ++i){ if (fun(i)){ printf("%d\n", i); return 0; } } }
标签：情况 图片 min 简单 noi main algorithm alt names
原文地址：https://www.cnblogs.com/ALINGMAOMAO/p/9955473.html
