标签：推广 连续 get EDA db2 idt 分享图片 就是 ali
在概率论和统计学中，数学期望是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。
离散型随机变量X的取值为
， 
为X对应取值的概率，可理解为数据 出现的频率
，则：
为随机变量的数学期望，记为E(X)。 
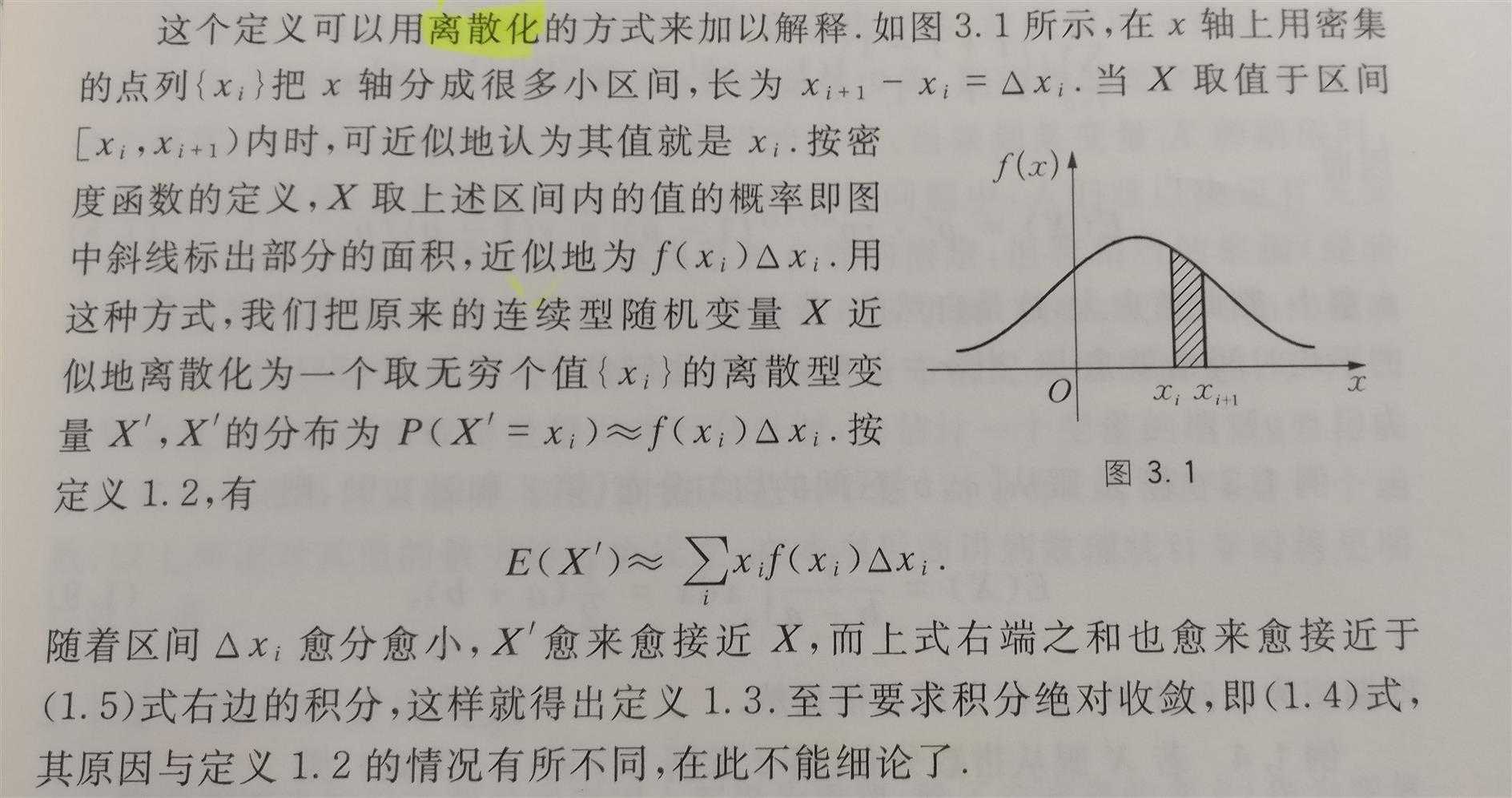
数学期望是由随机变量的分布完全决定的，故我们常说某分布F的期望是多少，或某密度f的密度是多少。
数学期望之所以在理论和应用上都极为重要，除了它本身的含义(作为变量平均取值的刻画)外，还有 一个原因，即它具有一些良好的性质,这些性质使得它在数学上很方便。
若随机变量Y符合函数
，且
绝对收敛，则有：
该定理的意义在于：我们求 
时不需要算出Y的分布律或者概率密度，只要利用X的分布律或概率密度即可。
方差之所以成为刻画散布度的最重要的数字特征，原因之一就是它具有一些优良的数学性质：
标签：推广 连续 get EDA db2 idt 分享图片 就是 ali
原文地址：https://www.cnblogs.com/zxygenesis/p/9955605.html
