标签：缘分   http   添加   src   字典   目标   ecif   提取   begin   

1. 简介

寻找领域不变特征一般分为三类：

• 子空间学习
• 非线性投影
• [X] 字典学习
  • 稀疏约束
  • [X] 低秩约束
  • 局部约束

为了实现两个领域的迁移需要减小其分布差异：

• [X] 边缘分布\(P(X_{s})\)与\(P(X_{t})\)
• [X] 条件分布\(P(Y_{s} \mid X_{s})\)与\(P(Y_{t} \mid X_{t})\)

2. 详情

1. 从稀疏编码谈起：

   \[ \underset{D,Z}{min} \quad \lVert {X-DZ}\rVert_{F}^{2} + \mathcal{N}(Z) \ s.t. \,\, \lVert{{d}_{i}^j}\rVert_{2}^2 \le 1 \quad \forall i,j \]

2. 减小边缘分布差异：

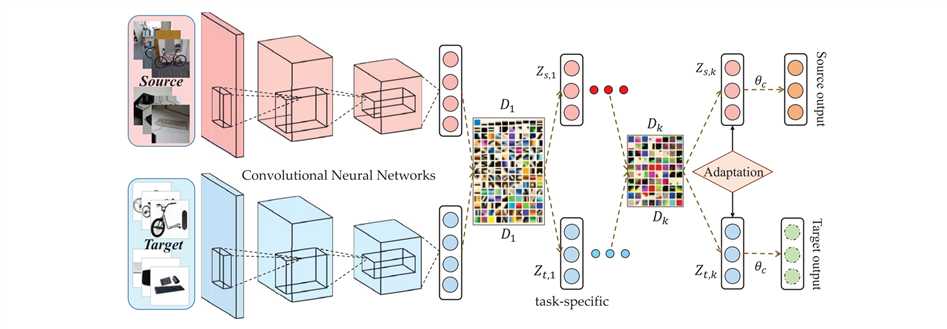
   1. 由于光照，角度等问题。直接通过字典学习得到新特征太浅显。\(\Rightarrow\)使用CNN提取抽象特征（参数共享）。

   2. 对于存在较大分布差异情况，学习的一个字典之后\(P(Z_{s})\)与\(P(Z_{t})\)间差异依然大。\(\Rightarrow\)通过task-specific全连接层学习多层字典来覆盖两个领域共同特征，逐步减小分布差异。
      • task-specific全连接层的神经元个数需要根据秩固定。
   3. \(\Rightarrow\)通过对\(Z\)的低秩约束来获取有识别力的新特征。（还能防止过拟合）
      • 只需约束最后一层的\(Z_{k}\)就能使中间层都能低秩学习：

      \[ \left. \begin{aligned} Z_{k-1} = D_{k}Z_{k} \Rightarrow \text{rank}(Z_{k-1}) = \text{rank}(D_{k}Z_{k}) \ \text{rank}(D_{k}Z_{k}) \le min(\text{rank}(Z_{k}),\text{rank}(D_{k})) \end{aligned} \right\} \Rightarrow \text{rank}(Z_{k-1}) \le \text{rank}(Z_{k}) \ \Downarrow \\ \text{rank}(Z_{1}) \le \text{rank}(Z_{2}) \le \cdots \text{rank}(Z_{k}) \]

   4. 改进结果：

   \[ \underset{D_{1}\dots,D_{2},Z_{k}}{min} \quad \lVert{X-D_{1}D_{2}\dots D_{k}Z_{k}}\rVert_{F}^{2} + \text{rank}(Z_{k}) \ s.t. \,\, \lVert{{d}_{i}^j}\rVert_{2}^2 \le 1 \quad \forall i,j \]

3. 减小条件分布差异：

   • 半监督知识适应(\(Z_{k}=[Z_{k}^s,Z_{k}^t]\))：

     1. 从传统的MMD谈起：

     \[ \mathcal{M}(Z_{k}) = \Vert {\frac{1}{m_{s}} \sum_{i=1}^{m_{s}} {z_{k,i}} - \frac{1}{m_{t}} \sum_{j=m_{s}+1}^{m}{z_{k,j}} } \Vert_{2}^2 = \sum_{i=1}^m \sum_{j=1}^m {z_{k,i}^\top z_{k,j}W_{ij}=\text{tr}(Z_{k}WZ_{k}^\top)} \]

     1. 改进：

        1. 传统的MMD只能减小边缘分布差异\(\Rightarrow\)采用类间MMD，可减小条件分布差异。

        2. 但目标域几乎无标签可用\(\Rightarrow\)对目标域样本添加"soft label"。

     \[ \mathcal{C}(Z_{k}) = \sum_{c=1}^C \Vert {\frac{1}{m_{s}^c} \sum_{i=1}^{m_{s}^c} {z_{k,i}^{s}} - \frac{1}{m_{t}^c} \sum_{j=1}^{m_{t}}{p_{c,j}z_{k,j}^{t}} } \Vert_{2}^2 = \sum_{c=1}^C \text{tr}(Z_{k}W^{(c)}Z_{k}^\top) \]

4. "end-to-end"：

   • 添加softmax层，计算交叉熵损失，引导类内特征相似：

   \[ \mathcal{J}(Z_{K},\Theta,Y) = -\frac{1}{m}\sum _{i=1}^m \sum_{c=1}^C y_{c,i}\text{log}\frac{e^{\theta_{c}^\top}z_{k,i}}{\sum_{u=1}^C e^{\theta_{u}^\top}z_{k,i}} \]

5. 非线性化：

   • 非线性的数据表示可有效减少统计和感知冗余，使用ReLU这个非线性的激活函数：

   \[ Z_{i} \approx f(D_{i+1}Z_{i+1}) \]

6. 最终目标函数:

   \[ \mathcal{L} = \mathcal{L}(Z_{k},\Theta,Y) + \lambda\Vert{X-D_{1}f(D_{2}f(\cdots f(D_{k}Z_{k}) ))}\Vert_{F}^2 +\alpha\sum_{c=0}^C\text{tr}(Z_{k}W^{(c)}Z_{k}^{\top})+\beta\Vert{Z_{k}-AB}\Vert_{F}^2 \]

3. 启发

1. 充分发挥各类神经网络的特点。CNN提取抽象特征，NN非线性拟合，GAN拟合分布，RNN序列模型。

Paper Notes (1)

标签：缘分   http   添加   src   字典   目标   ecif   提取   begin   

原文地址：https://www.cnblogs.com/YvanZh/p/9960280.html