标签:rac 数组 ack com tps 框架 void element 处理
二进制手表顶部有 4 个 LED 代表小时(0-11),底部的 6 个 LED 代表分钟(0-59)。
每个 LED 代表一个 0 或 1,最低位在右侧。

例如,上面的二进制手表读取 “3:25”。
给定一个非负整数 n 代表当前 LED 亮着的数量,返回所有可能的时间。
案例:
输入: n = 1 返回: ["1:00", "2:00", "4:00", "8:00", "0:01", "0:02", "0:04", "0:08", "0:16", "0:32"]
注意事项:
这道题目标注为简单题,但感觉做起来比较费劲,虽然最后写出来了,但感觉代码很冗余。讨论有很多非常巧妙的办法,需要运用数学方法,我是绝对想不出来的。
我的思路是这样的,题目意思是在小时数组{1,2,4,8} 和分钟数组{1,2,4,8,16,32}中一共选择N个数来组成一个时间。
那我们第一个要解决的问题是如何在一个数组中选出所有N个数的组合。
1、如何取出组合的第一个数?
我们从左往右,首先我们将a加入tmpList(临时存储排列的线性表)中,此后再从它下一个位置开始找第二个、第三个数字,最后生成排列存储在结果中。我们再将1作为第一个元素开始处理后,赶紧把他删了,再将b加入到tmpList中,此后再从它下一个位置开始找第二个、第三个数字,最后生成排列存储在结果中....
也就是说处理第i个位置的元素时,就要考虑到i位置的所有取值,我们在处理为a的元素后,赶紧把他删了处理为b的元素.....这样第i个位置就有所有的情况了。
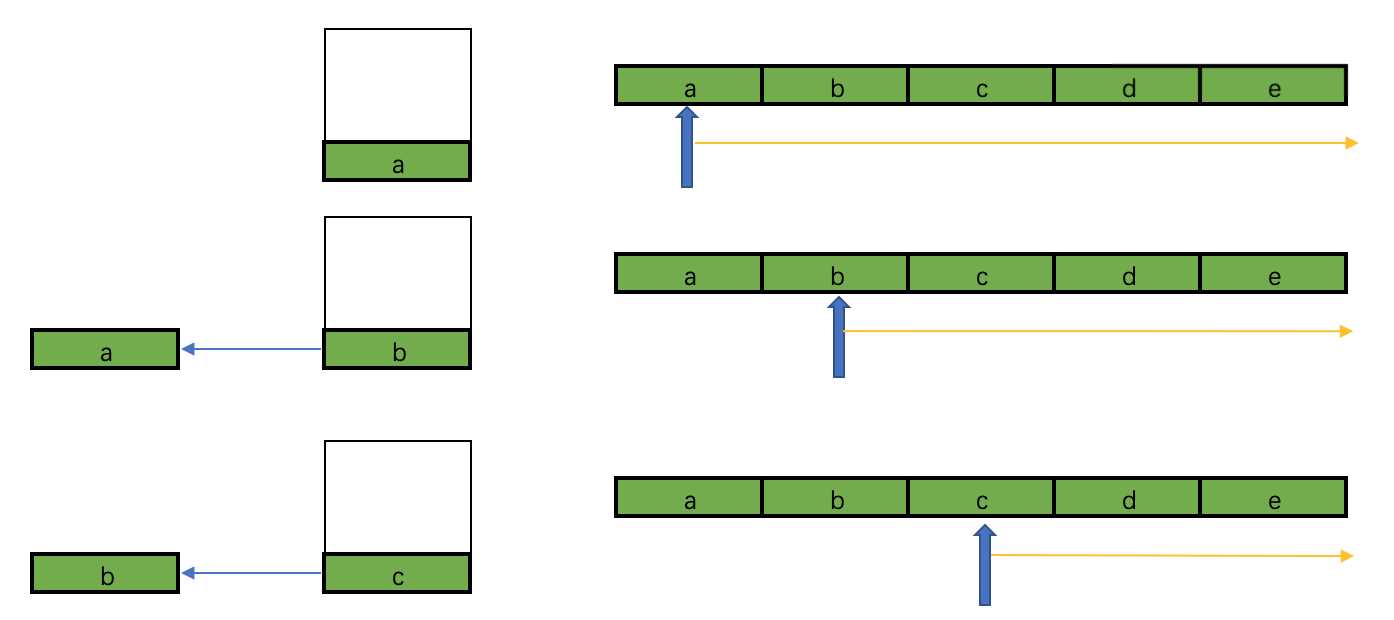
知道这个以后,我们就可以得到在一个数组中选出所有N个数的组合。
2、关于排列组合的一个典型的递归回溯框架是这样的
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums){
if(tempList.size() == nums.length){
list.add(new ArrayList<>(tempList));
} else{
for(int i = 0; i < nums.length; i++){
if(tempList.contains(nums[i])) continue; // element already exists, skip
tempList.add(nums[i]);
backtrack(list, tempList, nums);
tempList.remove(tempList.size() - 1);
}
}
}
当我们分别取出小时和分钟的各种可能情况,再次做他们的笛卡尔积,从而生产所有的时间可能。
很抱歉的是,这道题并不需要严格的递归回溯框架,我从而使用了简单使用了深搜。
/**
*
* @param arr 待产生排列的数组
* @param index 位置下标
* @param cur 已经找了CUR个数
* @param n 一共要找N个数
* @param val 已经找到的数的和
* @param res 当招够N个数后把他加入res表中
* @param max val不能超过多少
*/
private void helper(int[] arr,int index,int cur,int n,int val,List<Integer> res,int max)
{
if(cur>n)
return;
if(cur==n&&val<max)
res.add(val);
for(int i =index;i<arr.length;i++) {
helper(arr, i+1,cur+1, n, val + arr[i],res,max);
}
}
class Solution {
public List<String> readBinaryWatch(int num) {
int[] hour = {1,2,4,8};
int[] minute ={1,2,4,8,16,32};
List<Integer> hourList = new ArrayList<>();
List<Integer> minuteList = new ArrayList<>();
List<String> ans = new ArrayList<>();
for(int i=0;i<=num;i++)
{
helper(hour,0,0,i,0,hourList,12);
helper(minute,0,0,num-i,0,minuteList,60);
for(int hi = 0;hi<hourList.size();hi++)
for(int mi =0;mi<minuteList.size();mi++)
{
String minVal = String.valueOf(minuteList.get(mi));
if(minVal.length()<2)
minVal = "0"+minVal;
ans.add(hourList.get(hi)+":"+minVal);
}
hourList = new ArrayList<>();
minuteList = new ArrayList<>();
}
Collections.sort(ans);
return ans;
}
private void helper(int[] arr,int index,int cur,int n,int val,List<Integer> res,int max)
{
if(cur>n)
return;
if(cur==n&&val<max)
res.add(val);
for(int i =index;i<arr.length;i++) {
helper(arr, i+1,cur+1, n, val + arr[i],res,max);
}
}
}
标签:rac 数组 ack com tps 框架 void element 处理
原文地址:https://www.cnblogs.com/MrSaver/p/9962717.html