标签:pearson rds target ati 机器 数据挖掘 bsp 缺陷 需要
俗话说的好,不动手就永远不知道该怎么做,上次一听说要做这个的时候人都懵了,听了几次似乎都摸不到门道,这次花了几天时间去写了写,总算是摸到了点门道。
这次用到的数据集是跟火电厂有关的,都是匿名特征,数据量为20160*170,做到最后发现只根据时间顺序就能做的比较好。
先来讲讲归一化。归一化也称标准化,是数据挖掘的一项基础工作,使用归一化的原因大体如下
线性归一化,也称为离差标准化,是对原始数据的线性变换,min-max标准化方法的缺陷在当有新数据加入时,可能会导致X.max和X.min的值发生变化,需要重新计算。其转换函数如下:
标准差归一化,也叫Z-score标准化,这种方法给予原始数据的均值(mean,μ)和标准差(standard deviation,σ)进行数据的标准化。经过处理后的数据符合标准正态分布,即均值为0,标准差为1,转化函数为:
原理与MinMaxScaler很像,只是数据会被规模化到[-1,1]之间。也就是特征中,所有数据都会除以最大值。这个方法对那些已经中心化均值维0或者稀疏的数据有意义。
本次实验使用了5个模型,分别为Lasso、Redige、SVR、RandomForest、XGBoost。
数据预处理
#按时间排序 sort_data = data.sort_values(by = ‘time‘,ascending = True) sort_data.reset_index(inplace = True,drop = True) target = data[‘T1AOMW_AV‘] sort_target = sort_data[‘T1AOMW_AV‘] del data[‘T1AOMW_AV‘] del sort_data[‘T1AOMW_AV‘] from sklearn.model_selection import train_test_split test_sort_data = sort_data[16160:] test_sort_target = sort_target[16160:] _sort_data = sort_data[:16160] _sort_target = sort_target[:16160] sort_data1 = _sort_data[:(int)(len(_sort_data)*0.75)] sort_data2 = _sort_data[(int)(len(_sort_data)*0.75):] sort_target1 = _sort_target[:(int)(len(_sort_target)*0.75)] sort_target2 = _sort_target[(int)(len(_sort_target)*0.75):] import scipy.stats as stats dict_corr = { ‘spearman‘ : [], ‘pearson‘ : [], ‘kendall‘ : [], ‘columns‘ : [] } for i in data.columns: corr_pear,pval = stats.pearsonr(sort_data[i],sort_target) corr_spear,pval = stats.spearmanr(sort_data[i],sort_target) corr_kendall,pval = stats.kendalltau(sort_data[i],sort_target) dict_corr[‘pearson‘].append(abs(corr_pear)) dict_corr[‘spearman‘].append(abs(corr_spear)) dict_corr[‘kendall‘].append(abs(corr_kendall)) dict_corr[‘columns‘].append(i) # 筛选新属性 dict_corr =pd.DataFrame(dict_corr) new_fea = list(dict_corr[(dict_corr[‘pearson‘]>0.41) & (dict_corr[‘spearman‘]>0.45) & (dict_corr[‘kendall‘]>0.29)][‘columns‘].values) # 选取原则,选取25%分位数 以上的相关性系数
模型测试
from sklearn.linear_model import LinearRegression,Lasso,Ridge from sklearn.preprocessing import MinMaxScaler,StandardScaler,MaxAbsScaler from sklearn.metrics import mean_squared_error as mse from sklearn.svm import SVR from sklearn.ensemble import RandomForestRegressor import xgboost as xgb #最大最小归一化 mm = MinMaxScaler() lr = Lasso(alpha=0.5) lr.fit(mm.fit_transform(sort_data1[new_fea]), sort_target1) lr_ans = lr.predict(mm.transform(sort_data2[new_fea])) print(‘lr:‘,mse(lr_ans,sort_target2)) ridge = Ridge(alpha=0.5) ridge.fit(mm.fit_transform(sort_data1[new_fea]),sort_target1) ridge_ans = ridge.predict(mm.transform(sort_data2[new_fea])) print(‘ridge:‘,mse(ridge_ans,sort_target2)) svr = SVR(kernel=‘rbf‘,C=100,epsilon=0.1).fit(mm.fit_transform(sort_data1[new_fea]),sort_target1) svr_ans = svr.predict(mm.transform(sort_data2[new_fea])) print(‘svr:‘,mse(svr_ans,sort_target2)) estimator_RF = RandomForestRegressor().fit(mm.fit_transform(sort_data1[new_fea]),sort_target1) predict_RF = estimator_RF.predict(mm.transform(sort_data2[new_fea])) print(‘RF:‘,mse(predict_RF,sort_target2)) bst = xgb.XGBRegressor(learning_rate=0.1, n_estimators=550, max_depth=4, min_child_weight=5, seed=0,subsample=0.7, colsample_bytree=0.7, gamma=0.1, reg_alpha=1, reg_lambda=1) bst.fit(mm.fit_transform(sort_data1[new_fea]),sort_target1) bst_ans = bst.predict(mm.transform(sort_data2[new_fea])) print(‘bst:‘,mse(bst_ans,sort_target2))
结果
lr: 7.736200563088036 ridge: 3.264150764935616 svr: 3.505799850945091 RF: 0.24087179220636037 bst: 0.9945862722591914
上面的这段代码测试的是最大最小归一化情况下的结果,测试其他标准化时只需要改动mm = MinMaxScaler(),这段代码即可。
经过多次测试,统计结果如下
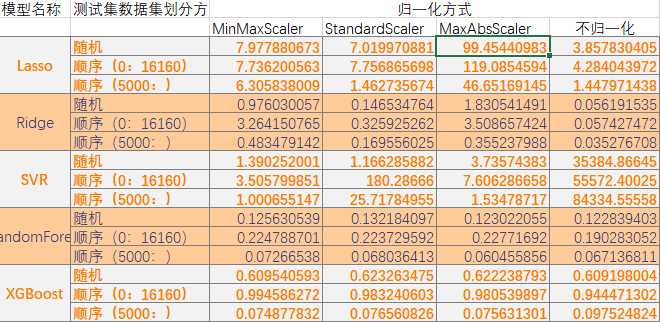
通过对比,可以发现,
标签:pearson rds target ati 机器 数据挖掘 bsp 缺陷 需要
原文地址:https://www.cnblogs.com/csu-lmw/p/9964855.html