LeetCode-二叉树的最大深度
Table of Contents
1 Easy-二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
1.1 示例:
给定二叉树 [3,9,20,null,null,15,7],
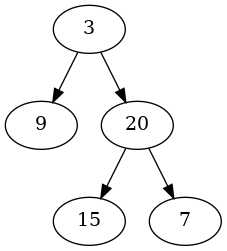
返回它的最大深度 3 。
2 自己的解答
2.1 反思
- 这题想了几种方法,还是不行,最后还是看了答案,才第一次理解了深度优先算法
3 官方解答
3.1 方法一:递归
3.1.1 算法
- 直观的方法是通过递归来解决问题。在这里,我们演示了 DFS(深度优先搜索)策略的示例。
3.1.2 代码
class Solution { public int maxDepth(TreeNode root) { if (root == null) { return 0; } else { int left_height = maxDepth(root.left); int right_height = maxDepth(root.right); return java.lang.Math.max(left_height, right_height) + 1; } } }
3.1.3 复杂度分析
- 时间复杂度:我们每个结点只访问一次,因此时间复杂度为 \(O(N)\) , 其中
N是结点的数量。 - 空间复杂度:在最糟糕的情况下,树是完全不平衡的,例如每个结点只剩下左子结点,递归将会被调用
N次(树的高度),因此保持调用栈的存储将是 \(O(N)\) 。但在最好的情况下(树是完全平衡的),树的高度将是 \(log(N)\) 。因此,在这种情况下的空间复杂度将是 \(O(log(N))\) 。
3.2 方法二:迭代
- 我们还可以在栈的帮助下将上面的递归转换为迭代。
- 我们的想法是使用 DFS 策略访问每个结点,同时在每次访问时更新最大深度。
- 所以我们从包含根结点且相应深度为 1 的栈开始。然后我们继续迭代:将当前结点弹出栈并推入子结点。每一步都会更新深度。
3.2.1 代码
import javafx.util.Pair; import java.lang.Math; class Solution { public int maxDepth(TreeNode root) { Queue<Pair<TreeNode, Integer>> stack = new LinkedList<>(); if (root != null) { stack.add(new Pair(root, 1)); } int depth = 0; while (!stack.isEmpty()) { Pair<TreeNode, Integer> current = stack.poll(); root = current.getKey(); int current_depth = current.getValue(); if (root != null) { depth = Math.max(depth, current_depth); stack.add(new Pair(root.left, current_depth + 1)); stack.add(new Pair(root.right, current_depth + 1)); } } return depth; } };
3.2.2 复杂度分析
- 时间复杂度: \(O(N)\).
- 空间复杂度: \(O(N)\).
