标签:ems 抽取 哪些 har ytd 步骤 stat out fail
目录
统计分布
抽样
置信区间
标准误
StatQuest(https://statquest.org/)是一个非常好的生物统计学课程,课程简单明了,几乎涵盖了目前生信所用到的全部统计学知识,作者不会过于使用复杂难明的式子,清晰简单的解释出复杂的统计学术语,非常适合统计学新手由浅入深地了解生信工具的内在统计学原理。
But I wanted them to understand that what I do isn’t magic – it’s actually quite simple. It only seems hard because it’s all wrapped up in confusing terminology and typically communicated using equations.
—— Josh Starmer (author of StatQuest)
本周开始,我将和大家一起学习分享StatQuest课程。
作者的所有课程都上传在YouTube上,有上网条件的可以去学习,课程列表在https://statquest.org/video-index/,整个课程体系是比较完备的,不过我会从中挑选部分内容来进行学习分享。
首先从一个场景开始,假设你在参加一个Party,无意中听到有人在讨论统计学,并且正好讨论到了统计分布,那么什么是统计分布呢?(作者举的这个话题引入的例子看起来真的很直接,这是得多喜欢统计学,连party都不放过)
假设我们在统计测量Party上参会人的身高,身高分别是5.2,5.8,5.6,5.9,5.1,6.3,...(英尺),那么你可以将他们逐个表示到一个图形上,如下图,每个红球代表一个身高数据,下面的蓝框代表身高的范围。
这样的长条组合在一起时可以叫做直方图,可以看到大部分人的身高在5-6英尺。
如果将蓝框的范围减小,那么可以看到这个直方图会变得更加平滑和精确,大部分人的身高集中在5.25-5.75之间。
如果继续增加身高数据和降低蓝框的范围,那么就可以得到下面的直方图:
同时,我们还可以在这个直方图上画一条平滑曲线,来代表这种数据趋势(大部分人的身高在5-6之间,少部分在5以下和6以上)。
这个平滑曲线还有很多优点,直方图右侧是有一个空缺的,导致无法知道身高在此区间的概率是多少,但是平滑曲线是可以给出这个答案的,而且它不会受到直方图的分段大小(图一中的蓝框)的影响。
再比如在我们没有足够的财力和精力去测定全部总体数据时,一个基于平均数和标准差的平滑曲线就可以帮我们很好的理解数据趋势。
图中的直方图和平滑曲线就是统计分布,它可以告诉我们测量值的概率是怎么分布的,主要集中在哪些范围,哪些数据出现的概率很低。
除了这个例子中的分布外,还有很多其他分布,他们的数据趋势都可以帮我们理解大量的自然数据。
绝大部分情况下,从一个特定的分布中抽样,其实就是我们利用计算机生成一个随机数,且这个随机数得抽取满足直方图或平滑曲线描述的数据趋势,以上图的趋势图为例,越靠近中间的数值越容易被抽到,而越偏离中间的数值越不容易被抽到。
进一步的,我们将可以抽样得到的样本进行t检验,就可以探索这其中发生了什么:
假设下图的一个分布,随机取了两个样本,每个样本3个数值,由于两个样本服从同一分布,因此它们都更倾向于取值在中间区域(如图),因此t检验也会给出较大的p值(p值就是可能性,p越大代表可能性越大,此处就代表两者来自于同一分布的可能性越大):
但是如果两个样本来自于两个不同的分布,那么由于它们两个的中间区域不一样,因此t检验就会倾向于给出较小的p值:
想直观了解置信区间是什么,要先从bootstrap谈起:
假定我们要估计一群雌性小鼠的体重,抽样12个小鼠,称重,计算均值如下图。
然后我们就可以使用bootstrap方法,得出这个样本的均值的置信区间,如下图,
从这12个样本数据中随机抽取12个数据(有放回);
计算这个样本的均值;
重复步骤1、2,直到计算到足够多的均值(如1000次,10000次等)
一般常用的95%置信区间就是覆盖了中间95%的均值的区间(如下图黑线所示),这其实就是置信区间了。
置信区间有什么用?
95%置信区间代表覆盖了均值95%的范围,超出这个范围的数值的出现次数都是<5%的,因此所有超出95%置信区间的数值的p值都是<0.05,都是显著的。
假如要比较雌性和雄性小鼠的体重,得到如下的置信区间结果,那么根据两者置信区间没有交界,就可以知道两者差异显著。
Bootstrap跟传统的区间估计是有些相似的,但是更有普适性。
无论总体的分布是什么样,我们知道样本均值是渐进正态分布的(假设总体均值存在)。利用渐进分布我们就可以构造样本均值的置信区间,但是问题是,要多少样本量才收敛到渐进分布呢?
如果总体不是常见分布,我们很难判断近似程度。并且,有的时候渐进分布很难写出来。Bootstrap就提供了一种灵活的,绝大多数情况都有效的方法,去判断统计量的是否合适。
误差线作为数据波动和可信度的衡量,是必须的科研绘图元素。
常见的误差数据有3种:标准差、标准误以及置信区间。
标准差:Standard Deviations,又叫做标准偏差,大部分情况下图表中使用的都是标准差;
标准误:Standard Errors,标准误差,它代表样本均值的分布情况;
置信区间:Confidence Intervals,和标准误是相关的。
标准差大家都知道,置信区间上面也说过了,那么什么是标准误呢?
如下图,假设从一个正态总体中抽样,共得到3个样本,每个样本5个数据,分别用红、绿、蓝色小球表示。
每个样本都有一个均值和标准差, 如下图下半部分所示。而对3个平均值继续求标准差,这个标准差就是均值的标准误了。当然,如果需要的话,也可以求出标准差的标准误(下图3个标准差数据的标准差)、中位数的标准误等等。
标准误可以给出抽样均值的波动程度如何,而不像标准差只是单次抽样数据的波动,因此它往往更能估计总体均值。
那么如何计算标准误呢?
少数情况下,标准误可以使用特定的公式计算。而任何情况下,你都可以使用bootstrap方法计算标准误。
此处的bootstrap方法同上面置信区间中的方法相同:
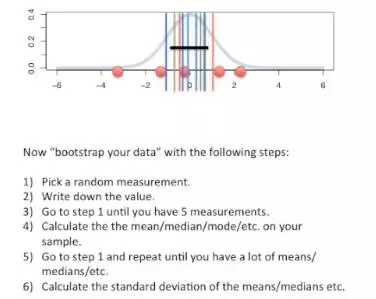
如下图,首先得到一个抽样样本,5个红色小球;
随机抽取一个测量值(红色小球),并记录;
重复随机抽取,直到拥有5个测量值(小球是有放回地抽取的);
计算均值(或其他统计量,一般情况下我们更关心均值);
重复上述4步,直到获得足够的均值数,如1000个;
计算这个1000个数值的标准差即是标准误。
标签:ems 抽取 哪些 har ytd 步骤 stat out fail
原文地址:https://www.cnblogs.com/wangprince2017/p/9973114.html