标签:des style blog http io 使用 ar 数据 sp

相传在中国宋朝时候,有一位能工巧匠叫怀丙和尚。怀丙和尚足智多谋,留下了许多有名的故事。有一年陕西发大水,冲走了一座浮桥边的两只铁牛。这铁牛重达几万斤,难以打捞。怀丙和尚命人打造了两艘大船,装满沙石,然后连接到铁牛上,然后再把船中沙石丢弃,随着船身上浮,铁牛就被捞起来了。

无独有偶,在距宋代一千多年前的西方,也有一位能人用浮力解决过难题。这个人就是希腊人阿基米德(Archimedes)。公元前260年左右,叙拉古(今意大利西西里岛)国王给阿基米德出了一个难题。原来,国王请人用黄金打造了一顶纯金王冠,但是国王怀疑王冠掺假,于是请阿基米德来甄别。阿基米德把王冠放到天平的一端,然后再把等重的金块放上天平的另一端,最后把天平浸入水中。结果天平入水之后不再保持平衡,王冠掺了假。
这两个故事都是利用了浮力来化解难题,但是有一个非常不一样的地方。捞铁牛的古人运用经验来定性解决问题,并没有进行系统研究和归纳。而阿基米德从数学入手,定量分析,归纳出了“阿基米德原理”。
“阿基米德原理”提出:流体中的物体受到向上的浮力,其浮力大小等于其排开流体的重量。其中“流体”可为液体或气体。“重量”是因为万有引力而引发的作用力。这是最早的流体力学相关的能够定量计算的定律。

十五世纪文艺复兴期间,艺术大师达芬奇(da Vinci)继续对流体的特点进行了研究。他仔细思考了鸟类的飞翔提点,观察了水面波纹传播的规律,把兴趣的重点放在“涡漩(Eddy)”上。常态下的流体是稳定的,但是当流体的速度达到一定大小的时候,稳定性就会被破坏,形成“湍流”。“湍流”就是由一个个涡漩组成的。
达芬奇更加有趣的分析是关于液体的体积流量守恒原理:在同一管道中,相等的时间里流过的不同面积的横截面的流体体积是相同的。这个结论看似简单,其实暗含一个极其重要的假设:流体不可压缩。

1589年左右,意大利科学家伽利略(Galileo)完成了世界上第一本完整的物理学教科书:《流体力学》。这本教科书很有特点,伽利略使用了讽刺喜剧般讲故事的方法来阐述他的观念,令读者感到大为好奇,产生了一定影响。
1641年,意大利科学家托里拆利(Torricelli)设计了一个著名的实验来测定气体压力。他发现封闭真空水银管中的水银高度一直是76厘米,因为空气有重量,大气压力把水银压在了76厘米处。
托里拆利深受伽利略影响。早在1628年,托里拆利的导师卡斯德利就写了一本关于流体力学的著作,托里拆利当即指出其中的一处重要错误。卡斯德利正是伽利略的学生。卡斯德利认为,如果在一个水箱侧面钻一个孔,那么小孔处水流速度与小孔距离水面的距离成正比。托里拆利的实验表明,应该是与距离的平方根成正比。托里拆利的学说产生了深远的影响,导致流体力学从力学中分离出来,成为了独立的一个学科。有趣的是,伽利略和托里拆利的结论让很多阿基米德的理论破产。
法国数学家帕斯卡(Pascal)承袭了托里拆利的工作。帕斯卡在实验后认为:密闭容器中流体任意一部分的压强向流体的各个方向传递,而且大小相等。帕斯卡定律的数学描述为:F1/A1 = F2/A2。F1,F2是施加在流体上面的力,A1,A2是施加力的作用面积。帕斯卡定律在液压传动方面有非常重要的意义。“帕斯卡”也变成了国际压强单位。
与此同时,爱尔兰科学家波义耳(Boyle)着手研究空气的“弹性”。他找来一只羊的膀胱,用抽气机抽出气体,结果膀胱变小。充入气体,膀胱又变大。1662年,波义耳仔细研究了实验数据,提出了“波义耳定律”:气体的压强与体积的乘积是一个常数。

1687年,牛顿出版了《自然哲学的数学原理》。牛顿等人认为古老的流体力学与工程实际相差甚远,决定增加一些系数。牛顿把物体间的摩擦力引入流体中,认为流体内也存在与摩擦力类似的“粘性力”。法国物理学家达朗贝尔(Rond d‘Alembert)按照牛顿的思路用水中的船只作了实验,证明了流体中的粘性阻力与物体运动速度成平方关系。
1755年,瑞士科学家欧拉(Euler)假设了一种理想流体(没有粘性,不可压缩)并列出了流体力学的基本方程。在这个模型中,决定流体运动的只有压力。模型定义的三个向量场分别为速度场u,压力场p,和密度场rho,它们都是位置s和时间t的函数。
这个等式看似复杂,其实就是牛顿第二定律的翻版。牛顿第二定律说“物体的加速度与物体所受的合外力成正比,与物体质量成反比”。数学表达式为a = F / m。欧拉公式也非常类似,左边两项合起来是质点运动的加速度,右边表示单位质量的微粒压力变化的总合。
左边第一项表示空间s中的质点速度的时间变化率。左边第二项表示速度为u的质点经微小时间变化后到达了另一个位置,新的位置和原来的位置的速度不一样。u对s的偏导数即为速度在不同位置的变化率,乘上u就得到了新的位置速度改变量。我们在中学物理里面只学了第一项,是因为对于固体(solid)和粒子我们有不同的定义。第二项是关于流体粒子运动带来的变化。
如果考虑三维情况,令坐标轴为u,v,w,并考虑重力方向,可以推导以下欧拉方程组。
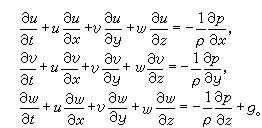
欧拉方程表明,由液体的内部压力可以模拟液体微粒的运动方式,反过来由速度也可以解出内部压力。欧拉方程是非线性方程,即使用今天的电子计算机来求解也很困难。在两百多年前的欧洲,人们试图化简这个方程,其中以“伯努利方程”最为著名。
瑞士学者D.伯努利(Bernoulli)认为,对于密度不变,定常流动(流场不随时间变化,流场只是空间坐标的函数)的流体的一维情景,可以概括如下:
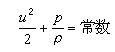
伯努利方程可由欧拉方程做出如上化简后积分得到。从我们学过的动能定理知道,速度的二次方其实是物体的动能。所以伯努利方程实际告诉了我们是压力导致了动能的变化。由于没有考虑粘性,其实右边的“常数”其实并不准确。
十八世纪的法国科学家拉格朗日(Lagrange)提出了研究流体力学的一种方法,它着眼于单个质点的运动,分析其运动轨迹,从而得出整个流体的运动。由此引出的“半拉格朗日”法仅研究终点在空间节点上的质点。相比较而言,欧拉的方法着眼于空间点,把空间分成一个网格体。网格上的每个节点上有速度、质量和密度等量,这些量的变化规律反映了流体的变化规律。拉格朗日又称“质点法”,欧拉法又称“空间法”。
就像前面说过的,尽管欧拉、伯努利运用了牛顿开创的力学定律和微积分,但是没有考虑牛顿提出的流体粘性,理论结果与实验结果相去甚远。而过于精细的方程又无法求解。流体力学分化为了两派:支持继续进行纯理论推导的流体理论派,支持采用半理论半实际测量的水力派。两派相互争辩,这样又过了一百多年。
纯理论研究想要获得突破,关键是要建立合适的粘性模型。1822年,纳维最早使用了微分方法建立了不可压缩粘性流体的方程组。1845年,英国人斯托克斯进一步完善了这些方程,引入粘性系数。这些方程通常被称为“Navier-Stokes equations”(NS方程组)。
NS方程组告诉了我们一种液体究竟有多粘。它有几个基本假设:1、流体必须是连续的(内部没有空隙,比如溶解的气泡);2、所有的向量场(速度、压强、密度…)全部可微分。NS方程组的求解极其困难,工程中的大多数问题只能获得近似答案。目前科学家只求解得到了70多个精确的特解。
NS方程极其复杂。假如我们讨论不可压缩流体,并且假设粘性系数是常数,可以把NS方程组化简为以下的简单形式:
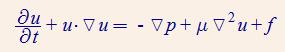 (1)
(1)
![]() (2)
(2)
(1) 式左侧就是欧拉方程的加速度。右侧第一项是欧拉方程的压力因素。右侧第三项f是液体所受合外力。右侧第二项就是斯托克斯引入的粘性项。换句话说,欧拉方程就是不可压缩流体粘性系数为0的特殊情况。如果仔细观察第二项的话,会发现它与热运动的扩散方式非常相似。
(2) 式表现了流体的不可压缩性,是动量守恒方程。
尽管NS方程组也只是一个近似的描述,但仍然使理论流体力学向前跨进了一大步,可谓进入了流体力学史上第一个巅峰时刻。NS方程组是对于过去流体力学历史的总结,也是未来流体发展的惊人预言,近现代理论流体力学的研究纷纷以NS方程组为原始出发点。

还记得令达芬奇着迷的“湍流”吗?NS方程只对稳定流体有效,无法解决“湍流”问题。人们把NS方程能解决的流体问题归纳为光滑流动的“层流”问题,与“湍流”相对应。1883年,雷诺(Reynolds)仔细研究了层流和湍流的运动机制,用非压缩NS方程推导了一个数字,并用这个数字来判定流体到底是层流还是湍流。雷诺数是惯性力(不受外力就做匀速直线运动)和粘性力(流体摩擦力)的比值。当雷诺数比较小时,粘性力大于惯性力,流速的扰动会迅速衰竭,流体运动稳定,是层流;反之,惯性力大于粘性力,微小的扰动会迅速发展成为巨大的扰动,形成不规则的湍流。但是直到今天,湍流仍然难以刻画,湍流的真正形成机制仍然是一个谜团。
1904年,德国物理学家普朗特(Prandtl)提出了“边界层理论”。雷诺数很大的时候,流体内部应该为湍流,但是普朗特认为在接近流体边缘的时候仍然是层流。通过引入“边界层”,可以更好地化简NS方程组。普朗特的另一大贡献是把流体理论派和水力派统一了起来,“边界层理论”就是理论与实践结合的产物。

20世纪初,人们开始研究飞机所需要的空气动力学,普朗特开创了以流体力学为基础的机翼理论,告诉了人们为什么空气可以把如此沉重的飞机送上天空。1911年,匈牙利人冯卡门(von Kármán)成为普朗特的学生,他提出了“卡门涡街”的理论。在流体中设置阻流体,在阻流体下游会产生交错的涡旋,就好像街道两边的街灯一样。
冯卡门在加州理工学院成立了喷气推进实验室,钱学森成为了他的学生。他们共同研究了亚声速流动中压缩性对流体表面压力影响的公式,叫“卡门-钱学森公式”。冯卡门在回忆录《钱学森与红色中国》中评价道:“美国火箭领域中最伟大的天才之一,我的杰出门生”。
1955年,受美国麦卡锡主义的迫害,钱学森回到中国。华裔作家张纯如在《钱学森传》中评价道:“世人对钱学森的印象并非基于他在美国的研究成果,而是由于他遭驱逐后在中国领导科学的成就。他绝对是位杰出的一流科学家,但跟他共事过的人都一再向我强调,他还不够资格跟牛顿或爱因斯坦相提并论,甚至也不及他在加州理工的导师冯卡门。尽管他在理论方面下的功夫,对美国气体动力学的发展极具价值,但他既不曾带动革命,也未能创造新领域。如果他一九五五年就去世,不曾回到中国,他的一生就不可能成为一流传记的素材。”

1961年,美国气象学家洛伦茨(Lorenz)在模拟大气运动的时候为了省事,将本来是6位小数的输入数据截成了3位小数。他发现,0.0001的输入误差能够导致完全相反的结果。洛伦茨建立了新的气候数学模型,这个模型可以得出无穷多个发散的结果。他总结道:天气不停地变动根本就是无法正确预测的。1979年,洛仑兹发表了“蝴蝶效应”演说,认为巴西的蝴蝶振一振翅膀,可以导致德州的一场龙卷风。这就是著名的“混沌理论”。
流体力学的发展自阿基米德开始,历经了上千年的研究。有人说,混沌理论的起始,就是经典科学的结束,但是流体力学还远远没有到完结的时候。即使现代人能够运用计算机来进行复杂的运算,模拟湍流和混沌仍然是不可能的任务。
2000年,美国克雷数学研究院公布了七道历史性的“千禧年难题”,承诺给能够解答任何一题的人一百万美元。其中第六道就是NS方程组的存在性和平滑性证明,目前仍无人认领此奖。即使是相对简单的欧拉方程,目前也无法证明其一定存在解。
翱翔的飞鸟,起伏的波涛,汹涌的火焰,皑皑的冰雪,人类试图寻找隐藏在背后的终极答案。相信有一天,大自然的杰作将以本来面目呈现在我们面前。
标签:des style blog http io 使用 ar 数据 sp
原文地址:http://www.cnblogs.com/liangliangdetianxia/p/4020829.html