标签:time pre turn .com ati integer from 重复 can
53. Maximum Subarray
Given an integer array
nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.Example:
Input: [-2,1,-3,4,-1,2,1,-5,4], Output: 6 Explanation: [4,-1,2,1] has the largest sum = 6.
思路:当前的最大值怎没递归呢?就是取(前一个最大的值)和(前一个值加上当前值)的最大者
dp[i]=max(dp[i-1]+当前值nums[i] , 之前的最大值max)
class Solution { int maxSubArray(vector<int> &nums) { int n =nums.size(); vector<int> dp(n,0);//dp[i] means the maximum subarray ending with nums[i]; dp[0] = nums[0]; int max = dp[0]; for(int i = 1; i < n; i++){ dp[i] = nums[i] + (dp[i - 1] > 0 ? dp[i - 1] : 0); //前面的dp[i-1]小于0则清空重新从0开始计数 max = max(max, dp[i]); //当前的dp[i]和之前的最大的某个dp比较,取最大 } return max; } };
64. Minimum Path Sum
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
Example:
Input: [ [1,3,1], [1,5,1], [4,2,1] ] Output: 7 Explanation: Because the path 1→3→1→1→1 minimizes the sum.
思路:递归策略:当前的格子等于前一列格子加上一个格子。最左边只能加上一个格子,最上边的只能加做一个格子。
///不优化 class Solution { public: int minPathSum(vector<vector<int>>& grid) { int m = grid.size(); int n = grid[0].size(); vector<vector<int> > sum(m, vector<int>(n, grid[0][0])); for (int i = 1; i < m; i++) //左格子 sum[i][0] = sum[i - 1][0] + grid[i][0]; for (int j = 1; j < n; j++) //右格子 sum[0][j] = sum[0][j - 1] + grid[0][j]; for (int i = 1; i < m; i++) //既不是左格子也不是右格子,而是中间的格子 for (int j = 1; j < n; j++) sum[i][j] = min(sum[i - 1][j], sum[i][j - 1]) + grid[i][j]; return sum[m - 1][n - 1]; //返回最右下角的格子值 } }; ////两个一位数组的优化
//思路:当前的格子只和前一个格子和上一个格子有关,所以可以使用两个数组来保存。一个数组pre用来保存前一列的递归值,一个数组cur保存当前列的递归值
class Solution { public: int minPathSum(vector<vector<int>>& grid) { int m = grid.size(); int n = grid[0].size(); vector<int> pre(m, grid[0][0]); vector<int> cur(m, 0); for (int i = 1; i < m; i++) pre[i] = pre[i - 1] + grid[i][0]; for (int j = 1; j < n; j++) { cur[0] = pre[0] + grid[0][j]; for (int i = 1; i < m; i++) cur[i] = min(cur[i - 1], pre[i]) + grid[i][j]; swap(pre, cur); } return pre[m - 1]; } }; ///一个一维数组的优化
//从第二种方法知到,保留的pre数组其实也就是cur数组的前一次,所以可以直接使用一个数组cur就够了
class Solution { public: int minPathSum(vector<vector<int>>& grid) { int m = grid.size(); int n = grid[0].size(); vector<int> cur(m, grid[0][0]); for (int i = 1; i < m; i++) cur[i] = cur[i - 1] + grid[i][0]; for (int j = 1; j < n; j++) { cur[0] += grid[0][j]; for (int i = 1; i < m; i++) cur[i] = min(cur[i - 1], cur[i]) + grid[i][j]; } return cur[m - 1]; } };
第二种方法图解:
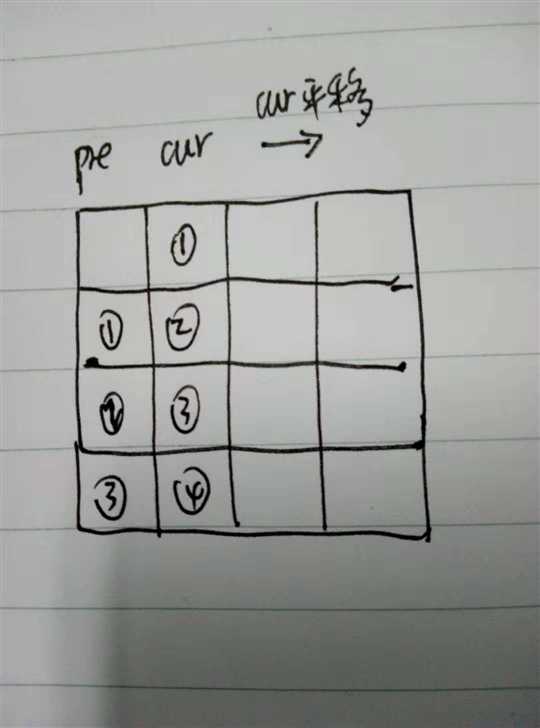
pre代表当前格子的前一个格子,cur代表当前格子+上一个格子+前一个格子,迭代完当前列后,后面的列重复前面的动作。
标签:time pre turn .com ati integer from 重复 can
原文地址:https://www.cnblogs.com/hotsnow/p/9974813.html