标签：ISE   lis   连接   pen   很多   adt   深度优先遍历   个数   node   

学号 20172326 《程序设计与数据结构》第九周学习总结

教材学习内容总结

• 图：图（Graph）是一种复杂的非线性结构，在图结构中，每个元素都可以有零个或多个前驱，也可以有零个或多个后继，也就是说，元素之间的关系是任意的。与树的区别在于树中的一个结点只有一个前驱，也就是说只有一个父结点。但图中的顶点（结点）是没有这种限制关系的。
• 无向图：边为无需结点对的图。也就是说，现有两个顶点A、B.(A,B)与（B，A）效果相同。当两个顶点之间有边连接，也就是说这两个顶点是邻接的，也称作邻居。一个顶点用一个边连接自己被称为环，例如（A,A）。完全图是指无向图有最大数目的联通顶点，换句话说，每个顶点之间都有一条边连接。根据等差数列求和公式可以求出一个完全图的边数（一般来说，不考虑自循环的情况）。路径是指一个顶点到另外一个顶点所需要的最少边数，或是所途径的顶点数-1。连通，每个顶点之间都可以通过边到达彼此，不一定两个顶点之间必有直接连通的边，间接的也可以。环路是指从一个顶点开始，并最终以这个顶点为终点，途径某几个或者全部顶点的路径。
• 有向图：如果无向图中的边是一条双向车道，那么有向图中的边就是一条单行道，方向取决于定义。因此，看似每个定点之间都有边的有序图不一定就是一个连通图。
• 拓扑序，书上没有详细讲，出于好奇，我查了查它的原理。首先，确定顶点中的无依赖顶点，也就是没有顶点到该顶点的边的顶点。将这些顶点存入一个队列中去。并从图中将其删去。以此为规则，逐步递归，最终将他们都存入队列。
  
• 广度优先遍历法：在一定程度上，与树的层序遍历法有一定的相似性。首先，确定一个顶点开始遍历，之后是该顶点路径相同的的邻顶点。每次优先处理顶点的邻顶点。

• （图）

• 来看这张图，从9开始。以路径为1的开始遍历，那么就是6、7、8这三个顶点，紧接着，根据优先顶点的邻顶点原则，为3、4，之后为7的邻顶点-5。8没有邻顶点，跳过，尔后又是1、2。至此，广度遍历完成。在书上的实现过程中，先后使用了队列保证先进先出的性质，以及将其加入列表中。
• 深度优先遍历法：选定一个顶点，遍历其邻顶点。但是首先将一个邻顶点的全部邻顶点遍历完，再返回，进行下一个邻顶点的遍历。类似于树中的前序遍历法。
• （无序图）
• 顺序为A -> C -> B -> D -> F -> G -> E。对于相同路径的顶点来说，遍历的先后由具体的代码决定，其本质上是一致的。
• （有向图）
• 与无序图基本类似，但区别在于部分边可能是有向的，所以要对不能到达的顶点进行判断。该图的遍历顺序为A -> B -> C -> E -> D -> F -> G
• 连通性：只要所有的顶点之间是连通的，那么所有的顶点元素在遍历一遍后都可以得到存储。但是如果有未连通的顶点，顶点元素与存储元素之间势必不等。通过此来判断是连通。
• 最小生成树：将一个加权图变为一棵树，当然，树也是图的一种。最小生成树的特点在于将其边的权重总和小于等于同一个图任何生成树的权重总和。有两种算法可以用来实现最小生成树
• 普里姆算法（Prim算法）：首先输入一个顶点。根据权重大小来选择小权的边。不断进行循环，直到将每个顶点连通。注意，顶点之间边的权重比较并不是随着连接新的顶点就只单独地看该顶点的邻顶点。始终以整体来看。哪个顶点与其邻顶点的边的权小就选择那条边。

• （图）
  

• Kruskal（克鲁斯卡尔）算法：与普利姆算法不同。首先寻找寻找一条权最小边，然后是第二条、第三条。在此过程中，可以使边与边之间连起来，并且最终都要连接起来。但是，不能出现回路。例如，目前有一条边是当前未连接最小的边。但如果连接这条边。这会使得最小生成树出现回路。那么将不被允许，此时就要放弃这条边。
• 邻接列表：用链表来存储每个结点之间的边。对于无向图，因为边存在于两个顶点之间。所以会存在两个结点均存储了相同边。

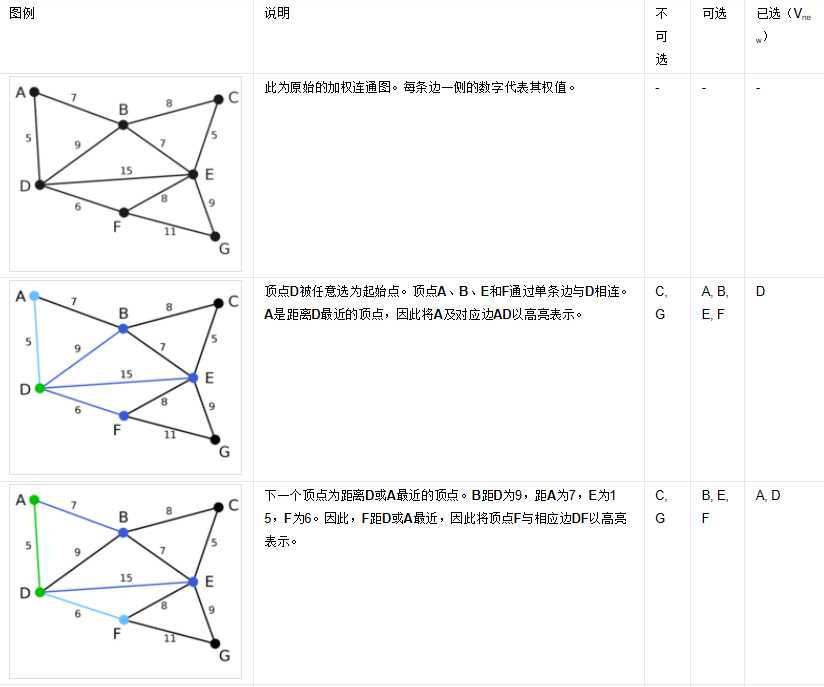
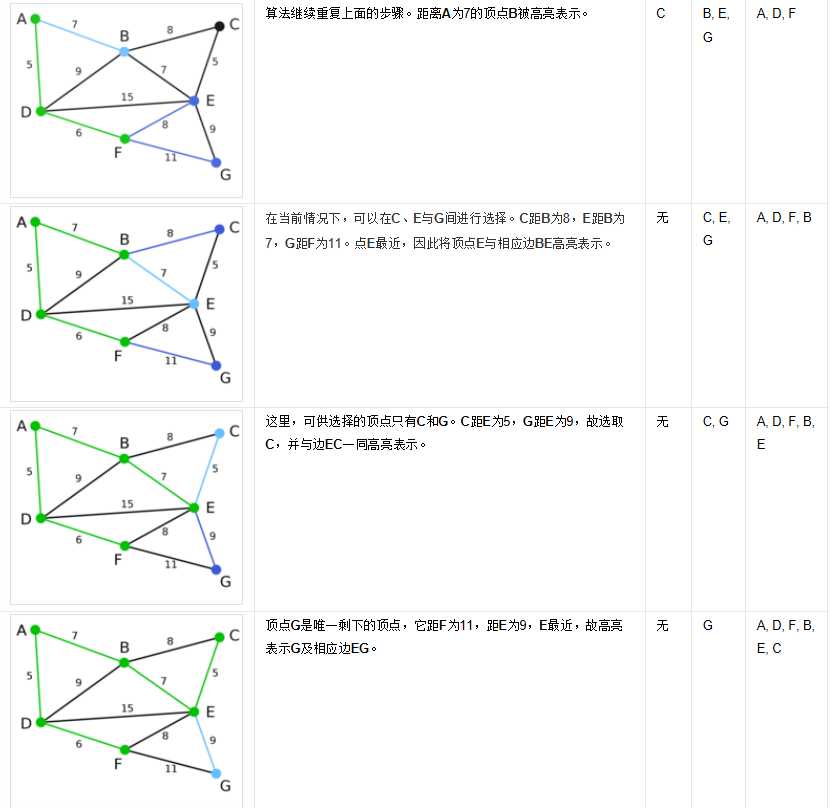
• 邻接矩阵：使用布尔数组来实现存储边。将存在边的位置记录为true，无位置的记录为false。对于一个无向图，其存储结果是一个对称矩阵。但是对于有向图来说，因为边的单向性，结果将不同。

  教材学习中的问题和解决过程

• 问题1：广度遍历法与深度遍历法通过什么实现了其各自特点要求的遍历？

• 问题1理解：首先打眼一看，似乎两个方法没什么区别。BFS相当于是从第一个顶点开始遍历完其所有的邻顶点的邻顶点再进行下一个的遍历。DFS类似于前序遍历。 通过对课本代码的分析。找出了几个关键部分代码。第一点，使用了不同的数据结构对其进行存储。BFS使用了队列的方式。DFS使用了栈进行存储。下面就详细的进行分析。先看BFS的代码。

while (!traversalQueue.isEmpty())
        {
            x = traversalQueue.dequeue();
            resultList.addToRear(vertices[x.intValue()]);

            //Find all vertices adjacent to x that have not been visited
            //     and queue them up 
            
            for (int i = 0; i < numVertices; i++)
            {
                if (adjMatrix[x.intValue()][i] && !visited[i])
                {
                    traversalQueue.enqueue(new Integer(i));
                    visited[i] = true;
                }
            }
        }

首先，先声明，书上的方法均是是基于邻接矩阵实现的。具体来讲也就是两个布尔数组来确定顶点与顶底之间是否有边。将顶点进入队列后，再取出放入列表之中。然后根据邻接矩阵来判断边，也就是找出所有的邻接顶点。依次存入队列之中。当找到所有的邻接顶点后。将第一个进入队列的顶底取出，找出其所有的邻接顶点。之后再进行下一个顶点的邻接顶点的查询。通过队列先进先出的顺序，将所有顶点按照类似于树的先序遍历的方法储存起来。那么，如何防止出现重复的结点呢？建立的boolean型的visited数组就可以解决这个问题，初始化时所有结点都是false也就是未被访问。当访问到一个顶点后，将其标记为true。当下一次再访问到这个顶点后。就进行跳过。

• DFS代码，

while (!traversalStack.isEmpty())
        {
            x = traversalStack.peek();
            found = false;

            //Find a vertex adjacent to x that has not been visited
            //     and push it on the stack 
            for (int i = 0; (i < numVertices) && !found; i++)
            {
                if (adjMatrix[x.intValue()][i] && !visited[i])
                {
                    traversalStack.push(new Integer(i));
                    resultList.addToRear(vertices[i]);
                    visited[i] = true;
                    found = true;
                }
            }
            if (!found && !traversalStack.isEmpty())
                traversalStack.pop();
        }

众所周知，栈是后进先出的。那么，如果以顶点V开始，它的第一个邻顶点为U。那么它入栈，紧接着寻找U的第一个邻顶点，然后将其入栈。每次使用peek方法获取当前栈顶元素，也就是上一个顶点的第一个邻顶点。当找不到时，将其弹出。就好比一棵树，当把这一棵子树的所有结点找完后，就去下一棵子树找。同理，循环会将已经都访问过的顶点弹出栈，直到找到没有访问过邻顶点的顶点。按照这个顺序，将顶点按照深度优先的顺序存入列表中。

• 问题2：最短路径的实现问题
• 问题2理解：实现最短路径，这里主要指的是无向图。首先，我们分别使用两个数组，一个用于存放不同的索引的深度，一个存放前驱结点。

int[] pathLength = new int[numVertices];
int[] predecessor = new int[numVertices];

之后根据放入的顺序进行遍历，如果与顶点有边，那么，将其存入，之后用队列，将其存储。如果只是需要具体的数字，我们直接将其对应的索引对应的数字返回即可。

while (!traversalQueue.isEmpty() && (index != targetIndex))
        {
            index = (traversalQueue.dequeue()).intValue();

            //Update the pathLength for each unvisited vertex adjacent 
            //     to the vertex at the current index. 
            for (int i = 0; i < numVertices; i++)
            {
                if (adjMatrix[index][i] && !visited[i])//
                {
                    pathLength[i] = pathLength[index] + 1;
                    predecessor[i] = index;
                    traversalQueue.enqueue(new Integer(i));
                    visited[i] = true;
                }
            }
        }

但是，我们不妨再将其顺序返回，使得其更加直观。通过之前对部分方法的分析我们不难发现，对于这种非线性数据结构，有时使用队列来达到层序遍历，而使用栈达到前序遍历（后序遍历）这时，我们就用栈（后进先出）来实现。

StackADT<Integer> stack = new LinkedStack<Integer>();
        index = targetIndex;
        stack.push(new Integer(index));
        do
        {
            index = predecessor[index];
            stack.push(new Integer(index));
        } while (index != startIndex);
        
        while (!stack.isEmpty())
            resultList.addToRear(((Integer)stack.pop()));

• 同时，还出现了一种新的问题，也就是，从代码当中，我们无法找到体现比较的过程。但是依旧可以实现返回最短路径的深度。原因何在？
• 其实，刚刚已经提到，使用了队列的方法，从而实现了层序遍历的方法，这样一来，避免了那些曲里拐弯的路径，所以，不需要比较，就可以实现。

代码调试中的问题和解决过程

• 问题1：实现pp15_7时如何解决权重的问题
• 问题1解决方案：之前介绍过了prim算法。同时，还有一种迪杰斯特拉算法（Dijkstra）因此，在此介绍一下。选择一个初始顶点，存入一个dist数组中，然后，挨个遍历，和顶点有边的存入其权重。自己的位置为0，没有边的位置存的是无穷大。之后，对没有直接连接的进行处理。从初顶点到其可能有多条路径，对应多种选择，对应多种不同的权重和，经过选择最小的权重。放至那个位置。
• 在熟悉了这个方法后，开始编程。首先，把所有的权重放入dist数组中，对于没有直接连接的位置，定义为无穷大，这里怎样定义无穷大呢？

public static final double POSITIVE_INFINITY = 1.0 / 0.0;

就是无穷大了，它被定义于Double中，可以直接调用。然后，首先对目前已有的“非0（不是它自己）非-1（两者之间有边）。在这个基础上，选出最小的值，存入列表之中。之后，用最小值的索引值来继续向下遍历。换句话说，对于dist数组中存取数据为无穷大的（也就是计算出未直接与初顶点相连的间接权重）

for (int i = 0; i < numVertices; i++) {
            flag[i] = false;
            dist[i] = adjMatrix[start][i];
        }

for (int j = 0; j < numVertices; j++) {
                if (flag[j] == false && dist[j] < min && dist[j] != -1 && dist[j] != 0) {
                    min = dist[j];
                    k = j;
                }
            }

这里的k就是最小权的索引值。每次都选择最小的权重边作为路径。然后重复这个过程。最终，整个disc数组的每个索引对应的就是从初顶点到该对应索引的最短权重路径。我们根据需要，取出即可。

  for (int j = 0; j < numVertices; j++) {
                if (adjMatrix[k][j] != -1&&dist[j]!= -1) {
                    double temp = (adjMatrix[k][j] == Double.POSITIVE_INFINITY
                            ? Double.POSITIVE_INFINITY : (min + adjMatrix[k][j]));
                    if (flag[j] == false && (temp < dist[j])) {
                        dist[j] = temp;
                    }
                }
            }
        }
        return dist[end];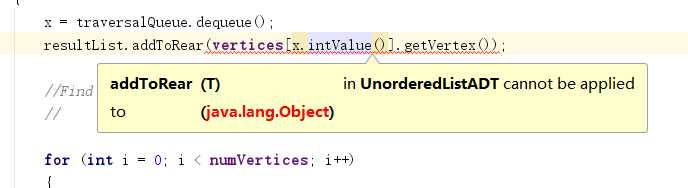

• 问题二：T和Objiect的区别
• 解决过程：，按理来说，这两者似乎没什么区别。在上学期的学习中，有一个定义让我印象深刻，就是Object类是所有类的父类。所以Object范围非常广，而T从一开始就会限定这个类型（包括它可以限定类型为Object）。
  Object由于它是所有类的父类，所以会强制类型转换，而T从一开始在编码时（在写代码时）就限定了某种具体类型，所以它不用强制类型转换。所以使用起来就更加方便。

代码托管

上周考试错题总结

• 错题1及原因，理解情况
• Though not a queue at all, a minheap provides an efficient implementation of a _____________.
• 堆是一种树，根据定义对数据进行存储，但是虽然它不是一种线性数据结构，但可以作为与其类似的定义高效率的完成类似队列 的工作。
• 错题2及原因，理解情况
• In an array implementation of a binary tree, the root of the tree is in position 0, and for each node n, n’s left child is in position ________ and n’s right child is in position ________.
• 数组实现二叉树，其左孩子永远在2n + 1处，右孩子在2(n + 1)处。
• 错题3及原因，理解情况
• The removeMin operation for both the linked and array implementations is
• 用数组或者队列实现最小堆的效率logn。
• 错题4及原因，理解情况
• Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full.

• 对于堆，插入元素时，为了满足其完全树的定义，当一层未满时，优先将元素放至左孩子位置，如左孩子填满，则放至右孩子处。如果一层满。则放在下一层的第一个位置。

  其他（感悟、思考等，可选）

• 图的情况有很多种，有向和无向，有权重和无权重，遍历方法也比较难懂，需要继续学习

  结对及互评

• 博客中值得学习的或问题：
  排版精美，对于问题研究得很细致，解答也很周全。

• 代码中值得学习的或问题：
  代码写的很规范，思路很清晰，继续加油！

点评过的同学博客和代码

• 本周结对学习情况
• 20172313

• 20172332

  结对学习内容

• 第十五章 图

学习进度条

参考资料

• https://www.cnblogs.com/skywang12345/p/3245399.html
• https://www.cnblogs.com/skywang12345/p/3603935.html
• https://www.cnblogs.com/ysocean/p/8032659.html#_label0_2

《程序设计与数据结构》第九周学习总结

标签：ISE   lis   连接   pen   很多   adt   深度优先遍历   个数   node   

原文地址：https://www.cnblogs.com/326477465-a/p/9976176.html