标签:初始 优化问题 影响 学习 初始化 smo max 高效算法 线性
数据集$D = \{ ({{\bf{x}}_1},{y_1}),({{\bf{x}}_2},{y_2}),...,({{\bf{x}}_m},{y_m})\} $,其中${{\bf{x}}_i} = \{ {x_{i1}},{x_{i2}},...,{x_{id}}\} $,包含d维特征,${y_i} \in \{ - 1, + 1\} $。
分类学习就是在样本空间里找到一个超平面,能够分离开“+”、“-”两类。如下图所示,在二维特征的样本空间里,找到一条线能够分离开两类。但是针对该数据集D,这样的线可能有很多,我们应该用哪一个呢?直观上看,应该是正中间加粗的那条线是“最合适”的线,对训练集D局部扰动的“容忍”性最好。换言之,这个划分超平面所产生的分类结果是最鲁棒的,对未见示例的泛化能力最强.
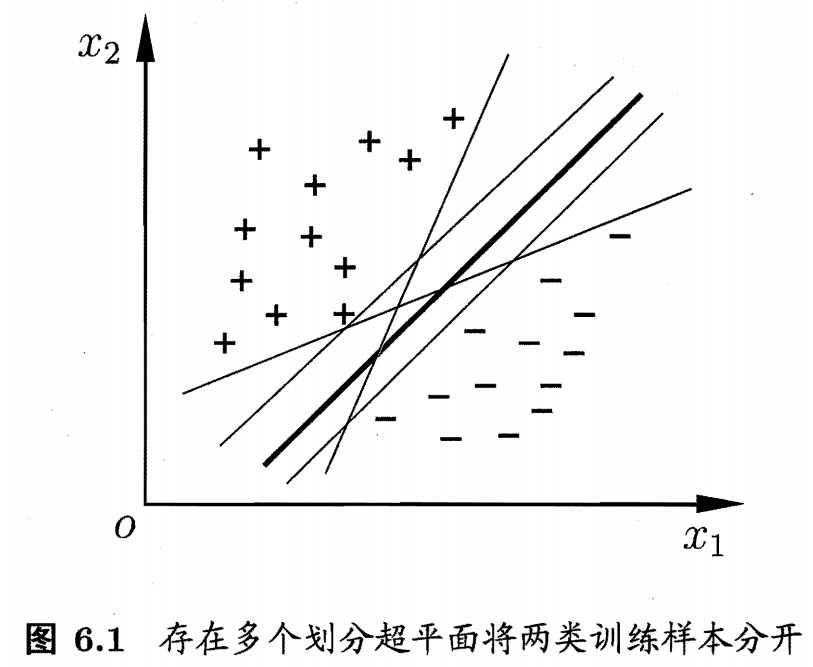
该超平面可通过线性方程来描述,${{\bf{\omega }}^T}{\bf{x}} + b = 0$,该超平面记为$({\bf{\omega }},b)$。
假设超平面$({\bf{\omega }},b)$能将训练样本正确分类,即对于$({{\bf{x}}_i},y_i) \in D$,若$y_i = +1$,则有${{{\bf{\omega }}^T}{{\bf{x}}_i} + b}>0$,若$y_i = -1$,则有${{{\bf{\omega }}^T}{{\bf{x}}_i} + b}<0$。令,
$\left\{ {\begin{array}{*{20}{c}}
{{{\bf{\omega }}^T}{{\bf{x}}_i} + b \ge + 1,{y_i} = + 1}\\
{{{\bf{\omega }}^T}{{\bf{x}}_i} + b \le - 1,{y_i} = - 1}
\end{array}} \right.$
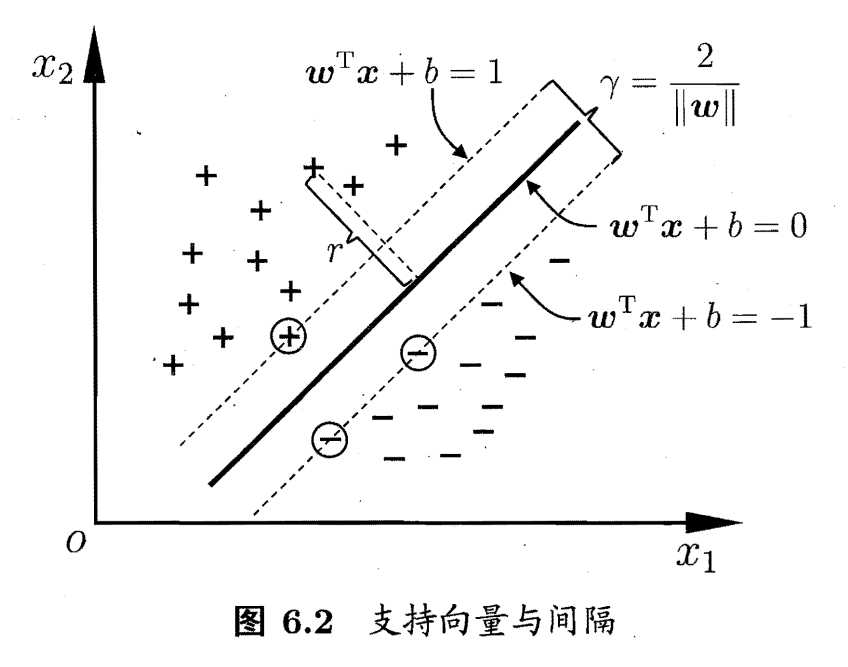
距离超平面最近的这几个训练样本点(如上图中被圈出来的三个样本点)等号成立,被称为"支持向量" (support vector),两个异类支持向量到超平面的距离之和为 $\gamma = \frac{2}{{\left\| {\bf{\omega }} \right\|}}$,称为“间隔”。
我们希望在满足样本约束${y_i}({{\bf{\omega }}^T}{{\bf{x}}_i} + b) \ge 1$的条件下,找到具有最大间隔的划分超平面$\mathop {\max }\limits_{{\bf{\omega }},b} \frac{2}{{\left\| {\bf{\omega }} \right\|}}$。
支持向量机的基本型如下,
$\begin{array}{l}
\mathop {\min }\limits_{{\bf{\omega }},b} \frac{1}{2}{\left\| {\bf{\omega }} \right\|^2}\\
{\rm{s}}{\rm{.t}}{\rm{. }}{y_i}({{\bf{\omega }}^T}{{\bf{x}}_i} + b) \ge 1,i = 1,2,...,m
\end{array}$
我们希望求解支持向量机基本型的最小化问题,来得到大间隔划分超平面所对应的{+1,-1}二分类模型
$f({\bf{x}}) = {{\bf{\omega }}^T}{\bf{x}} + b$
怎么求这个凸优化问题,求得最优模型参数$\bf{\omega }, b$呢?
我们对每条约束引入拉格朗日乘子$\alpha_i \ge 0$,则该问题的拉格朗日函数可写为,
$L({\bf{\omega }},b,{\bf{\alpha }}) = \frac{1}{2}{\left\| {\bf{\omega }} \right\|^2} + \sum\limits_{i = 1}^m {{\alpha _i}\left( {1 - {y_i}\left( {{{\bf{\omega }}^T}{{\bf{x}}_i} + b} \right)} \right)} $
该优化问题表示为,
$\mathop {{\rm{min}}}\limits_{{\rm{w,b}}} \mathop {\max }\limits_{{\alpha _i} \ge 0} L(w,b,\alpha )$
转化为对偶问题,
$\mathop {\max }\limits_{{\alpha _i} \ge 0} \mathop {{\rm{min}}}\limits_{{\rm{w,b}}} L(w,b,\alpha )$
求$L({\bf{\omega }},b,{\bf{\alpha }})$对$\bf{\omega }$和$b$的偏导为零
$\begin{array}{l}
{\bf{\omega }} = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}} {{\bf{x}}_i},\\
0 = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}} .
\end{array}$
则对偶问题表示为
$\begin{array}{l}
\mathop {\max }\limits_{\bf{\alpha }} \sum\limits_{i = 1}^m {{\alpha _i} - } \frac{1}{2}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{\alpha _i}{\alpha _j}} } {y_i}{y_j}\left\langle {{{\bf{x}}_i},{{\bf{x}}_j}} \right\rangle \\
s.t. \sum\limits_{i = 1}^m {{\alpha _i}{y_i}} = 0,\\
{\alpha _i} \ge 0,i = 1,2,...,m.
\end{array}$
解得${\bf{\alpha }}$后,求出$\bf{\omega }$和$b$即可得到模型,
$\begin{array}{l}
f({\bf{x}}) = {{\bf{\omega }}^T}{\bf{x}} + b\\
= \sum\limits_{i = 1}^m {{\alpha _i}{y_i}{{\bf{x}}^T}{\bf{x}} + b}
\end{array}$
从对偶优化问题解出$\alpha_i$,对应着每一个样本$({{\bf{x}}_i},y_i)$,和它满足的约束。满足KKT条件,
$\left\{ {\begin{array}{*{20}{c}}
{{\alpha _i} \ge 0;}\\
{{y_i}f({{\bf{x}}_i}) - 1 \ge 0;}\\
{{\alpha _i}({y_i}f({{\bf{x}}_i}) - 1) = 0.}
\end{array}} \right.$
所以,对于任意训练样本$({{\bf{x}}_i},y_i)$,总有$\alpha _i=0$或${y_i}f({{\bf{x}}_i})=1$。若$\alpha _i=0$,则该样本不会在$\bf{\omega }$求和模型中出现,不会对$f({\bf{x}})$有任何影响; 若$\alpha _i>0$,则必有${y_i}f({{\bf{x}}_i})=1$,所对应的样本点位于最大间隔边界上,是一个支持向量。这显示出支持向量机的一个重要性质:训练完成后?大部分的训练样本都不需保留,最终模型仅与支持向量有关 。
那么如何求解${\bf{\alpha }} = ({\alpha _1};{\alpha _2},...,{\alpha _m})$呢,这里介绍一个高效算法,SMO
SMO 的基本思路是先固定$\alpha _i$之外的所有参数,然后求$\alpha _i$上的极值。由于存在约束$\sum\limits_{i = 1}^m {{\alpha _i}{y_i}} = 0$,若固定$\alpha _i$之外的其他变量,则 $\alpha _i$可由其他变量导出,所以SMO每次选择两个变量$\alpha _i$和$\alpha _j$,并固定其他参数。这样,在参数初始化后, SMO 不断执行如下两个步骤直至收敛:
标签:初始 优化问题 影响 学习 初始化 smo max 高效算法 线性
原文地址:https://www.cnblogs.com/yijuncheng/p/9977701.html