标签:输出 所有结点 层次遍历 队列 n+1 条件 广度优先 root alt
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。二叉树是每个结点最多有两个子树的树结构。它有五种基本形态:二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。
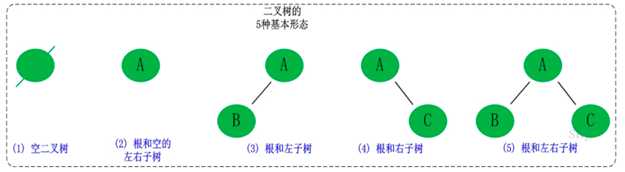
1. 二叉树的分类
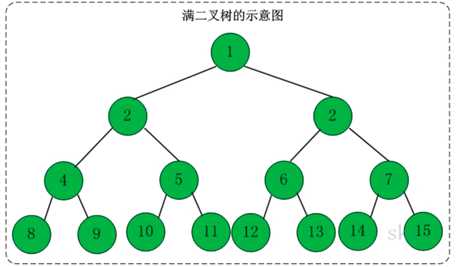
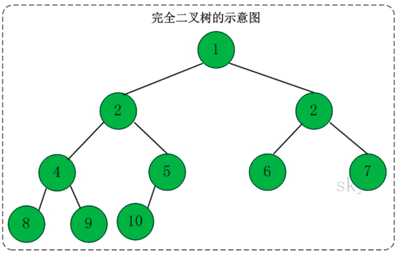
举例:

1 面试题:如果一个完全二叉树的结点总数为768个,求叶子结点的个数。 2 由二叉树的性质知:n0=n2+1,将之带入768=n0+n1+n2中得:768=n1+2n2+1,因为完全二叉树度为1的结点个数要么为0,要么为1,那么就把n1=0或者1都代入公式中,很容易发现n1=1才符合条件。所以算出来n2=383,所以叶子结点个数n0=n2+1=384。 3 4 总结规律:如果一棵完全二叉树的结点总数为n,那么叶子结点等于n/2(当n为偶数时)或者(n+1)/2(当n为奇数时)
2. 二叉树的性质
性质1:二叉树第i层上的结点数目最多为2i-1(i>=1)
性质2:深度为k的二叉树至多有2k-1个结点(k>=1)
性质3:包含n个结点的二叉树的高度至少为(log2n)+1
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
3. 二叉树的用途
(1)可以用作二叉查找树(也叫二叉搜索树):设x为二叉查找树中的一个结点,x结点包含关键字key,结点x的key值计为key[x]。如果y是x的左子树中的一个结点,则key[y]<=key[x];如果y是x的右子树的一个结点,则key[y]>=key[x]
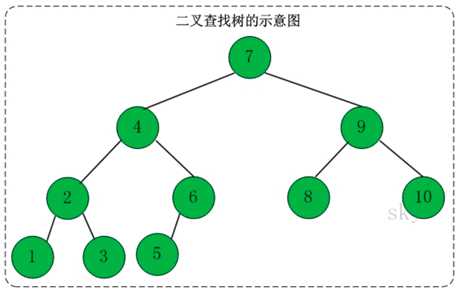
note:在二叉查找树中有以下性质:
结点的度:结点拥有的子树的数目. 与图论中的“度”不同,树的度是如下定义的:有根树T中,结点x的子女数目称为x的度。也就是:在树中,结点有几个分叉,度就是几
一个有用的小公式:树中结点数 = 总分叉数 +1。(这里的分叉数就是所有结点的度之和)
叶子结点:度为0的结点
分支结点:度不为0的结点
树的度:树中结点的最大的度
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1-----(同深度)
树的高度:树中结点的最大层次。从下往上数,最下面是高度为1
树的深度:从上往下数,最上面根部分是深度为1
森林:0个或多个不相交的树组成。对森林加上一个根,森林即成为树;删去根,树即成为森林。
举例:

1 设树T的度为4,其中度为1,2,3,4的节点个数分别为4,2,1,1,则T中的叶子数为? 2 3 解答: 4 叶子的度数为0;那么设叶子数为x,则此树的总分叉数为1*4+2*2+3*1+4*1=15;此树的节点个数为16(此处涉及到一个公式;节点数=分叉数+1,由图形便可以观察出来)。又根据题目可以知道顶点数目还可以列出一个式子:4+2+1+1+x便可以得到等式:4+2+1+1+x=16;x=8为叶子数。 5 因为此题是数据结构中的问题:一般情况下都是有向树,所以叶子节点的度数为0,要区分于离散数学中的无向树叶子节点度为一。在数据结构中一般常用的公式为:二叉树:度为0的节点数=度为2的节点数+1(n0=n2+1)此公式可由上述计算思想推导(一般在二叉树那里的公式多一些,树中只要你明确定义,画出图来,便可以根据图形寻找出规律来)
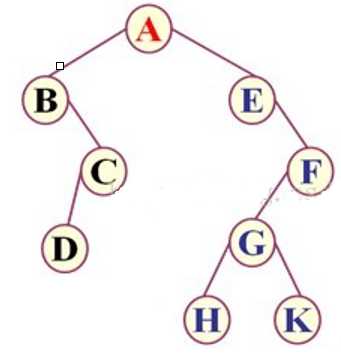
比如:上面的二叉树三种方式遍历后的情况是:
先序遍历:ABCDEFGHK
中序遍历:BDCAEHGKF
后序遍历:DCBHKGFEA
前三种遍历方式的递归代码:

1 //后序遍历,左=》右=》根 2 public void postorder_Traversal(TreeNode root) 3 { 4 if(root==null)return; 5 postorder_Traversal(root.left); 6 postorder_Traversal(root.right); 7 8 //访问节点的逻辑代码块 9 System.out.print(root.val+" "); 10 } 11 //前序遍历,根=》左=》右 12 public void preorder_Traversal(TreeNode root) 13 { 14 if(root==null)return; 15 16 //访问节点的逻辑代码块 17 System.out.print(root.val+" "); 18 19 preorder_Traversal(root.left); 20 preorder_Traversal(root.right); 21 } 22 //中序遍历,左=》根=》右 23 public void inorder_Traversal(TreeNode root) 24 { 25 if(root==null)return; 26 inorder_Traversal(root.left); 27 28 //访问节点的逻辑代码块 29 System.out.print(root.val+" "); 30 31 inorder_Traversal(root.right); 32 }
层次遍历思想:
根据层次遍历的顺序,每一层都是从左到右的遍历输出,借助于一个队列。
先将根节点入队,当前节点是队头节点,将其出队并访问,如果当前节点的左节点不为空将左节点入队,如果当前节点的右节点不为空将其入队。所以出队顺序也是从左到右依次出队。

1 import java.util.LinkedList; 2 3 public class LevelOrder 4 { 5 public void levelIterator(BiTree root) 6 { 7 if(root == null) 8 { 9 return ; 10 } 11 LinkedList<BiTree> queue = new LinkedList<BiTree>(); 12 BiTree current = null; 13 queue.offer(root);//将根节点入队 14 while(!queue.isEmpty()) 15 { 16 current = queue.poll();//出队队头元素并访问 17 System.out.print(current.val +"-->"); 18 if(current.left != null)//如果当前节点的左节点不为空入队 19 { 20 queue.offer(current.left); 21 } 22 if(current.right != null)//如果当前节点的右节点不为空,把右节点入队 23 { 24 queue.offer(current.right); 25 } 26 } 27 28 } 29 30 }
note:上面的root应该代表了整棵树
或者:

1 public static void levelRead(TreeNode root) 2 { 3 if(root == null) return; 4 Queue<TreeNode> queue = new LinkedList<TreeNode>() ; 5 queue.add(root); 6 while(queue.size() != 0) 7 { 8 int len = queue.size(); 9 for(int i=0;i <len; i++) 10 { 11 TreeNode temp = queue.poll(); 12 System.out.print(temp.val+" "); 13 if(temp.left != null) queue.add(temp.left); 14 if(temp.right != null) queue.add(temp.right); 15 } 16 } 17 }
note:poll是取出并且移除队列的头结点;peek是取出但是并不移除队列的头节点;offer将元素加入到队列的末尾;
标签:输出 所有结点 层次遍历 队列 n+1 条件 广度优先 root alt
原文地址:https://www.cnblogs.com/Hermioner/p/9963733.html