标签:复杂度 二叉树 中序遍历 算法 后序遍历 targe 中序 数据 image
数据结构——树
定义:树是一个n(n>=0)个结点的有序合集
名词理解:
结点:指树中的一个元素;
结点的度:指结点拥有的子树的个数,二叉树的度不大于2;
数的度:指树中的最大结点度数;
叶子:度为0的结点,也称为终端结点;
高度:叶子节点的高度为1,根节点高度最高;
层:根在第一层,以此类推;
二叉树的定义:由一个结点和两颗互不相交、分别称为这个根的左子树和右子树的二叉树构成(递归定义)
二叉树的性质:
1:二叉树的第i层上至多有2^(i-1)个结点
2:深度为k的二叉树,至多有2^k-1个结点
满二叉树:叶子节点一定要在最后一层,并且所有非叶子节点都存在左孩子和右孩子;
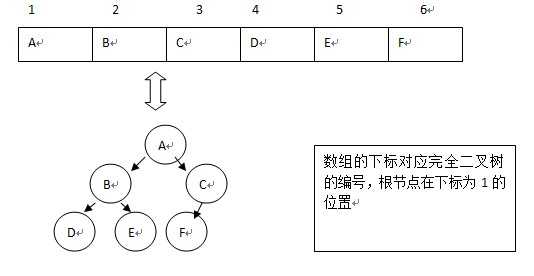
最特别的二叉树:完全二叉树:从左到右、从上到下构建的二叉树;
完全二叉树的性质:
1:结点 i 的子结点为2*i 和 2*i+1(前提是都小于总结点数)
2:结点 i 的父结点为 i/2
二叉树的遍历(要有递归的思想!!!):
1:先序遍历:根->左子树->右子树(先序)
2:中序遍历:左子树->根->右子树(中序)
3:后序遍历:左子树->右子树->根(后序)
这三种遍历方法只是访问结点的时机不同,访问结点的路径都是一样的,时间和空间复杂度皆为O(n)
二叉树的存储结构:
1:顺序存储(只适用于完全二叉树)——可以用于排序算法中的堆排序
2:链式存储(最普遍的存储方式)——由于结点可能为空,所以会比较浪费空间

如果有n个节点,则有2n个left、right指针,但是用到的只有n-1个指针
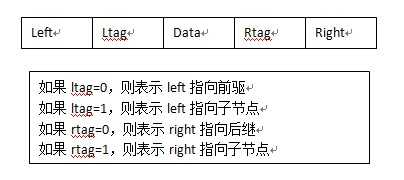
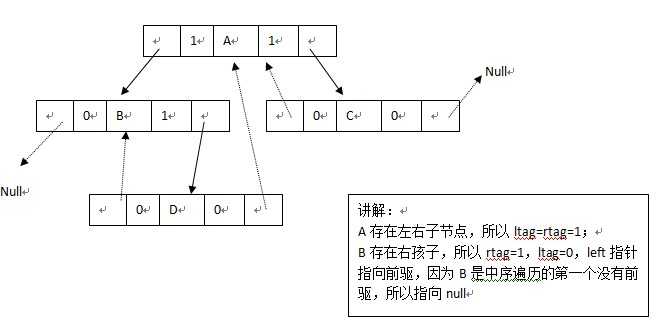
3:线索存储(改进的方法)
关于霍夫曼编码(Huffman编码):
Huffman是一种前缀编码;Huffman编码是建立在Huffman树的基础上进行的,因此为了进行Huffman编码,必须先构建Huffman树;树的路径长度是每个叶节点到根节点的路径之和;带权路径长度是(每个叶节点的路径长度*wi)之和;Huffman树是最小带权路径长度的二叉树;
构造Huffman树的过程:
(1)将各个节点按照权重从小到大排序;
(2)取最小权重的两个节点,并新建一个父节点作为这两个节点的双亲,双亲节点的权重为子节点权重之和,再将此父节点放入原来的队列;
(3)重复(2)的步骤,直到队列中只有一个节点,此节点为根节点;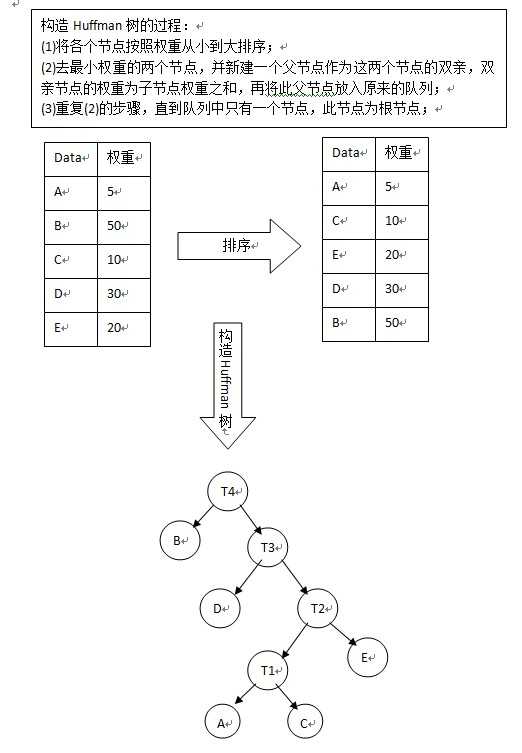
构造完Huffman树之后,就可以进行Huffman编码了,编码规则:左分支填0,右分支填1;
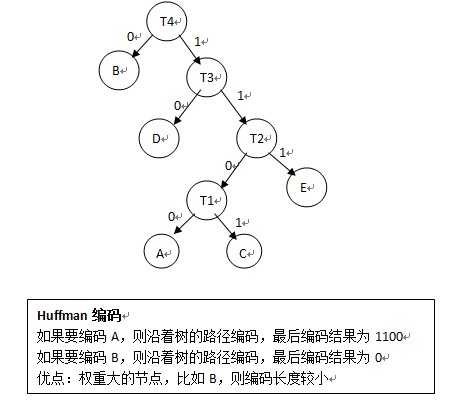
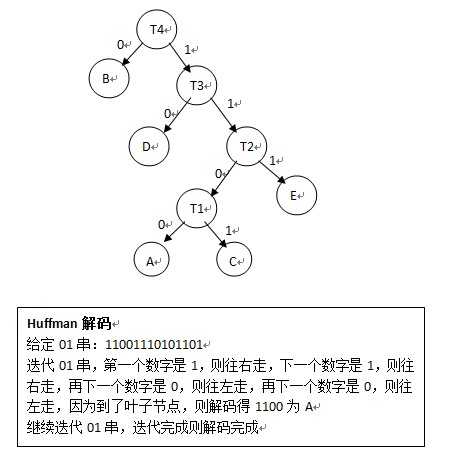
Huffman解码过程:给定一个01串,将01串进行Huffman树,到叶子节点了就表明已经解码一个节点,然后再次遍历Huffman树;
标签:复杂度 二叉树 中序遍历 算法 后序遍历 targe 中序 数据 image
原文地址:https://www.cnblogs.com/Stephen-Jixing/p/10011085.html