标签:first array time mat graphic .com lov fan 区间
Petya is having a party soon, and he has decided to invite his nn friends.
He wants to make invitations in the form of origami. For each invitation, he needs two red sheets, five green sheets, and eight blue sheets. The store sells an infinite number of notebooks of each color, but each notebook consists of only one color with kk sheets. That is, each notebook contains kk sheets of either red, green, or blue.
Find the minimum number of notebooks that Petya needs to buy to invite all nn of his friends.
The first line contains two integers nn and kk (1≤n,k≤1081≤n,k≤108) — the number of Petya‘s friends and the number of sheets in each notebook respectively.
Print one number — the minimum number of notebooks that Petya needs to buy.
3 5
10
15 6
38
In the first example, we need 22 red notebooks, 33 green notebooks, and 55 blue notebooks.
In the second example, we need 55 red notebooks, 1313 green notebooks, and 2020 blue notebooks.
题解:水题;向上取证即可;
参考代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define cls(x, val) memset(x,val,sizeof(x)) 4 typedef long long ll; 5 typedef unsigned long long ull; 6 const int INf=0x3f3f3f3f; 7 double n,k,n1,n2,n3; 8 int main() 9 { 10 scanf("%lf%lf",&n,&k); 11 n1=2*n,n2=5*n,n3=8*n; 12 int sum=ceil(n1/k)+ceil(n2/k)+ceil(n3/k); 13 printf("%d\n",sum); 14 15 return 0; 16 }
Little girl Margarita is a big fan of competitive programming. She especially loves problems about arrays and queries on them.
Recently, she was presented with an array aa of the size of 109109 elements that is filled as follows:
That is, the value of the ii-th element of the array aa is calculated using the formula ai=i⋅(−1)iai=i⋅(−1)i.
She immediately came up with qq queries on this array. Each query is described with two numbers: ll and rr. The answer to a query is the sum of all the elements of the array at positions from ll to rr inclusive.
Margarita really wants to know the answer to each of the requests. She doesn‘t want to count all this manually, but unfortunately, she couldn‘t write the program that solves the problem either. She has turned to you — the best programmer.
Help her find the answers!
The first line contains a single integer qq (1≤q≤1031≤q≤103) — the number of the queries.
Each of the next qq lines contains two integers ll and rr (1≤l≤r≤1091≤l≤r≤109) — the descriptions of the queries.
Print qq lines, each containing one number — the answer to the query.
5 1 3 2 5 5 5 4 4 2 3
-2 -2 -5 4 -1
In the first query, you need to find the sum of the elements of the array from position 11 to position 33. The sum is equal to a1+a2+a3=−1+2−3=−2a1+a2+a3=−1+2−3=−2.
In the second query, you need to find the sum of the elements of the array from position 22 to position 55. The sum is equal to a2+a3+a4+a5=2−3+4−5=−2a2+a3+a4+a5=2−3+4−5=−2.
In the third query, you need to find the sum of the elements of the array from position 55 to position 55. The sum is equal to a5=−5a5=−5.
In the fourth query, you need to find the sum of the elements of the array from position 44 to position 44. The sum is equal to a4=4a4=4.
In the fifth query, you need to find the sum of the elements of the array from position 22 to position 33. The sum is equal to a2+a3=2−3=−1a2+a3=2−3=−1.
题解:水题,就是求数组的区间和,数组:奇数为负,偶数为正;先判断是奇数开头还是偶数开头,然后除2*1(奇数*-1),然后判断(r-l+1)是奇数还是偶数,然后最后一个元素特判即可;
参考代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define cls(x, val) memset(x,val,sizeof(x)) 4 typedef long long ll; 5 typedef unsigned long long ull; 6 const int INf=0x3f3f3f3f; 7 int n,l,r; 8 int main() 9 { 10 scanf("%d",&n); 11 while(n--) 12 { 13 int sum; 14 scanf("%d%d",&l,&r); 15 if(l%2) 16 { 17 int num=(r-l+1)/2,temp=(r-l+1)%2; 18 sum=num+temp*(-r); 19 } 20 else 21 { 22 int num=(r-l+1)/2,temp=(r-l+1)%2; 23 sum=-num+temp*r; 24 } 25 printf("%d\n",sum); 26 } 27 28 return 0; 29 }
Recently, Masha was presented with a chessboard with a height of nn and a width of mm.
The rows on the chessboard are numbered from 11 to nn from bottom to top. The columns are numbered from 11 to mm from left to right. Therefore, each cell can be specified with the coordinates (x,y)(x,y), where xx is the column number, and yy is the row number (do not mix up).
Let us call a rectangle with coordinates (a,b,c,d)(a,b,c,d) a rectangle lower left point of which has coordinates (a,b)(a,b), and the upper right one — (c,d)(c,d).
The chessboard is painted black and white as follows:
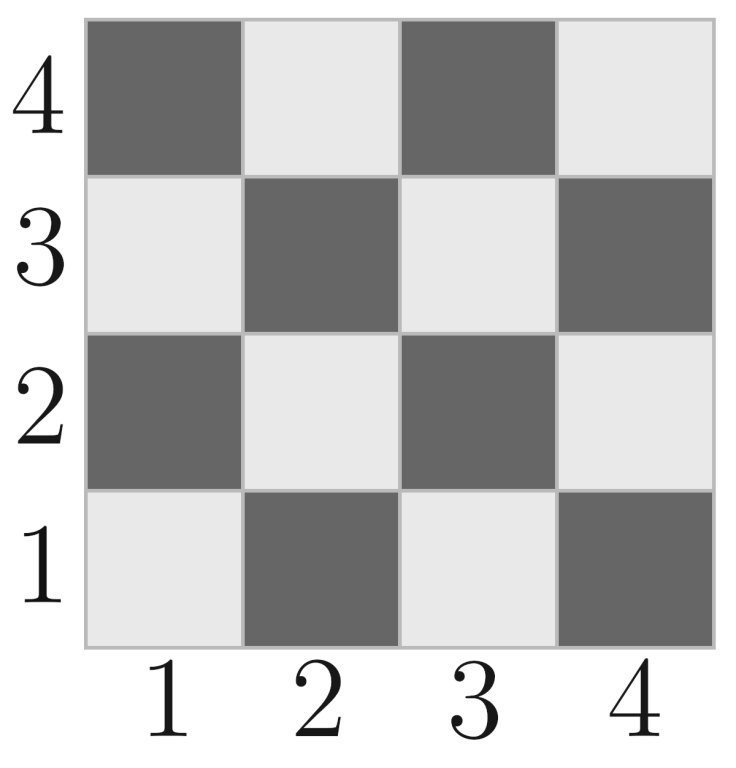
Masha was very happy with the gift and, therefore, invited her friends Maxim and Denis to show off. The guys decided to make her a treat — they bought her a can of white and a can of black paint, so that if the old board deteriorates, it can be repainted. When they came to Masha, something unpleasant happened: first, Maxim went over the threshold and spilled white paint on the rectangle (x1,y1,x2,y2)(x1,y1,x2,y2). Then after him Denis spilled black paint on the rectangle (x3,y3,x4,y4)(x3,y3,x4,y4).
To spill paint of color colorcolor onto a certain rectangle means that all the cells that belong to the given rectangle become colorcolor. The cell dyeing is superimposed on each other (if at first some cell is spilled with white paint and then with black one, then its color will be black).
Masha was shocked! She drove away from the guests and decided to find out how spoiled the gift was. For this, she needs to know the number of cells of white and black color. Help her find these numbers!
The first line contains a single integer tt (1≤t≤1031≤t≤103) — the number of test cases.
Each of them is described in the following format:
The first line contains two integers nn and mm (1≤n,m≤1091≤n,m≤109) — the size of the board.
The second line contains four integers x1x1, y1y1, x2x2, y2y2 (1≤x1≤x2≤m,1≤y1≤y2≤n1≤x1≤x2≤m,1≤y1≤y2≤n) — the coordinates of the rectangle, the white paint was spilled on.
The third line contains four integers x3x3, y3y3, x4x4, y4y4 (1≤x3≤x4≤m,1≤y3≤y4≤n1≤x3≤x4≤m,1≤y3≤y4≤n) — the coordinates of the rectangle, the black paint was spilled on.
Output tt lines, each of which contains two numbers — the number of white and black cells after spilling paint, respectively.
5 2 2 1 1 2 2 1 1 2 2 3 4 2 2 3 2 3 1 4 3 1 5 1 1 5 1 3 1 5 1 4 4 1 1 4 2 1 3 4 4 3 4 1 2 4 2 2 1 3 3
0 4 3 9 2 3 8 8 4 8
Explanation for examples:
The first picture of each illustration shows how the field looked before the dyes were spilled. The second picture of each illustration shows how the field looked after Maxim spoiled white dye (the rectangle on which the dye was spilled is highlighted with red). The third picture in each illustration shows how the field looked after Denis spoiled black dye (the rectangle on which the dye was spilled is highlighted with red).
In the first test, the paint on the field changed as follows:
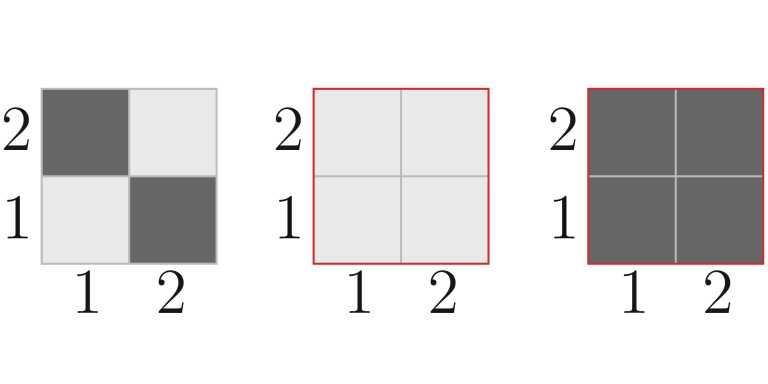
In the second test, the paint on the field changed as follows:
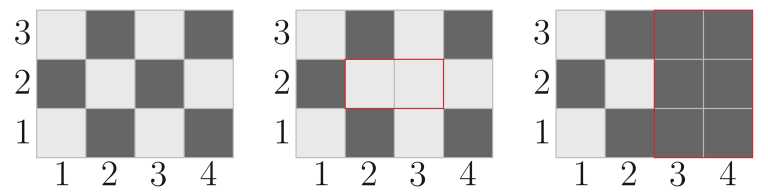
In the third test, the paint on the field changed as follows:
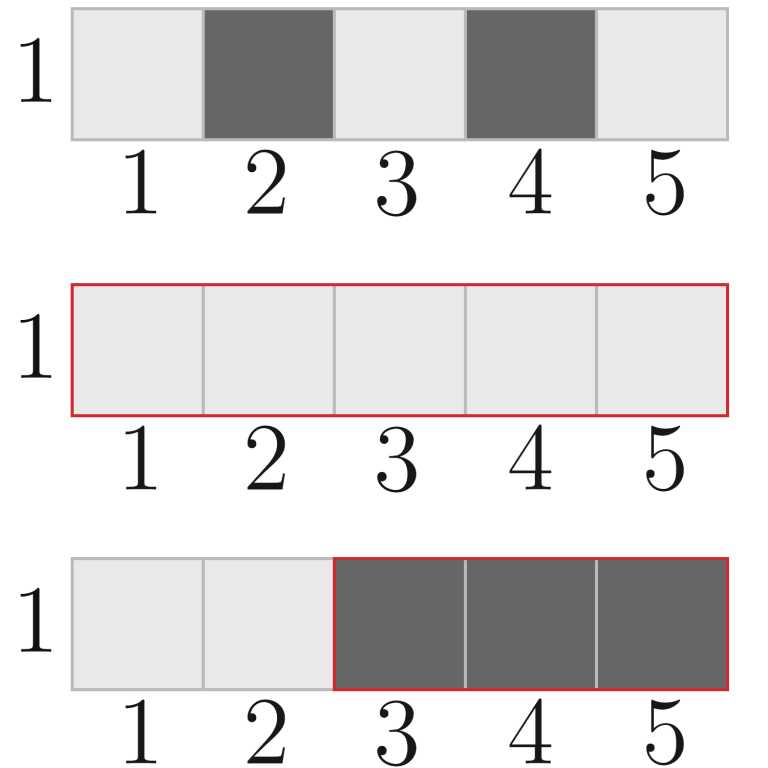
In the fourth test, the paint on the field changed as follows:
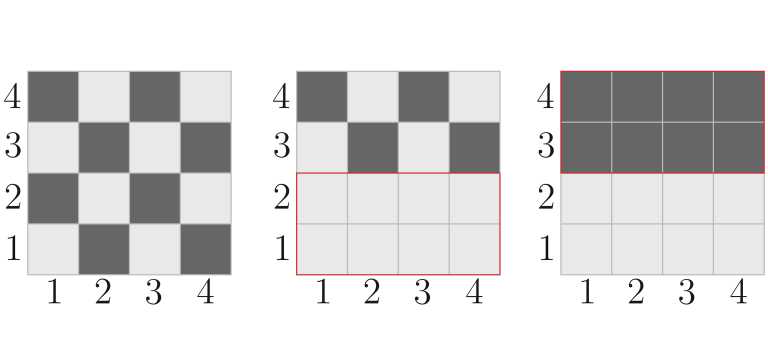
In the fifth test, the paint on the field changed as follows:
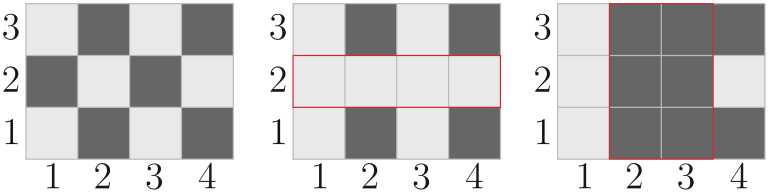
题意:题意给你一个n*m个矩形,里面有n*m个黑白色的小方块,分布如图所给的那样,然后划分区间将其全部变为白色,然后再划一个区间,将其全部变为黑色,
然后让你求,最后黑色白色的个数;
题解:(暴力肯定不行的),我们首先计算出划分第一个区间时,计算出白色的增加量ans+=cnt,然后再判断两个划分区间是否相交,如果相交,我们先将第一次划分中的黑色
变为白色的恢复成黑色,(就是白色的数量减去相交部分黑色的数量),然后我们计算第二次划分白色减少的数量,ans-=cnt1;就得到了最终白色的数量,则sum-ans即为黑色的数量。
(注意开long long)窝就是没开long long WA了一发,这一题只要仔细分析,代码认真就没啥问题Orz;
参考代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define cls(x, val) memset(x,val,sizeof(x)) 4 typedef long long ll; 5 typedef unsigned long long ull; 6 const int INf=0x3f3f3f3f; 7 ll T,n,m,l1,r1,l2,r2,x1,x2,y,y2; 8 int main() 9 { 10 scanf("%lld",&T); 11 while(T--) 12 { 13 scanf("%lld%lld",&n,&m); 14 scanf("%lld%lld%lld%lld",&l1,&r1,&l2,&r2); 15 scanf("%lld%lld%lld%lld",&x1,&y,&x2,&y2); 16 ll ans1=n*m/2;//black 17 ll ans2=n*m-ans1;//white 18 if(((l2-l1+1)&1) && ((r2-r1+1)&1)) 19 { 20 if((l1&1)&&(r1&1) || (!(l1&1))&&(!(r1&1))) ans2+=(r2-r1+1)*(l2-l1+1)/2; 21 else ans2+=(r2-r1+1)*(l2-l1+1)/2+(r2-r1+1)*(l2-l1+1)%2; 22 } 23 else ans2+=(r2-r1+1)*(l2-l1+1)/2; 24 if(!(x2<l1 || y2<r1 || l2<x1 || r2<y) ) 25 { 26 ll cx=max(l1,x1),cy=max(r1,y); 27 ll ccx=min(l2,x2),ccy=min(r2,y2); 28 if((cx&1)&&(cy&1) || (!(cx&1)) && (!(cy&1))) ans2-=(ccx-cx+1)*(ccy-cy+1)/2; 29 else ans2-=(ccx-cx+1)*(ccy-cy+1)/2+(ccx-cx+1)*(ccy-cy+1)%2; 30 } 31 if(((x2-x1+1)&1) && ((y2-y+1)&1)) 32 { 33 if((x1&1)&&(y&1) || (!(x1&1))&&(!(y&1))) 34 ans2-=(y2-y+1)*(x2-x1+1)/2+(y2-y+1)*(x2-x1+1)%2; 35 else ans2-=(y2-y+1)*(x2-x1+1)/2; 36 } 37 else ans2-=(y2-y+1)*(x2-x1+1)/2; 38 printf("%lld %lld\n",ans2,n*m-ans2); 39 } 40 return 0; 41 }
Recently, Olya received a magical square with the size of 2n×2n2n×2n.
It seems to her sister that one square is boring. Therefore, she asked Olya to perform exactly kk splitting operations.
A Splitting operation is an operation during which Olya takes a square with side aa and cuts it into 4 equal squares with side a2a2. If the side of the square is equal to 11, then it is impossible to apply a splitting operation to it (see examples for better understanding).
Olya is happy to fulfill her sister‘s request, but she also wants the condition of Olya‘s happiness to be satisfied after all operations.
The condition of Olya‘s happiness will be satisfied if the following statement is fulfilled:
Let the length of the side of the lower left square be equal to aa, then the length of the side of the right upper square should also be equal to aa. There should also be a path between them that consists only of squares with the side of length aa. All consecutive squares on a path should have a common side.
Obviously, as long as we have one square, these conditions are met. So Olya is ready to fulfill her sister‘s request only under the condition that she is satisfied too. Tell her: is it possible to perform exactly kk splitting operations in a certain order so that the condition of Olya‘s happiness is satisfied? If it is possible, tell also the size of the side of squares of which the path from the lower left square to the upper right one will consist.
The first line contains one integer tt (1≤t≤1031≤t≤103) — the number of tests.
Each of the following tt lines contains two integers nini and kiki (1≤ni≤109,1≤ki≤10181≤ni≤109,1≤ki≤1018) — the description of the ii-th test, which means that initially Olya‘s square has size of 2ni×2ni2ni×2ni and Olya‘s sister asks her to do exactly kiki splitting operations.
Print tt lines, where in the ii-th line you should output "YES" if it is possible to perform kiki splitting operations in the ii-th test in such a way that the condition of Olya‘s happiness is satisfied or print "NO" otherwise. If you printed "YES", then also print the log2log2 of the length of the side of the squares through space, along which you can build a path from the lower left square to the upper right one.
You can output each letter in any case (lower or upper).
If there are multiple answers, print any.
3 1 1 2 2 2 12
YES 0 YES 1 NO
In each of the illustrations, the pictures are shown in order in which Olya applied the operations. The recently-created squares are highlighted with red.
In the first test, Olya can apply splitting operations in the following order:
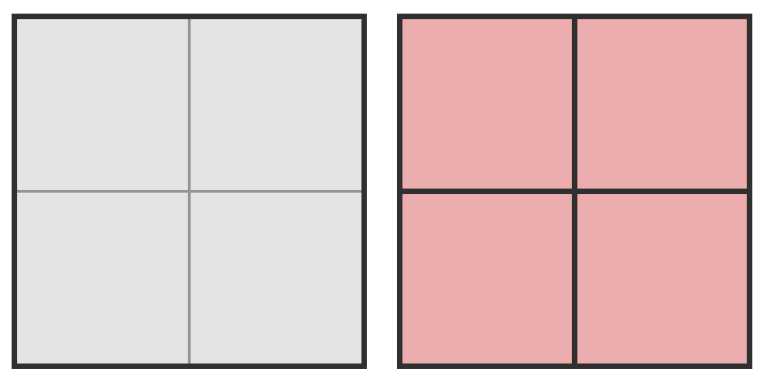
The condition of Olya‘s happiness will be met, since there is a path of squares of the same size from the lower left square to the upper right one:
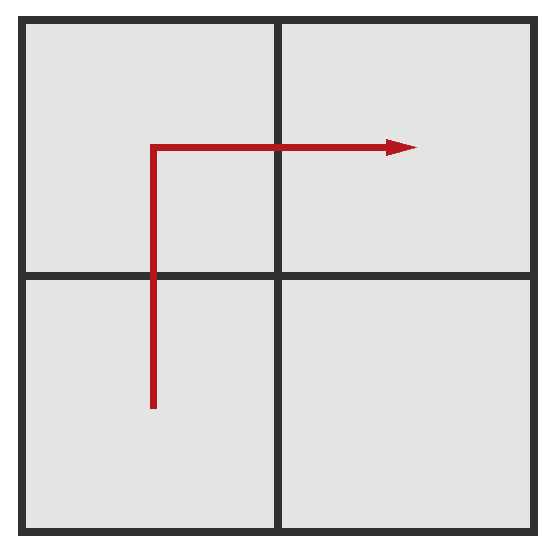
The length of the sides of the squares on the path is 11. log2(1)=0log2(1)=0.
In the second test, Olya can apply splitting operations in the following order:
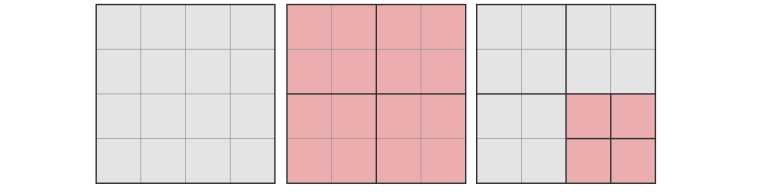
Olya applies the first operation on the only existing square. She applies the second one on the right bottom square.
The condition of Olya‘s happiness will be met, since there is a path of squares of the same size from the lower left square to the upper right one:
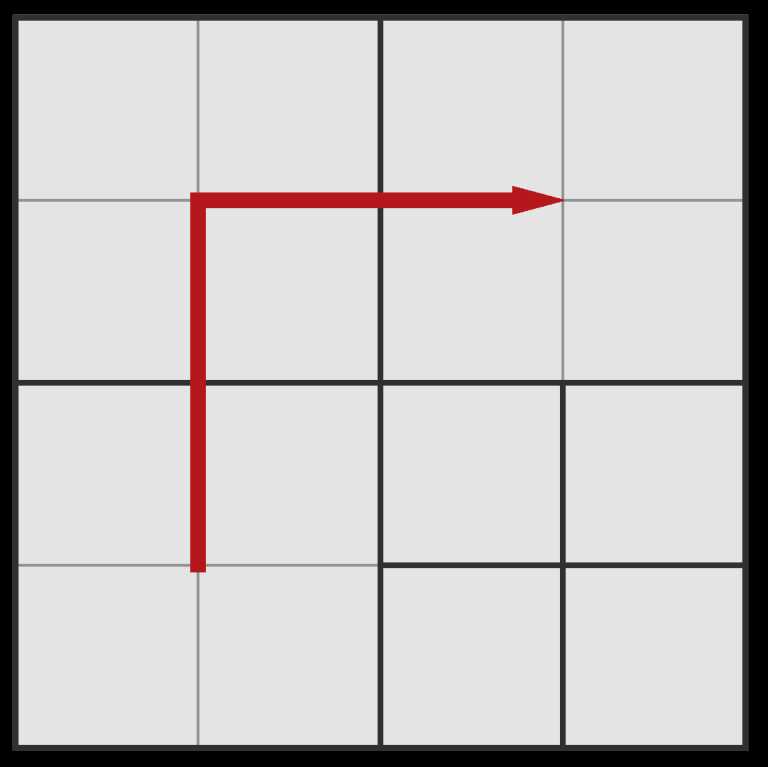
The length of the sides of the squares on the path is 22. log2(2)=1log2(2)=1.
In the third test, it takes 55 operations for Olya to make the square look like this:
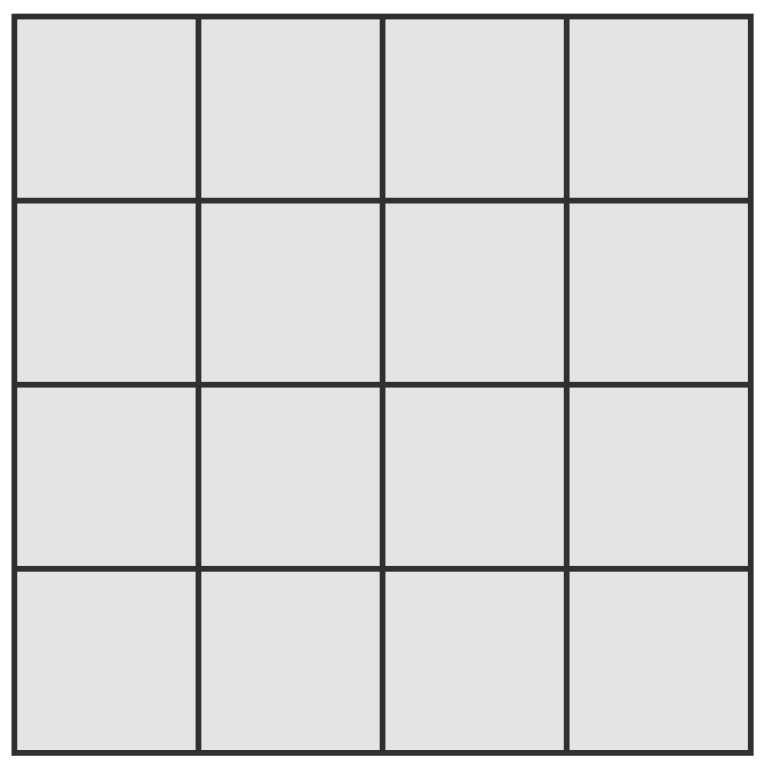
Since it requires her to perform 77 splitting operations, and it is impossible to perform them on squares with side equal to 11, then Olya cannot do anything more and the answer is "NO".
题意:给你一个2^n*2^n的方块,每一次选一个正方形把他分成四块,一共k步问最后是否可以让最后的左下角方块的大小等于右上角方块的大小,而且可以从左下角沿着同样大小的方块走到右上角.
题解:
最后的路径一定可以是沿着边界走到右上角,只要路径上大小固定,就可以算出其它块可以分裂的次数,所以只要动态维护当前分裂次数a和可以分裂的次数b,如果当前分裂次数已经>k则不满足,否则如果出现a<=k&&a+b>=k说明有满足情况的答案。
动态维护分裂的过程需要维护好多个变量,首先要维护路径的长度,这样也就知道去除路径剩多少个可分裂的块。还要维护左下角块的大小,也就知道可分裂次数。之后动态维护a,b就可以了。
参考代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 long long n,k; 4 int main() 5 { 6 long long T;cin>>T; 7 while(T--) 8 { 9 cin>>n>>k; 10 long long cnt=1,tmp=n; 11 while(cnt<=k&&tmp) 12 { 13 --tmp; k-=cnt; 14 cnt=2*cnt+1; 15 } 16 for(long long sl=1,x=n-1;x>=tmp;--x,sl=sl*2+3) 17 { 18 for(long long tmp2=x,cnt2=1;tmp2&&k>0;--tmp2,cnt2*=4) k-=sl*cnt2; 19 if(k<=0) break; 20 } 21 if(k>0) cout<<"NO"<<endl; 22 else cout<<"YES"<<‘ ‘<<tmp<<endl; 23 } 24 return 0; 25 }
菜鸡就只会写4题,QwQ.
后面两题挖坑...
标签:first array time mat graphic .com lov fan 区间
原文地址:https://www.cnblogs.com/songorz/p/10014497.html