五子棋项目的实现（三）人机对战类的具体设计

标签：最大   个数   max   二维数组   arrays   维数   http   设计   节点   

在之前描述了博弈树算法的思想，现在则是关键类的设计实现。在具体的过程中我们先要设计一个遍历棋型算法，来遍历整个棋盘中的各种棋型

通过最后返回值的不同，来确定不同的棋型

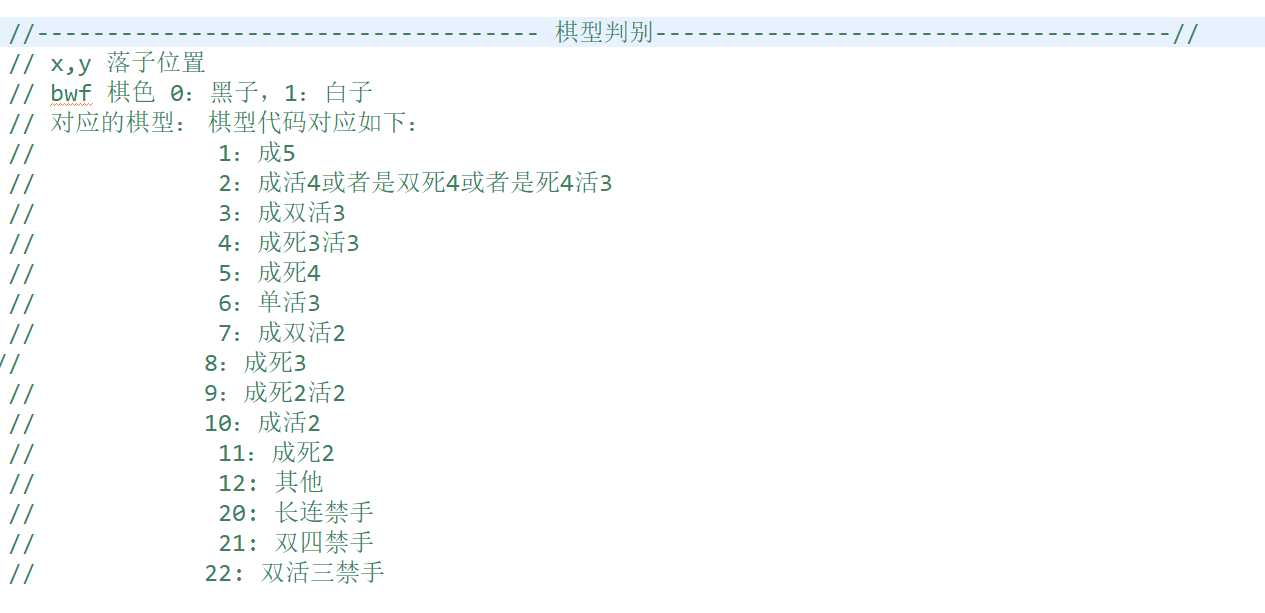
当中有评估函数对当前的棋型进行打分。再选取局部最优的几个落子点作为下一步扩展的节点。

//bwf 棋色 0：黑棋 1：白棋
//return 选出来的节点坐标
private int[][] getBests(int bwf) {//传过来的还是颜色

int i_min=(x_min==0 ? x_min:x_min-1);//x为真则是b值否则就是c值
int j_min=(y_min==0 ? y_min:y_min-1);
int i_max=(x_max==15 ? x_max:x_max+1);
int j_max=(y_max==15 ? y_max:y_max+1);
int n = 0;
int type_1,type_2;
int[][] rt = new int[(i_max-i_min) * (j_max-j_min)][3];//确定一个数组的大小
for ( int i = i_min; i < i_max; i++)
for (int j = j_min; j < j_max; j++)//循环的形式遍历周围最大最小值的位置
if (isChessOn[i][j] == 2) {
type_1 = getType(i, j, bwf);
type_2 = getType(i, j, 1 - bwf);
if(able_flag && bwf==0 && (type_1 == 20 || type_1 == 21 || type_1 == 22)) // 禁手棋位置,不记录
continue;
rt[n][0] = i;
rt[n][1] = j;
rt[n][2] = getMark(type_1) + getMark(type_2);
n++;
}
// 对二维数组排序
Arrays.sort(rt, new ArrComparator());
int size = weight > n? n:weight;
int[][] bests = new int[size][3];
System.arraycopy(rt, 0, bests, 0, size);
return bests;
}

五子棋项目的实现（三）人机对战类的具体设计

标签：最大   个数   max   二维数组   arrays   维数   http   设计   节点   

原文地址：https://www.cnblogs.com/fly0512/p/10014939.html