标签：href   under   改变   产生   付出   意思   必须   技术分享   new   

目录

• Two-Finger算法
  • 前提
  • 概要
  • 步骤一：移动对象
  • 步骤二：更新指针
  • 优缺点
• 表格算法
  • 概要
  • 步骤一：移动对象群 和 构筑间隙表格
    • 移动对象群
    • 构筑间隙表格
  • 步骤二：更新指针
  • 优缺点

Two-Finger算法

Robert A.Saunders 对堆执行两次搜索

前提

Two-Finger 算法，必须将所有对象整理成大小一致。它没有在对象的头中设立forwarding指针，而是在对象的域中设立forwarding指针即可。

概要

Two-Finger算法由一下两个步骤构造。

• 移动对象
• 更新指针

在Lisp2算法中，是将对象移动到堆的一端。在Two-Finger中，操作对象向左滑动，通过执行压缩算法来填补空闲空间。此时为了让更好的填补空间，所以对象大小必须一样。

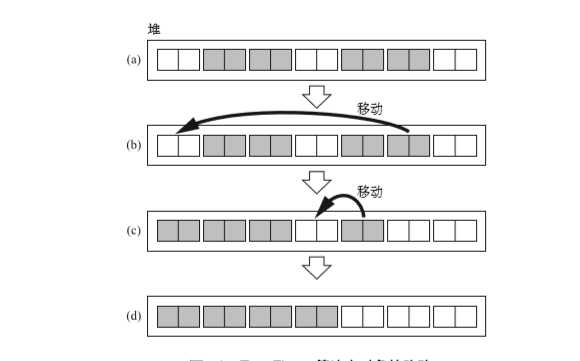
移动前的对象都会被保留（图的白色对象）。因为在Two-Finger算法中，我们要利用放置非活动对象的空间来作为活动对象的目标空间，这是为了让移动前的对象不会在GC过程中被覆盖掉。这样一来，我们就能把forwarding指针设定在这个移动前 的对象的域中，没有必要多准备出 1 个字了。

步骤一：移动对象

• $free和live两个指针，从两端向正中间搜索堆。
• $free是用于寻找非活动的指针，live是寻找活动对象(原空间)

• 两个指针发现空间和原空间的对象时会移动对象。

• 途中虚线其实表示forwarding。
• 之后使用move_obj函数对对象进行移动其伪代码如下：

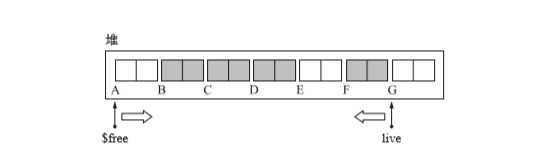
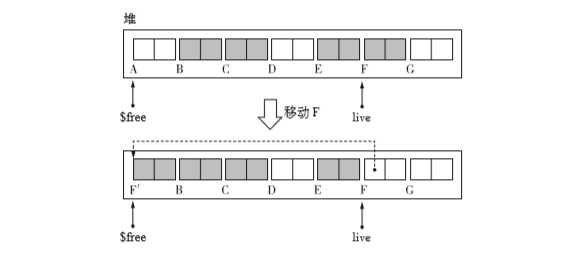
move_obj(){
    $free = $heap_start
    live = $heap_end - OBJ_SIZE
    while(TRUE)
        while($free.mark == TRUE) //从前往后寻找非活动对象
            $free += OBJ_SIZE
        while(live.mark == FLASE) // 重后往前 寻找活动对象
            live -= OBJ_SIZE
        if($free < live)   // 判断交换条件
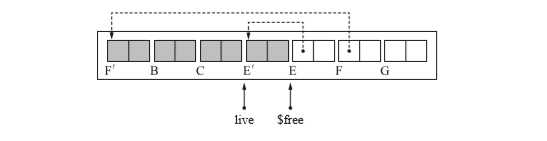
            copy_data($free, live, OBJ_SIZE)
            live.forwarding = $free
            live.mark = FALSE
        else
            break
}

• 先从前往后，使用$free寻找非活动对象。
• 在从后往前，使用live寻找活动对象。
• 找到之后，判断两者位置。如果非活动对象在活动对象之前，就执行复制操作。否则就退出循环。

步骤二：更新指针

接下来寻找指向移动前的对象的指针，把它更新，使其指向移动后的对象。更新指针操作的是adjust_ptr()函数。

• 当对象移动结束时，$free 指针指向分块的开头，这时位于 $free 指针右边的不是非活动对象就是活动对象。
• $free右边地址的指针引用的是移动前的对象。

adjust_ptr(){
    for(r :$roots)
        if(*r >= $free)
            *r = (*r).forwarding
    
    scan = $heap_start
    while(scan < $free)
        scan.mark = FALSE
        for(child :children(scan))
            if(*child >= $free)
                *child = (*child).forwarding
            scab += OBJ_SIZE
            
}

• 先查询根直接引用的对象。当这些指针的对象在$free右边的时候,就意味这个对象已经被移动到了某处。在这种情况下必须将指针的引用目标更新到移动后的对象。
• 所有活动对象都在$heap_start 和 $free之间，我们需要取遍历这一部分堆。

优缺点

优点：Two-Finger 算法能把 forwarding 指针设置在移动前的对象的域里，所以不需要额外的内存 空间以用于 forwarding 指针。只需要2次搜索堆。

缺点： Two-Finger 算法则不考虑对象间的引用关系，一律对其进行压缩，结果就导致对象的顺序在压缩前后产生了巨大的变化。因此，我们无法更好的使缓存。 对象大小必须一样。

表格算法

B.K.Haddon 和 W.M.Waite， 1967

这个算法使用表格来进行压缩，和Two-Finger一样都是执行两次压缩。

概要

表格算法通过以下2个步骤来执行压缩。

1. 移动对象以及构筑间隙表格(break table)
2. 更新指针

步骤1是让连续的活动对象群一并移动。（和前面所接触到的压缩算法都不同）。除此之外还要预留更新指针所用到的信息，这里我们使用间隙表格。

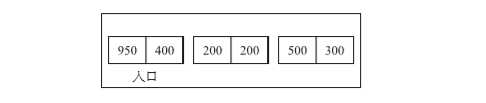
间隙表格，大概意思是“按照一个个活动对象群记录下压缩所需要的信息的表格”。这个表格事先放入移动前的对象群信息（位于对象群的首地址和较低地址的分块的总大小）。为了方便地址计算，我们将1个字的大小定为50.如下图示：

• 各个入口左边的值是活动对象群的首地址，右边的值是分块的总大小。随着对象的移动，它会被放置在空闲空间里。不过，间隙表格的各个入口需要2个字节。也就是说，这算法的其中一个限制条件就是，每个对象都必须在2个字节以上。
• 步骤2，更新每个指针。

步骤一：移动对象群 和 构筑间隙表格

移动对象群

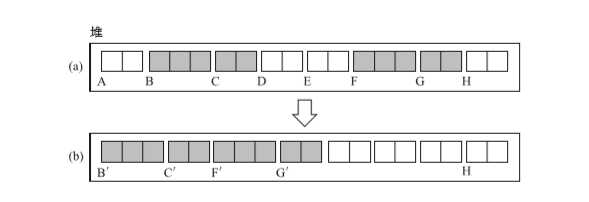
活动对象群移动前和移动后(move_obj())的状态如图示：

move_obj(){
    scan = $free = $heap_start
    size = 0
    while(scan < $heap_end)  // while 循环 1
        while(scan.mark == FALSE) 
            size += scan.size
            scan += scan.size
        live = scan
        while(scan.mark == TRUE) // while 循环 2
            scan += scan.size
        slide_objs_and_mark_bt(scan ,$free, live, size)
        $free += (scan-live)
}

• scan用于寻找活动群对象，从堆头开始搜索。
• $free是指向对象群目标空间的指针，size是保持分块大小的变量。这里的分块是指用来记录到间隙表格里的分块。
• 第一个while中，scan指针负责寻找活动对象的群的开头。也就是说，直到它寻找到活动对象为止，都会跳过非活动对象。于此同时使用size计算scan指针跳过的空间大小。
• scan是指针，size是整数。
• 搜索结束时候，scan指针指向活动对象群开头。这个为止记录在live指针里。
• 之后继续使用scan，搜索连续的多动对象群。（一次找对活动对象循环完毕）

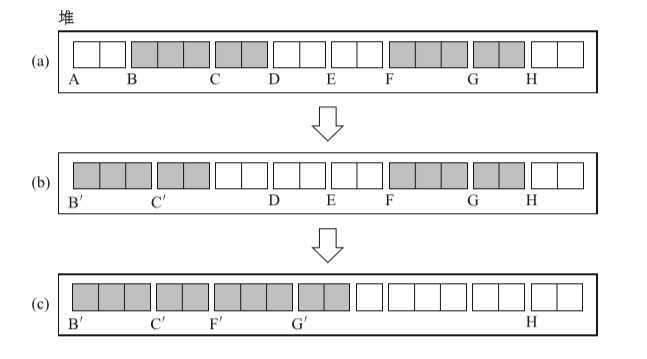
这时，堆的状态如下图示：

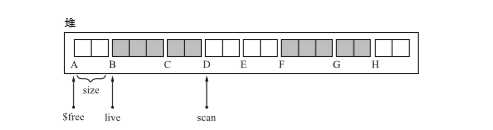
在第二个while循环中

• 其中slide_objs_and_make_bt()函数中执行活动对象群和构筑间隙表格的操作。对象群的原空间是live，目标空间是$free，要移动的对象群的总大小是scan-live。
• 最后一行，准备下一次移动，将$free移动scan-live个大小，即$free向后移动大小等于对象群的大小。如下图示：

• 这里和Lisp2算法一样，都是通过把活动对象左滑压缩。不过这里是移动连续的对象群。

构筑间隙表格

在上一个图中，每次移动对象群的时候都需要吧信息注册到间隙表格中。注册入口是对象群的首地址live和对象群滑动大小size的组合。如下图示：

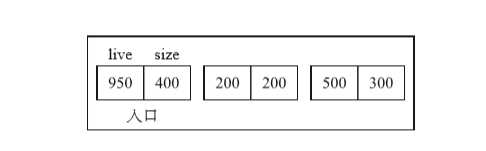
构筑间隙表格是在slide_objs_and_mark_bt()方法中指向的，下面使用图例来说明过程：

• 间隙表格构筑有以下两项操作构成。
  • 移动对象群
  • 移动间隙表格
• 下图示()内数字表格各个对象的首地址，设1个字的大小为50

• 如中a部分，在移动对象群BC的同时构筑间隙表格。将BC的首地址100以及BC最左边的分块大小100组合成一对，通过scan指针写入已知分块的350号地址。
• b部分，在这里进行的是移动对象群FG的操作。这时候要注册到间隙表的的信息是(550, 300)不过不能直接将该信息写入(100, 100)之后（450块）因为对象群要移进去。
• 这时候，我们有的间隙表格移动到FG后面也就是700号地址里。
• 完成后状态如e所示。注意间隙表格的入口顺序，各个入口不是按入口里的第一元素排列的，也就是说，不是按活动对象群的首地址live进行排列的。
  • 在b中，因为间隙表格妨碍到对象FG的移动，所以先让它回避到800,之后在移动FC将新的表格注册到了700上。
  • 像这样往已有的间隙表格中新追加入口时，会有表格左侧空闲的情况，在这种情况下，入口顺序只能乱了。
  • 当然也可以按照顺序排列，如论是在添加的时候按顺序，或者添加完之后排序，它都要花费一定的空间和时间。
• 因为没有按照第一元素live的顺序排列，所以增大了更新指针的计算量。

步骤二：更新指针

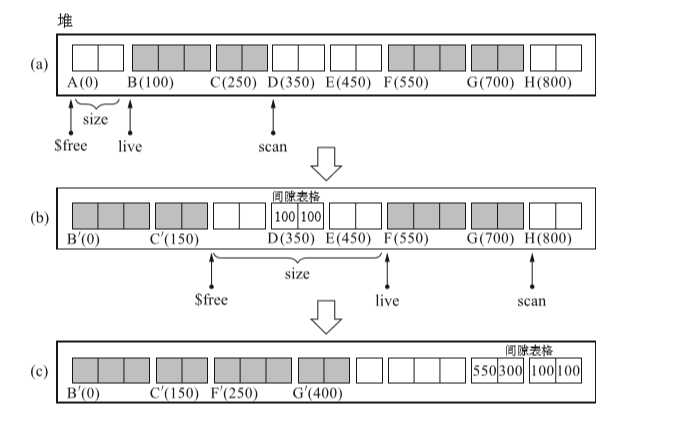
在dajust_ptr()函数中，将引用移动前的对象的指针全部换成引用移动后的对象的指针。这项操作本身和前面的两个算法中的操作是相同的。

adjust_ptr(){
    for(r :$roots)
        *r = new_address(*r)
        
    scan = $heap_start
    while(scan < $free)
        scan.mark = FALSE
        for(child : children(scan))
            *child = new_address(*child)
        scan += scan.size
        
}

下面是new_address(obj)函数

new_address(obj){
    best_entry = new_bt_entry(0, 0)
    for(entry :break_table)
        if(entry.address <= obj && $best_entry.address < entry.address)
            best_entry = entry
    return obj - best_entry.size
    
}

• 这个函数返回参数obj移动后的地址，在其中new_bt_entry(0, 0)函数中生成虚拟间隙表格的入口。
• for循环负责调查间隙表格，在持有obj及其一下地址的入口中寻找最大的入口。这样一来就得到了持有obj所属对象群信息的入口。这个入口就是best_entry
• 如果间隙表格里的入口是按照地址顺序整齐排列的，我们就有可能用二分查找有效地址查询到best_entry。但是间隙表格的入口并不是整齐排列的，因此就需要通过上面这种方式来查找。
• best_entry是一个入口，这个入口持有obj所属对象群移动前的信息。属于这个对象群的对象都会被向左移动best_entry.size个大小。因此obj移动后的地址变成了obj-best_entry.size。

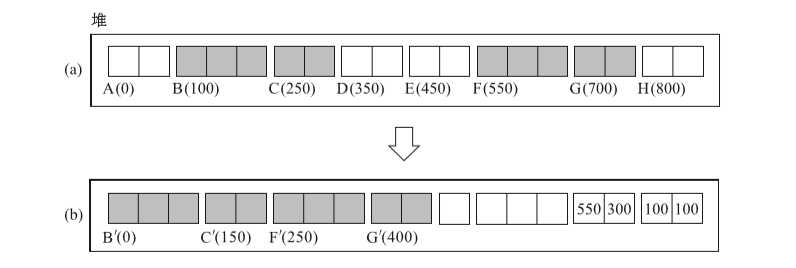
上图中如果我们想知道B移动到了B?，首先就要以B的地址100为线索调查间隙表格，然后就会发现入口（100，100）是best_entry，接下来可由B的地址 100 求得 best_entry.size，即将 B 的地址减去 100 得到 B? 的地址 0。 同理，我们可以从 F 的地址 550 减去入口（550，300）中的 300，得到 F? 的地址 250。

优缺点

优点：算法很好地利用了分块，保留了更换指针所必要的信息。（没有为压缩备出多余空间，）并且它没有改变对象的顺序，所以可以通过缓存来提高对象的访问速度。

缺点：维持间隙表格需要付出很高的代价，每次移动对象群都要对表格进行操作。

Mark Compact GC (Part two :Two-Finger)

标签：href   under   改变   产生   付出   意思   必须   技术分享   new   

原文地址：https://www.cnblogs.com/Leon-The-Professional/p/9994395.html