标签：冗余   问题   旋转矩阵   角度   优化   约束   变换   特殊   special   

第三讲：三维空间刚体运动

旋转的几种表达方式

向量

• 关于向量：

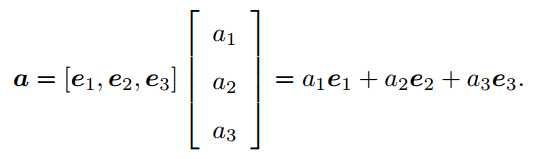
注：其中e_１，e₂，ｅ₃为线性空间下的一组基。

• 向量的内积：

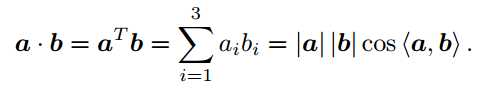
注：向量的内积表示向量间的投影关系。

• 向量的外积

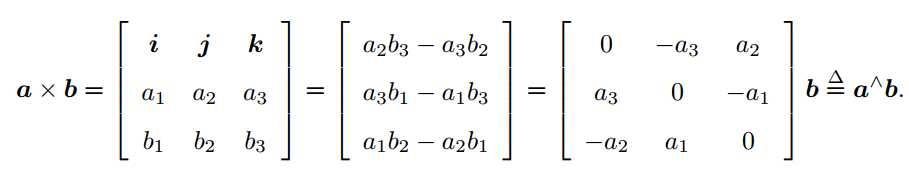
注：可以使用外积表示向量的旋转。

注：^ 记成一个反对称符号。

旋转矩阵

假设某个单位正交基(e1; e2; e3) ，经过一次欧式变换，变成了(e′ 1; e′ 2; e′ 3)，对于同一个向量 a （注意该向量并没有随着坐标系的旋转而发生运动），它在两个坐标系下的坐标为 [a1; a2; a3]T 和 [a′ 1; a′ 2; a′ 3]T：

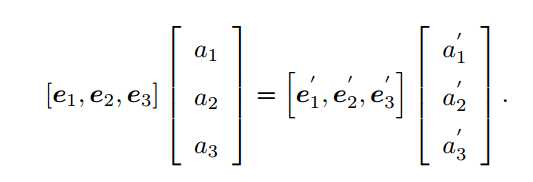
整理可得：

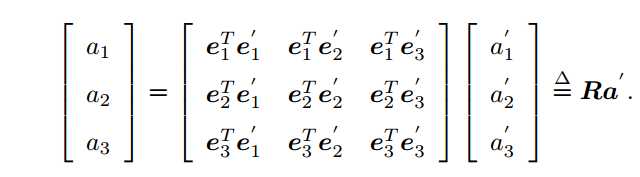
注：旋转矩阵Ｒ是一个行列式为 1 的正交矩阵。反之，行列式为 1 的正交矩阵也是一个旋转矩阵。

• 特殊正交群

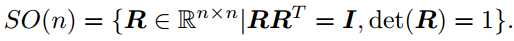
注：SO(n) 是特殊正交群（ Special Orthogonal Group）的意思。

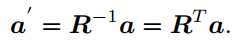
注：R^T 刻画了一个相反的旋转。

变换矩阵和齐次坐标

• 特殊欧式群

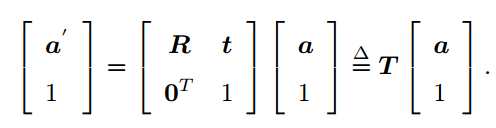
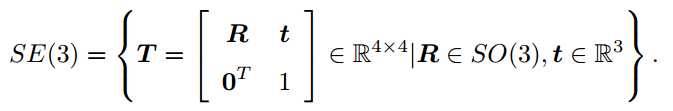
注：变换矩阵Ｔ的逆表示反向的变换

旋转向量

1. SO(3) 的旋转矩阵有九个量，但一次旋转只有三个自由度。因此这种表达方式是冗余的。
2. 旋转矩阵自身带有约束：它必须是个正交矩阵，且行列式为 1。这些约束会使得优化求解变得更困难。

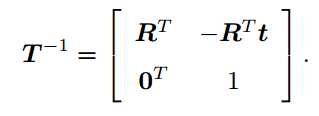
任意旋转都可以用一个旋转轴和一个旋转角来刻画。假设有一个旋转轴为 n，角度为 θ 的旋转，显然，它对应的旋转向量为 θn。由罗德里格斯公式可知：

• 旋转向量－>旋转矩阵

• 旋转矩阵－>旋转向量

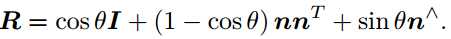
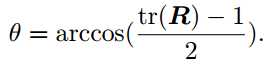
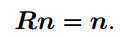
注：转轴 n 是矩阵 R 特征值 1 对应的特征向量。 

欧拉角

欧拉角则提供了一种非常直观的方式来描述旋转——它使用了三个分离的转角，把一个旋转分解成三次绕不同轴的旋转。
假设一个刚体的前方（朝向我们的方向）为X 轴，右侧为 Y 轴，上方为 Z 轴，见图 3-3。那么， ZY X 转角相当于把任意旋转分解成以下三个轴上的转角：

• 绕物体的 Z 轴旋转，得到偏航角 yaw；
• 绕旋转之后的 Y 轴旋转，得到俯仰角 pitch；
• 绕旋转之后的 X 轴旋转，得到滚转角 roll。

注：欧拉角的一个重大缺点是会碰到著名的万向锁问题（ Gimbal Lock）

四元数

四元数是 Hamilton 找到的一种扩展的复数. 它既是紧凑的，也没有奇异性。

一个四元数 q 拥有一个实部和三个虚部。

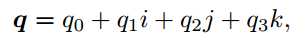
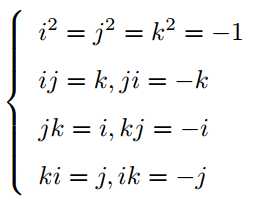
人们也用一个标量和一个向量来表达四元数：

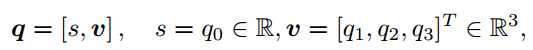
注：我们能用单位四元数表示三维空间中任意一个旋转

四元数与旋转向量的对应关系

• 旋转向量->四元数

• 四元数－>旋转向量

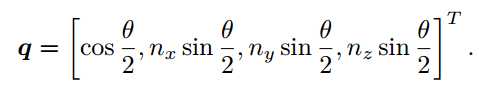
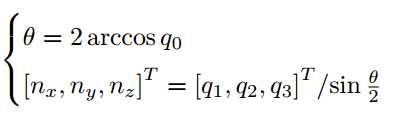
注：在四元数中， 任意的旋转都可以由两个互为相反数的四元数表示。

四元数的运算

1. 加法和减法

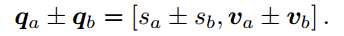
2. 乘法

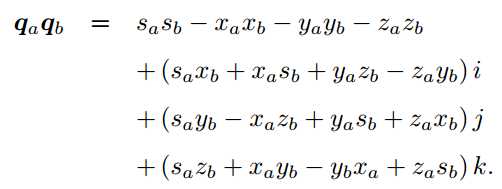
3. 共轭

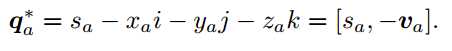
4. 模长

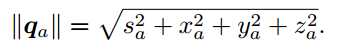
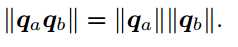
5. 逆

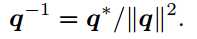
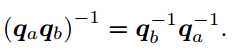
6. 数乘与点乘

用四元数表示旋转

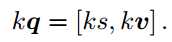
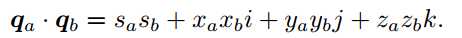
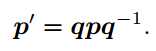
注：p′表示为三维点 p经过四元数 q 旋转后的三维点。

四元数与旋转矩阵的关系

• 四元数->旋转矩阵

• 旋转矩阵->四元数

关于其他几种变换

相似变换

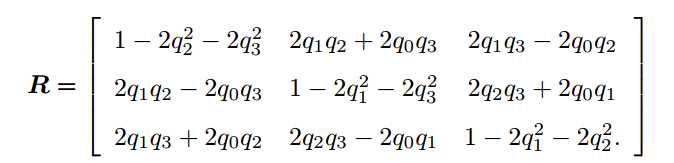
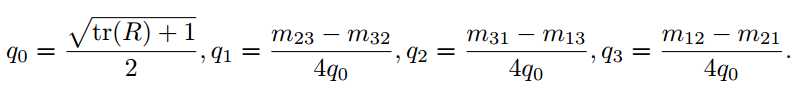
相似变换比欧氏变换多了一个自由度，它允许物体进行均匀的缩放，其矩阵表示为：

仿射变换

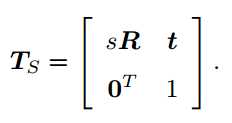
与欧氏变换不同的是，仿射变换只要求 A 是一个可逆矩阵，而不必是正交矩阵。仿射变换也叫正交投影。经过仿射变换之后，立方体就不再是方的了，但是各个面仍然是平行四边形：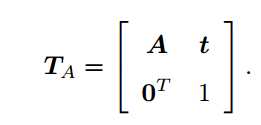

射影变换

射影变换是最一般的变换，它左上角为可逆矩阵 A，右上为平移 t，左下缩放 a^T。2D 的射影变换一共有 8 个自由度， 3D 则共有 15 个自由度。

从真实世界到相机照片的变换可以看成一个射影变换。

《视觉slam十四讲》之第３讲－三维刚体运动

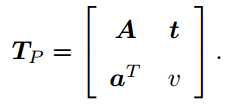
标签：冗余   问题   旋转矩阵   角度   优化   约束   变换   特殊   special   

原文地址：https://www.cnblogs.com/ChrisCoder/p/10029808.html