标签：amp 浮动 特征 数据集 src idt ima 参数估计 三维
一、线性方程
Θ1，Θ2，。。。为参数，Θ0为偏置，x1,x2,...xn为特征
若在二维平面中，一个特征，找出一条最合适的直线去拟合我们的数据
所在三维平面中，两个特征，找出一个最合适的平面去拟合我们的数据。
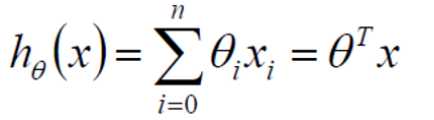
二、误差
真实值和预测值之间肯定存在差异
对每个样本来说：
（1）
误差ε符合：独立，同分布，均值为0，方差为Θ2的高斯分布。
独立：样本之间互相不影响。
同分布：所有样本服从于同一个规律
高斯分布：即正态分布，绝大多数情况下，误差不会太大，极小情况下浮动大，属于正常情况。
三、将ε代入高斯分布
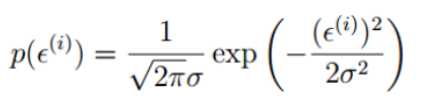（2）
将（1）式代入（2）式
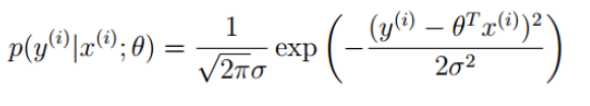
四、似然函数
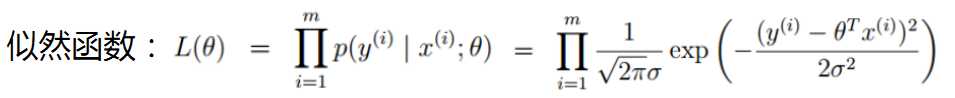
最大似然估计：现在已经拿到了很多个样本（你的数据集中所有因变量），这些样本值已经实现，最大似然估计就是去找到那个（组）参数估计值，使得前面已经实现的样本值发生概率最大。因为你手头上的样本已经实现了，其发生概率最大才符合逻辑。这时是求样本所有观测的联合概率最大化，是个连乘积。
五、对数似然
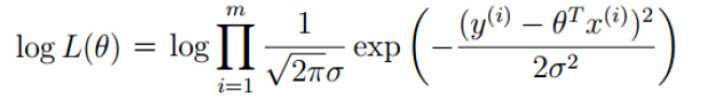
只要取对数，就变成了线性加总。此时通过对参数求导数，并令一阶导数为零，就可以通过解方程（组），得到最大似然估计值。
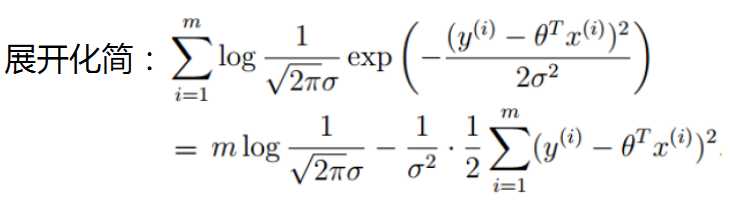
六、最小二乘法
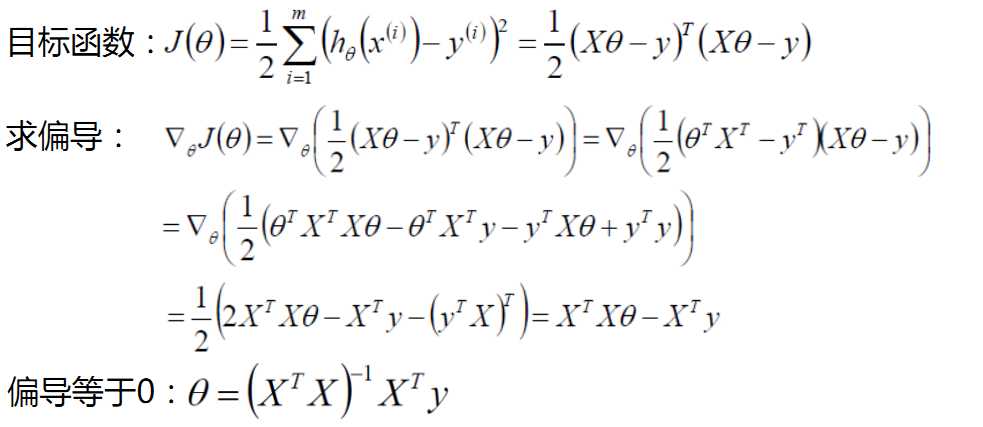
七、评估方法
相关系数R2
R平方：决定系数，反应因变量的全部变异能通过回归关系被自变量解释的比例。如R平方为0.8，则表示回归关系可以解释因变量80%的变异。换句话说，如果我们能控制自变量不变，则因变量的变异程度会减少80%
R平方值=回归平方和(ssreg)/总平方和(sstotal)
其中回归平方和=总平方和-残差平方和(ssresid)
R2越接近于1，我们认为模型拟合的越好
拟合优度越大，自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比高。观察点在回归直线附近越密集。
矩阵知识补充：
矩阵的迹定义如下
一个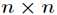
的矩阵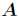
的迹是指
的主对角线上各元素的总和，记作
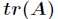。即
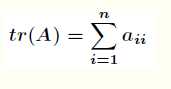
标签：amp 浮动 特征 数据集 src idt ima 参数估计 三维
原文地址：https://www.cnblogs.com/zhangyafei/p/10032215.html
