标签:wiki 接下来 lan 浮点数 flatten 标签 意思 from div
这一章先从最简单的回归开始,也就是基于普通最小二乘的线性回归。f(x)=w0x0+w1x1+w2x2+....。问题就在于求W矩阵。平方误差求导可得:W估计=(X^TX)^-1X^Ty。自写模块代码如下:

1 #!/usr/bin/env python 2 #-*-coding:utf-8 -*- 3 4 from numpy import * 5 import matplotlib.pyplot as plt 6 ‘‘‘ 7 基于普通最小二乘的线性回归 8 ‘‘‘ 9 10 def loadDataSet(fileName): 11 """ 加载数据 12 解析以tab键分隔的文件中的浮点数 13 Returns: 14 dataMat : feature 对应的数据集 15 labelMat : feature 对应的分类标签,即类别标签 16 17 """ 18 # 获取样本特征的总数,不算最后的目标变量 19 numFeat = len(open(fileName).readline().split(‘\t‘)) - 1 20 dataMat = [] 21 labelMat = [] 22 fr = open(fileName) 23 for line in fr.readlines(): 24 # 读取每一行 25 lineArr =[] 26 # 删除一行中以tab分隔的数据前后的空白符号 27 curLine = line.strip().split(‘\t‘) 28 # i 从0到2,不包括2 29 for i in range(numFeat): 30 # 将数据添加到lineArr List中,每一行数据测试数据组成一个行向量 31 lineArr.append(float(curLine[i])) 32 # 将测试数据的输入数据部分存储到dataMat 的List中 33 dataMat.append(lineArr) 34 # 将每一行的最后一个数据,即类别,或者叫目标变量存储到labelMat List中 35 labelMat.append(float(curLine[-1])) 36 return dataMat,labelMat 37 38 39 def standRegres(xArr,yArr): 40 ‘‘‘ 41 Description: 42 线性回归 43 Args: 44 xArr :输入的样本数据,包含每个样本数据的 feature 45 yArr :对应于输入数据的类别标签,也就是每个样本对应的目标变量 46 Returns: 47 ws:回归系数 48 ‘‘‘ 49 50 # mat()函数将xArr,yArr转换为矩阵 mat().T 代表的是对矩阵进行转置操作 51 xMat = mat(xArr) 52 yMat = mat(yArr).T 53 # 矩阵乘法的条件是左矩阵的列数等于右矩阵的行数 54 xTx = xMat.T*xMat 55 # 因为要用到xTx的逆矩阵,所以事先需要确定计算得到的xTx是否可逆,条件是矩阵的行列式不为0 56 # linalg.det() 函数是用来求得矩阵的行列式的,如果矩阵的行列式为0,则这个矩阵是不可逆的,就无法进行接下来的运算 57 if linalg.det(xTx) == 0.0: 58 print("This matrix is singular, cannot do inverse") 59 return 60 # 最小二乘法 61 # http://cwiki.apachecn.org/pages/viewpage.action?pageId=5505133 62 # 书中的公式,求得w的最优解 63 ws = xTx.I * (xMat.T*yMat) 64 return ws 65 66 67 def regression1(): 68 xArr, yArr = loadDataSet("E:\ML_data\data.txt") 69 xMat = mat(xArr) 70 yMat = mat(yArr) 71 ws = standRegres(xArr, yArr) 72 fig = plt.figure() 73 ax = fig.add_subplot(111) #add_subplot(349)函数的参数的意思是,将画布分成3行4列图像画在从左到右从上到下第9块 74 ax.scatter(xMat[:, 1].flatten().A[0], yMat.T[:, 0].flatten().A[0]) #scatter 的x是xMat中的第二列,y是yMat的第一列 75 xCopy = xMat.copy() 76 xCopy.sort(0) # 排序是因为ax.scatter中也排序了 77 yHat = xCopy * ws # 预测出的y值 78 ax.plot(xCopy[:, 1], yHat) 79 plt.show() 80 81 if __name__ == ‘__main__‘: 82 regression1()
这里输入的数据格式:
第一列是x0,第二列是x1,最后一列是y.因为x0都为1,其实y=w0+w1*x1。结果如下:
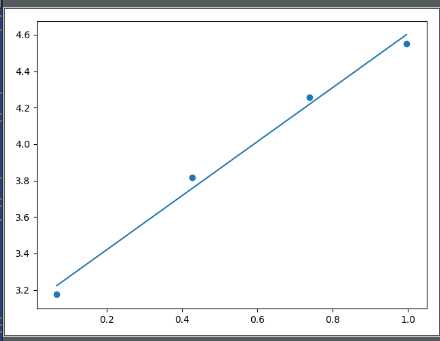
到此最简单线性规划基本结束,但是这种线性规划很容易欠拟合,因为它就是一条直线。故又引出了局部加权线性规划(里面有一个核参数K要调)。
标签:wiki 接下来 lan 浮点数 flatten 标签 意思 from div
原文地址:https://www.cnblogs.com/maxiaonong/p/10037052.html