标签:span 距离 names void lld tchar col lse cout
带修改下,边点都带权的重心
随着变动的过程中,一些子树内的点经过会经过一些公共边。考虑能不能对这样的子树一起统计。
把树上贡献分块。
考虑点分治算法
不妨先把题目简化一下:
假设没有修改,多次询问,每次给定一个s,求$\sum d_v*dis(s,v)$
为了让一块可以一起统计,
我们设:
$sum[x]:$x为根的点分治树管辖部分的权值和
$df[x]$:x为根的点分治树管辖部分到x分治树father的带权距离和$\sum d[v]*dis[v,fa[x]]$
$dm[x]:$ x为根的点分治树管辖部分到x自己的带权距离和
自底向上统计总距离
开始加上$dm[s]$,然后不断加上$dis(s,fa)*(sum[fa]-sum[las])+dm[fa]-df[las]$
las代表上一个father
$dis(s,fa)$可以开始点分治的时候保存(反正就log个)
对于一个s,可以$logn$找到答案
$dm,sum,df$也可以轻而易举$logn$修改
问题是现在我们不知道s是哪一个。
我们比较熟悉一个叫货仓选址问题。
这个重心,很类似于带权中点。
从分治树的root开始,枚举原树上的出边,到y,y所在的这一层的分治树的father叫做son。如果存在一个子树的sum[son]要大于x的剩下分支的点值总和,那么重心一定在son里。
(简单证明:
如果存在sum[son]>sum[x]-sum[son],那么这样的son一定只有一个
存在往son走,减去的代价多,增加的代价少。存在代价更小的情况。(至少是y)
而往其他子树走,代价一定是单调递增上涨的。不可能更优。
所以,重心一定在son管辖的分治树这块区域
)
可以递归处理下去。
但是一个问题是,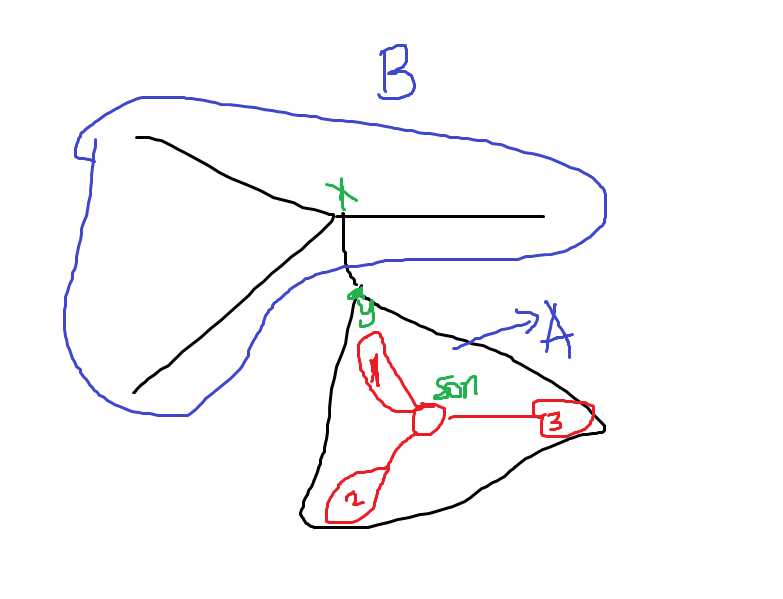
如果到了son位置,但是对于son的1号子树,权值和必须考虑上B的所有权值和。
否则肯定不能直接走。
我们还要返回去考虑father们的权值?
发现难以处理。因为之后的划分可能较多。还要$logn$暴力找father
发现B的权值只有在询问包含y的子树的块才会用到。
所以,我们干脆直接把y点的权值加上sum[B]。回溯回来再减去。
然后就可以放心大胆查询子树的权值和了。
(因为这个小trick瞎写了半天。。。。)
由于只会找到一个son,所以,每次找s的复杂度是:$O(20logn+log^2n)$
就可以了。
(虽然暴力$20*log^2n$每次也可以过,因为时限6s)
代码:
// luogu-judger-enable-o2 #include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^‘0‘) using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch==‘-‘)&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=1e5+5; int n,m; struct node{ int nxt,to; int son; ll val; }e[2*N]; int hd[N],cnt; void add(int x,int y,ll z){ e[++cnt].nxt=hd[x]; e[cnt].to=y; e[cnt].val=z; hd[x]=cnt; } ll has[N]; int rt; ll dm[N],df[N],sum[N]; ll dis[N][20]; int fa[N]; int sz[N],mxsz[N]; int nowsz; int gen; int dep[N]; bool vis[N]; void dfs1(int x,int ff,int d){ dep[x]=d; sz[x]=1;mxsz[x]=0; for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(y==ff) continue; if(vis[y]) continue; dfs1(y,x,d); sz[x]+=sz[y]; mxsz[x]=max(mxsz[x],sz[y]); } mxsz[x]=max(mxsz[x],nowsz-sz[x]); if(mxsz[x]<=nowsz/2){ rt=x; } } void dfs2(int x,int ff,int d){ sz[x]=1; for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(y==ff||vis[y]) continue; dis[y][d]=dis[x][d]+e[i].val; dfs2(y,x,d); sz[x]+=sz[y]; } } int divi(int x,int ff,int d){ rt=0; dfs1(x,0,d); dis[rt][d]=0; fa[rt]=ff; dfs2(rt,0,d); vis[rt]=1; int now=rt; for(reg i=hd[now];i;i=e[i].nxt){ int y=e[i].to; if(vis[y]) continue; nowsz=sz[y]; e[i].son=divi(y,now,d+1); } return now; } void upda(int x,ll c){//c is change int gg=x; int nd=dep[x]; while(x){ sum[x]+=c; df[x]+=c*dis[gg][nd-1]; dm[x]+=c*dis[gg][nd]; x=fa[x]; --nd; } } int query(int x,int d){ //cout<<" querying "<<x<<" || "<<" "<<d<<endl; for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(dep[y]<dep[x]) continue; int lp=e[i].son; if(sum[lp]>sum[x]-sum[lp]){ upda(y,sum[x]-sum[lp]); int ret=query(lp,d+1); upda(y,sum[lp]-sum[x]); return ret; } } return x; } ll calc(int x){ ll ret=dm[x]; int gg=x; int las=x; x=fa[x]; int nd=dep[x]; while(x){ ret+=(dm[x]-df[las])+(sum[x]-sum[las])*dis[gg][nd]; --nd; las=x; x=fa[x]; } return ret; } int main(){ rd(n);rd(m); int x,y; ll z; for(reg i=1;i<=n-1;++i){ rd(x);rd(y);scanf("%lld",&z); add(x,y,z);add(y,x,z); } nowsz=n; gen=divi(1,0,1); //cout<<" ffafaf "<<endl; // for(reg i=1;i<=n;++i){ // cout<<i<<" : "<<fa[i]<<endl; // } //cout<<" gen "<<gen<<endl; while(m--){ rd(x);scanf("%lld",&z); upda(x,z); has[x]+=z;//warning!!!! // for(reg i=1;i<=n;++i){ // cout<<i<<" : "<<sum[i]<<" "<<dm[i]<<" "<<df[i]<<endl; // } int core=query(gen,1); printf("%lld\n",calc(core)); } return 0; } } int main(){ // freopen("data.in","r",stdin); // freopen("my.out","w",stdout); Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/11/29 8:55:17 */
标签:span 距离 names void lld tchar col lse cout
原文地址:https://www.cnblogs.com/Miracevin/p/10038808.html